Непрерывные дроби и перевод рационального числа в конечную дробь

Определение

Непрерывной дробью называют дробь вида

Если эта дробь где-либо заканчивается, её называют конечной непрерывной дробью.

Конечные непрерывные дроби соответствуют рациональным числам.

Пример.

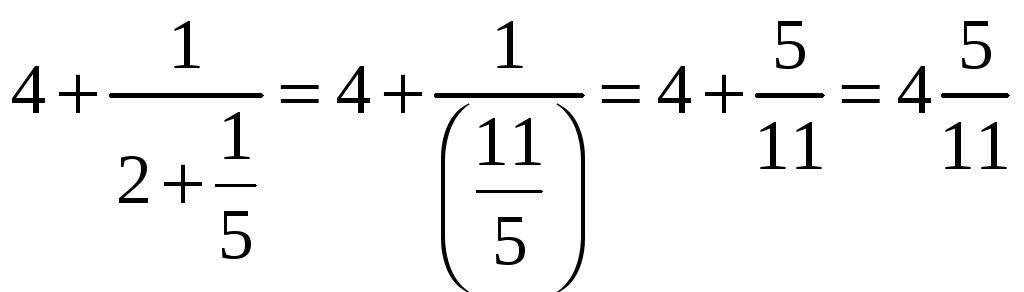
Возможно и обратное действие: получение непрерывной дроби из рационального числа.

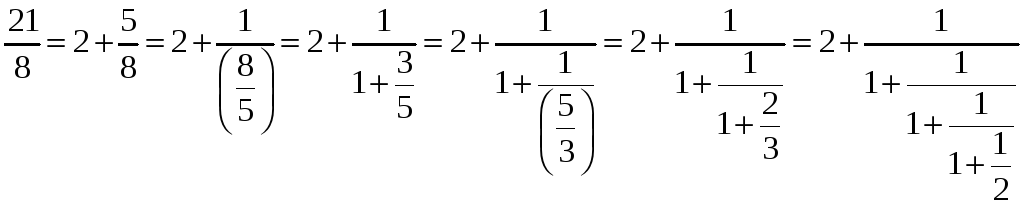
Обычно такую непрерывную дробь записывают в виде (2; 1, 1, 1, 2). Целая часть отделяется точкой с запятой.

Теперь покажем другой способ нахождения коэффициентов непрерывной дроби. Применим алгоритм Евклида к числам 21 и 8.

21 = 8 ∙ 2 + 5

8 = 5 ∙ 1 + 3

5 = 3 ∙ 1 + 2

3 = 2 ∙ 1 + 1

2 = 1 ∙ 2

Обратите внимание на связь коэффициентов непрерывной дроби с неполными частными в алгоритме Евклида!

Если у этой дроби начиная с некоторого места образуется период, её называют периодической непрерывной дробью.

Периодическую непрерывную дробь можно выразить в виде корня некоторого квадратного уравнения.

Пример.

Тогда

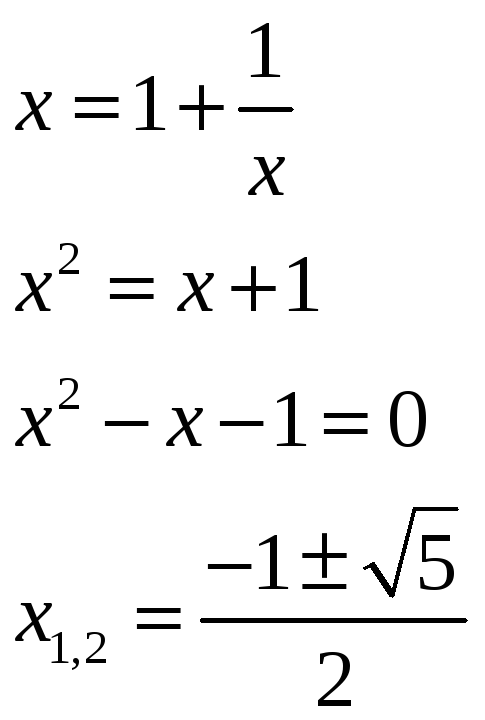
Поскольку число положительное, из двух значений берём положительное.

Можно получить разложение иррационального числа в периодическую дробь следующим способом.

a₀ равно целой части некоторого числа α.

Поэтому

Далее заметим, что a₁ равно целой части числа α₁.

Далее, a₂ равно целой части числа α₂, и так далее, пока не получим цикл, то есть равенство вида α_k = α_n. Это означает, что получен период.

Для чисел, являющихся корнями квадратных уравнений (в том числе для квадратных корней из натуральных чисел) период получится обязательно.

Пример.

Пусть .

Целая часть α равна 1. Поэтому

Целая часть α₁ равна 1.

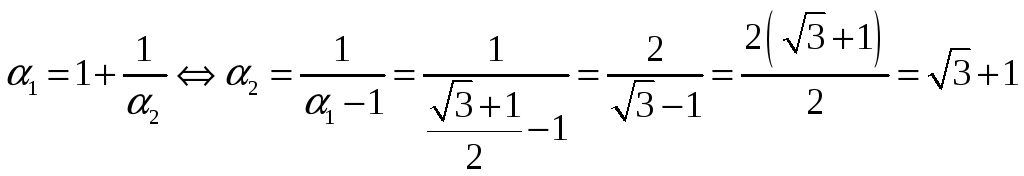
Примечание.

В задачах такого вида целую часть нужно искать именно домножением на сопряжённые, а не на калькуляторе, потому что для больших целых чисел, например, для трёхзначных, может накопиться ошибка округления, и значения целой части найдёте неверно.

Целая часть α₂ равна 2.

Образовался цикл.

Ответ для периодической непрерывной дроби записывают в виде:

При этом целая часть отделена точкой с запятой, а период заключён во внутренние скобки.

Подходящей непрерывной дробью для данного числа α называют непрерывную дробь, которую мы оборвали на одном из коэффициентов. Для вычислений на практике, разумеется, так обычно и поступают.

Наилучшие приближения

На первый взгляд, непрерывные дроби могут показаться всего-навсего искусственно придуманным математическим объектом с неудобной формой записи.

Но приведём формулировку одной теоремы, чтобы стало понятно, где такие дроби можно применить.

Определение.

Наилучшим приближением числа α для дробей со знаменателем, не превышающим данное число n, называют рациональное число со знаменателем, не превышающим n, модуль разности которого с числом α наименьший.

Теорема (без доказательства).

Наилучшим приближением данного вещественного числа является одна из подходящих непрерывных дробей.

Разбор типовых примеров к первому индивидуальному домашнему заданию по теме «Делимость целых чисел и многочленов»

1. Диофантовы уравнения.

Решите диофантово уравнение 903x + 994 y = 14

Сначала найдём наибольший общий делитель коэффициентов в левой части, то есть НОД (903, 994).

Применим алгоритм Евклида.

994 = 903 ∙ 1 + 91

903 = 91 ∙ 9 + 84

91 = 84 ∙ 1 + 7

84 = 7 ∙ 12

Таким образом, НОД (903, 994) = 7.

Разделим обе части уравнения 903x + 994 y = 14 на 7.

Получим 129 x + 142 y = 2.

Найдём пару целых чисел x и y, таких, что 129 x + 142 y = 1.

Для этого воспользуемся обобщённым алгоритмом Евклида.

Сначала найдём НОД (129, 142) (мы уже знаем, что он равен 1, но результаты вычислений понадобятся нам для промежуточных выкладок).

142 = 129 ∙ 1 + 13

129 = 13 ∙ 9 + 12

13 = 12 ∙ 1 + 1

12 = 1 ∙ 12

Теперь эти выкладки рассматриваем от конца к началу, то есть выразим 1 как линейную комбинацию 13 и 12, затем – как линейную комбинацию 129 и 13, и, наконец, как линейную комбинацию 142 и 129.

1 = 13 – 12 = 13 – (129 – 13 ∙ 9) = 13 – 129 + 13 ∙ 9 = 13 ∙ 10 – 129 = (142 - 129) ∙ 10 – 129 = 142 ∙ 10 – 129 ∙11

Итак, мы нашли и такие, что .

Но, поскольку уравнение имеет вид 129 x + 142 y = 2, то два найденных числа умножим на 2, то есть в качестве частного решения возьмём и .

Теперь найдём общее решение. Если в уравнении 129 x + 142 y = 2 величину x уменьшить на 142, а величину y увеличить на 129, то сумма не изменится, поскольку величина 129 ∙ 142 к одному слагаемому прибавляется, а из другого слагаемого вычитается.

Поэтому можем общее решение записать так.

x = -22 – 142 t, y = 20 + 129 t, t – произвольное целое число.

Это и будет ответом.

Ответ. x = -22 – 142 t, y = 20 + 129 t, t – произвольное целое число.

Примечание 1.

Если в условии стоит не сумма, а разность, например, 129 x – 142 y = 2, то величины 142 t и 129 t нужно будет брать с одним знаком, поскольку в этом случае увеличение чисел 129 x и 142 y будет происходить на одно и то же число. Поэтому их разность не изменится.

Примечание 2.

В этой задаче, как и во многих других задачах данной серии, можно проверить свой ответ, подставив числа в исходное уравнение или в уравнение 129 x + 142 y = 2 (если вы уверены, что правильно сократили).

Подставим их.

129(-22 – 142 t) + 142 (20 + 129 t) = 129 ∙ (-22) – 129 ∙ 142 t + 142 ∙ 20 + 142 ∙ 129 t = 129 ∙ (-22) + 142 ∙ 20 = 2.

При этом, если вы не учли примечание 1 и ошиблись со знаками, то при проверке это сразу увидите.

2. Вычислите 3/19 в кольце вычетов по модулю 35.

Сначала найдём 1/19 в кольце вычетов по модулю 35. Обратите внимание, что мы практически должны вычислить дробь для выражения с целыми числами!

Запишем формулировку задачи так.

x = 1/19 (mod 35)

И, наконец: найти целые числа x и y такие, что:

(причём x должен быть одним из остатков при делении на 35, то есть лежать в пределах от 0 до 34 включительно).

Подобную задачу мы уже решали – это диофантово уравнение, только достаточно получить одну пару целых чисел, удовлетворяющую условию, а затем заменить полученный x остатком от его деления на 35.

Применим сначала алгоритм Евклида для чисел 19 и 35, затем обобщённый алгоритм Евклида.

35 = 19 ∙ 1 + 16

19 = 16 ∙ 1 + 3

16 = 3 ∙ 5 + 1

3 = 1 ∙ 3

Теперь выразим 1 = НОД (19, 35) в виде линейной комбинации чисел 19 и 35.

1 = 16 – 3 ∙ 5 = 16 – (19 – 16) ∙ 5 = 16 ∙ 6 – 19 ∙ 5 = (35 – 19) ∙ 6 – 19 ∙ 5 = 35 ∙ 6 – 19 ∙ 11.

Итак, при поиске решения уравнения мы получили x = -11.

Поскольку x должен быть одним из остатков при делении на 35, мы должны заменить -11 остатком от деления на 35. Тогда получим число 24. Это число равно 1/19 в кольце вычетов по модулю 35.

Наконец, вспомним, что мы искали значение 3/19. Для этого умножим число 24 на 3 и разделим результат на 35 с остатком. Получим число 2.

Ответ: 2.

Примечание.

Ответ в этой задаче легко проверить. В самом деле, если мы умножим число 2 на 19, получим число 38, что сравнимо с 3 по модулю 35. То есть 19 x ≡ 3 (mod 35), а, значит,

x = 3/19 в кольце вычетов по модулю 35.

3. Китайская теорема об остатках.

Найти наименьшее натуральное число, которое при делении на 3 даёт остаток 2, при делении на 5 остаток 3, при делении на 7 остаток 2.

Представим искомое число в виде суммы трёх чисел:

одно кратно 5 и 7 и даёт остаток 2 при делении на 3 (поскольку сравнение имеет решение, похожее сравнение было разобрано в задаче 2),

второе кратно 3 и 5 и даёт остаток 2 при делении на 7 (по аналогичной причине),

третье кратно 7 и 3 и даёт остаток 3 при делении на 5.

Первое число будет равно 35, второе равно 30, третье равно 63. Сумма этих чисел равна 128.

Обратите внимание, что это не наименьшее число, дающее требуемые остатки, что не удивительно, при вычислениях мы использовали только величины остатков.

Чтобы получить минимальное число, нужно разделить наш промежуточный результат 128 на произведение чисел 3, 5 и 7, то есть на число 105. Остаток равен 23, это и есть ответ. Проверьте, что он действительно даёт требуемые остатки.

Ответ: 23.

Примечание. Именно в такой формулировке, с этими числами, была разобрана эта задача в самом древнем из дошедших до нас источников – китайском сочинении III века н.э. Поэтому соответствующая теорема называется китайской теоремой об остатках.

4. Системы счисления.

Решите уравнение, записанное в 9-ичной системе счисления.

5x + 120 = 532

Решение запишите в 9-ичной и десятичной системах счисления.

(Это означает, например, что 500 в 9-ичной системе равно , поскольку число 9 в 9-ичной системе играет ту же роль, что число 10 в десятичной системе счисления).

Далее вычисляем в десятичной системе.

5x = 434 – 99 = 335

x = 335 : 5 = 67 (в десятичной системе).

x =

Ответ:

5. Найти представление рационального числа 343/155 непрерывной дробью.

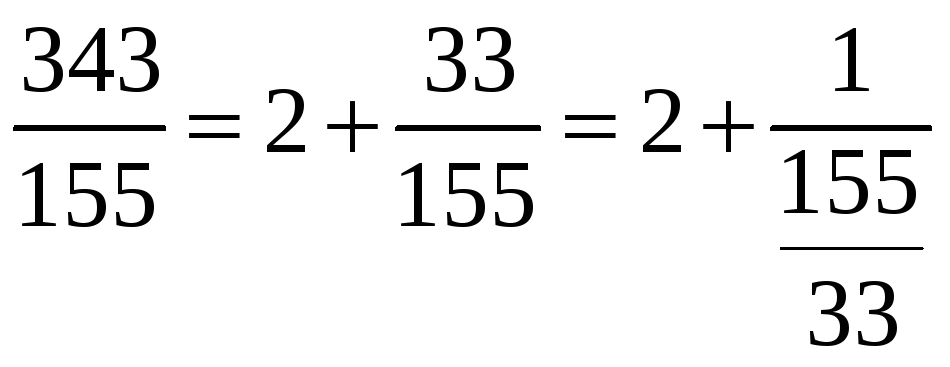
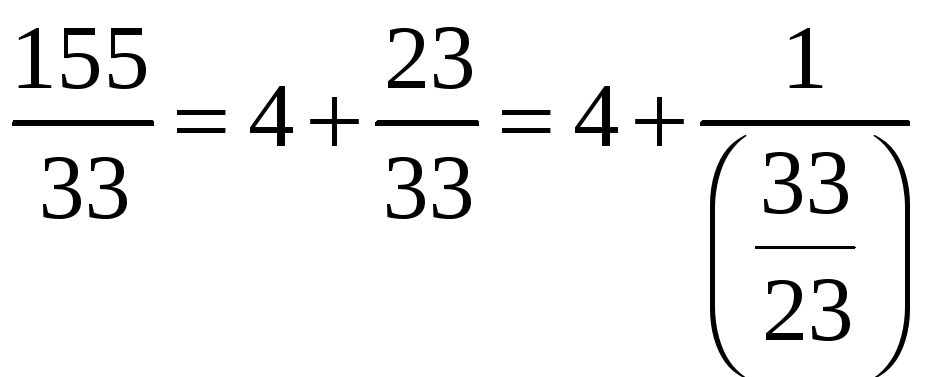
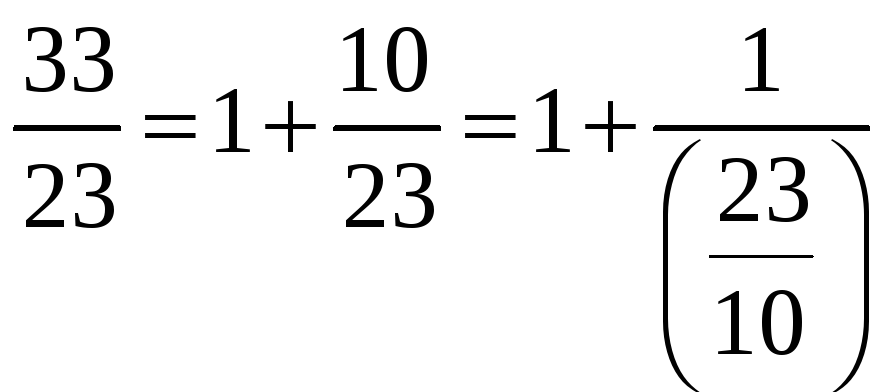
Как только в знаменателе получили целое число, можем собрать все результаты в одну многоэтажную дробь.

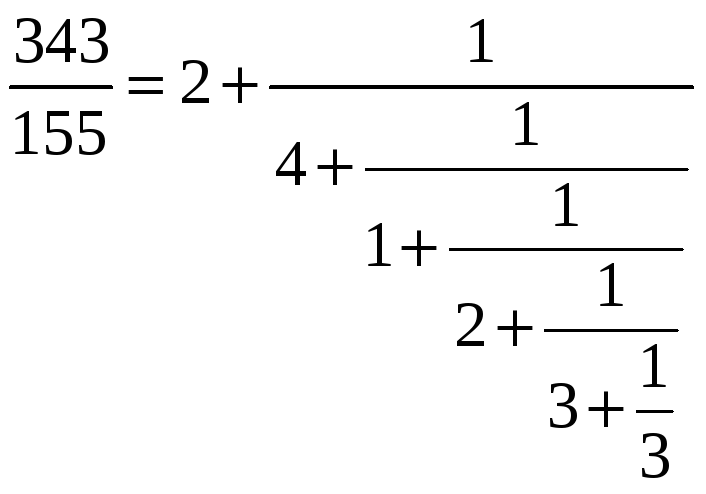
Обычно такой ответ записывают в виде: (2; 4, 1, 2, 3, 3).

Техника вычислений (в предисловии: указать рекомендации, что считать вручную, а что на калькуляторе или компьютере, а также рекомендации о разделении материала на лекции и семинары).

Материалы для семинаров (для обязательного решения предлагаются задачи с номерами 1, 7, 8, 9, 10, остальные задачи приведены в качестве дополнительного материала)

ОТВЕТЫ ДЛЯ САМОКОНТРОЛЯ

Комбинаторика

Задачи комбинаторики.

1. Найти количество объектов, удовлетворяющих некоторым условиям.

2. Занумеровать их и построить алгоритм нахождения элемента по номеру и номера по элементу.

Правило произведения

Если А содержит n элементов, множество В содержит m элементов, то множество пар вида (a_i, b_j), где a_i  А, b_j  B, содержит mn элементов.

Пример

Сколько способов поставить две шахматные ладьи на доску 8х8 так, чтобы они не «били» друг друга?

Решение.

Есть 64 способа поставить первую ладью, и на каждый из них приходится по 49 способов поставить вторую ладью (поскольку первая ладья занимает одну клетку, и бьёт при этом 14 клеток, то остаётся 49 клеток для второй ладьи). Таким образом, получим 64  49 вариантов расстановки двух ладей.

Но при этом каждую расстановку при таком подсчёте мы сосчитаем дважды, поскольку могли бы начать с первой ладьи, а могли бы со второй. Поэтому найденное количество нужно разделить на 2.

64  49 / 2 = 1568.

Ответ. 1568.

Пример 2

Сколько существует трёхзначных чисел, у которых все цифры различны?

Решение. Для первой цифры 9 вариантов, от 1 до 9. Когда её выбрали, для второй цифры тоже 9 вариантов, поскольку она не должна совпасть с первой. Когда выбрали первые две цифры, то для третьей осталось 8 вариантов.

По правилу произведения получим ответ: .

Ответ: 648.