Решение уравнений в кольце остатков по данному модулю

Сравнение всегда имеет решение, если числа a и b взаимно просты.

Это следует из того, что выражение ax-by = 1 – это линейное представление наибольшего общего делителя a и b.

Такую задачу иногда формулируют в виде: найти 1/a в кольце вычетов по модулю b. В самом деле, выражение ax = 1 означает по сути то же самое, что x = 1/a (x – искомая величина).

В некоторых случаях вычисляют c/a в кольце вычетов по модулю b. В этом случае сначала можно вычислить 1/a, затем умножить результат на c в кольце вычетов по модулю b.

Уточняем, что умножить число в кольце вычетов по модулю b означает сначала умножить число, затем заменить результат его остатком от деления на b.

Пример

Можно решить уравнение 7x = 1 в кольце вычетов по модулю 9, то есть провести вычисление 1/7 в Z₉.

В данном случае обозначим неизвестную величину как х.

Тогда x = 1/7 в Z₉ 

7x  1 (mod 9) 

7x – 1 9 

7x – 1 = 9y 

7x – 9y = 1

Мы получили уже знакомую нам ситуацию – линейное диофантово уравнение.

Можем его решить, но для первоначальной задачи достаточно найти всего одно значение х – например, подойдёт x = 4. Заметим, что это число находится в пределах от 0 до 8, поэтому может быть остатком при делении на 9.

Итак, ответ: x = 4.

Примечание. Ответ легко проверить умножением: 4 х 7 при делении на 9 даёт остаток 1.

Если бы мы искали, например, 5/7 в Z₉, то сначала нашли бы сначала 1/7 в Z₉ (получив число 4), а затем домножили бы это число на 5 и взяли бы остаток при делении на 9 (остаток от деления 20 на 9 равен 2).

В этом случае ответ был бы равен 2.

Примечание. В задачах на нахождение выражений вида a/b в кольце вычетов по модулю c ответ всегда единственный, и является целым числом, находящимся в пределах от 0 до (c - 1).

В некоторых случаях деление невозможно, поскольку не каждое диофантово уравнение имеет решение. Например, уравнение 4x  1 (mod 10) не имеет решений, поскольку 4x – чётное число, и при делении на 10 остаток будет чётным.

Китайская теорема об остатках (теория)

Пусть - попарно взаимно простые модули (то есть каждые два взаимно просты между собой), – остатки. Тогда существует такой x, что

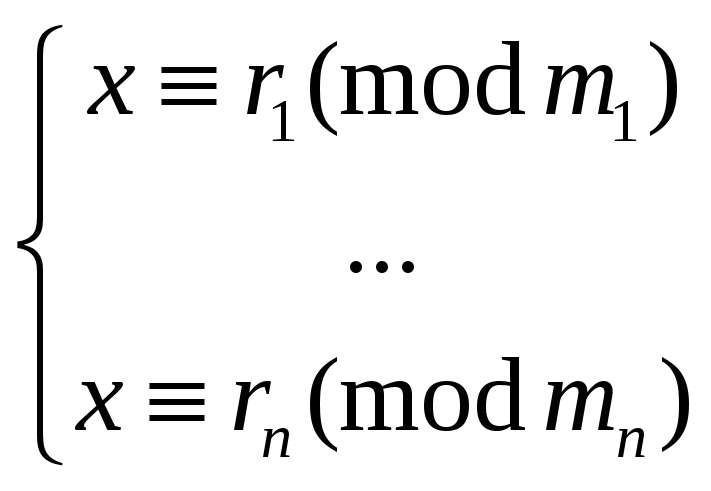
Вообще говоря, такой x не единственный, поскольку от прибавления к нему величины остатки по модулю останутся теми же.

Но если поставить дополнительное условие , то такой x существует и единственный.

Примечание.

То, что модули попарно взаимно просты – существенная деталь. Например, предположим, что . Тогда искомое число должно быть одновременно и чётным, и нечётным, что невозможно.

Сначала, для примера, предположим, что у нас два модуля: .

Тогда представим искомое число в виде суммы двух чисел: одно даёт остаток 1 при делении на 4 и кратно 7, а другое даёт остаток 3 при делении на 7 и кратно 4.

Тогда сумма этих чисел даст искомые остатки.

В качестве первого числа можем взять 21, в качестве второго числа 24. Сложив эти числа, получим 45.

Поскольку для единственности решения поставлено условие , заменим число 45 его остатком от деления на 28, то есть числом 17.

Можно проверить, что оно действительно даёт указанные остатки при делении на 4 и на 7.

Теперь - построение решения для китайской теоремы об остатках в общем виде.

Здесь будем строить его похожим образом, то есть в виде суммы n слагаемых, каждое из которых даёт требуемый остаток по своему модулю, и при этом делится на остальные модули.

Первое слагаемое обеспечит остаток по первому модулю, второе – по второму, и так далее.

Обозначим .

Из условия теоремы вытекает, что НОД

Следовательно, для каждого i существует d_i такое, что .

Найти такое d_i можно, если решить сравнение

(иначе говоря, найти частное решение диофантова уравнения).

Итак, для каждого I выполнено условие . Поэтому .

Тогда число – искомое. Имеется в виду, что мы возьмём остаток от деления данного числа на произведение .

В самом деле, это число:

даёт остаток r₁ при делении на m₁ (поскольку первое слагаемое даёт указанный остаток, а остальные слагаемые делятся на m₁),

даёт остаток r₂ при делении на m₂ (поскольку первое слагаемое даёт указанный остаток, а остальные слагаемые делятся на m₂),

и так далее.