
Умножение вектора на число
Пример 1.8. На плоскости задан вектор![]() (рис. 1.10), изобразите следующие векторы
(рис. 1.10), изобразите следующие векторы![]() ,
,![]() ,
,![]() .
.
Р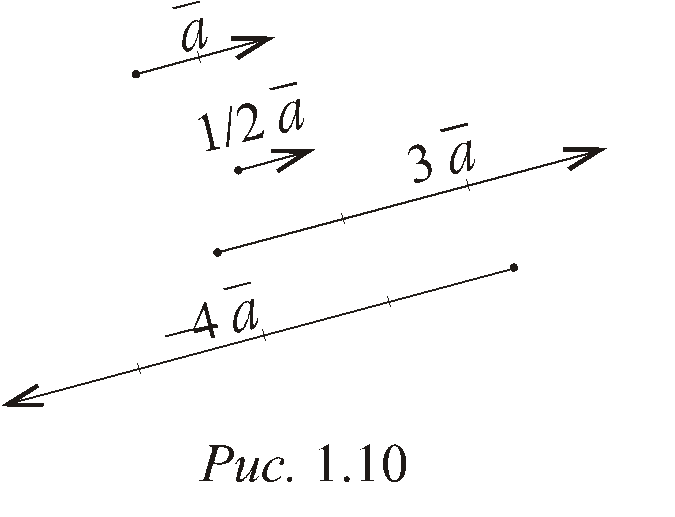 ешение.При умножении вектора
ешение.При умножении вектора![]() на скаляр (число)kполучается вектор
на скаляр (число)kполучается вектор![]() ,
модуль которого равен произведению
модуляaна числоk,т.е.
,
модуль которого равен произведению
модуляaна числоk,т.е.![]() .
Направления векторов
.
Направления векторов![]() и
и![]() совпадают, еслиk > 0, и они
противоположны, еслиk < 0. Обозначение:
совпадают, еслиk > 0, и они
противоположны, еслиk < 0. Обозначение:![]() .
Исходя из этого правила, изображены на
рис. 1.10 векторы
.
Исходя из этого правила, изображены на
рис. 1.10 векторы![]() ,
,![]() ,
,![]() .
.
Пример 1.9. В пространстве задан
вектор![]() (1, 2, –2), найдите следующие векторы: а)
(1, 2, –2), найдите следующие векторы: а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение. При умножении вектора![]() (x,y,z) на числоkполучается вектор
(x,y,z) на числоkполучается вектор![]() (kx,ky,kz),
т.е. при умножении вектора на число
каждая его координата умножается на
это число. Таким образом, координаты
векторов равны: а)
(kx,ky,kz),
т.е. при умножении вектора на число
каждая его координата умножается на
это число. Таким образом, координаты
векторов равны: а)![]() (3,
6, –6); б)
(3,
6, –6); б)![]() (–4, –8, 8); в)
(–4, –8, 8); в)![]() (
(![]() ).
).
Пример 1.10. При каких значенияхmвекторы![]() (1,
3,m) и
(1,
3,m) и![]() (2m, –12,
8) коллинеарны?
(2m, –12,
8) коллинеарны?
Решение. Векторы называются
коллинеарными, если они лежат на одной
или на параллельных прямых. Если при
этом векторы направлены одинаково, то
они называются сонаправленными, а если
противоположно, то противоположно
направленными. Два вектора являются
коллинеарными тогда и только тогда,
когда один из них является произведением
другого на число, или, другими словами,
их координаты пропорциональны. На
математическом языке это записывается
так:![]() .
При
.
При![]() (1, 3,m)
и
(1, 3,m)
и![]() (2m, –12, 8)
можно записать, что
(2m, –12, 8)
можно записать, что![]()
![]()
Ответ:
![]() .
.
Сумма векторов
Сложение векторных величин производится по правилу параллелограмма или по правилу треугольника (рис 1.11).
П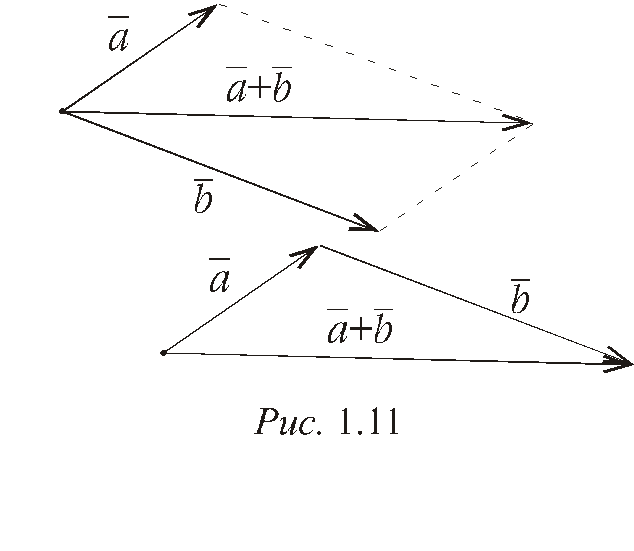 равило
параллелограмма:Сумма двух векторов
равило
параллелограмма:Сумма двух векторов![]() и
и![]() ,
приведенных к общему началу, есть третий
вектор, длина которого равна длине
диагонали параллелограмма, построенного
на векторах
,
приведенных к общему началу, есть третий
вектор, длина которого равна длине
диагонали параллелограмма, построенного
на векторах![]() и
и![]() ,
он направлен от точки общего начала
данных векторов.
,
он направлен от точки общего начала
данных векторов.
Правило треугольника: Сумма двух
векторов![]() и
и![]() ,
если конец первого совпадает с началом
второго, есть третий вектор, длина
которого равна длине третьей стороны
треугольника, построенного на векторах
,
если конец первого совпадает с началом
второго, есть третий вектор, длина
которого равна длине третьей стороны
треугольника, построенного на векторах![]() и
и![]() ,
причем направлен он от начала первого
в конец второго вектора (рис. 1.11).
,
причем направлен он от начала первого
в конец второго вектора (рис. 1.11).
Пример 1.11. На плоскости заданы
векторы (рис. 1.12), изобразите следующие
векторы: а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
Р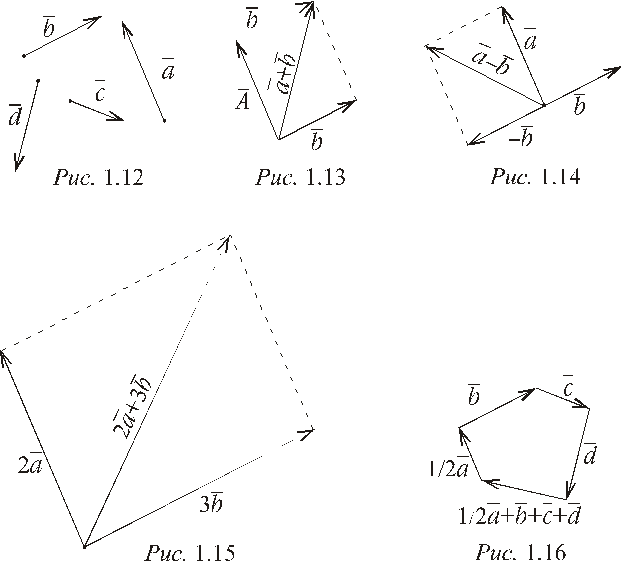 ешение:
ешение:
а) Для построения вектора
![]() можно воспользоваться как правилом
параллелограмма, так и правилом
треугольника (рис. 1.13).
можно воспользоваться как правилом
параллелограмма, так и правилом
треугольника (рис. 1.13).
б) Разность двух векторов
![]() и
и![]() – это вектор, равный сумме векторов
– это вектор, равный сумме векторов![]() и
и![]() ,
где
,
где![]() – вектор, противоположный к вектору
– вектор, противоположный к вектору![]() (рис. 1.14).
(рис. 1.14).
в) Для построения вектора
![]() необходимо воспользоваться определением
умножения вектора на число и каким-либо
правилом сложения векторов (рис. 1.15).
необходимо воспользоваться определением
умножения вектора на число и каким-либо
правилом сложения векторов (рис. 1.15).
г) Сумму нескольких векторов строят
так: берут произвольную точку Oплоскости и из нее строят вектор![]() ,
равный первому слагаемому; из точкиАпроводят вектор
,
равный первому слагаемому; из точкиАпроводят вектор![]() ,
равный второму слагаемому, из точкиВ– вектор
,
равный второму слагаемому, из точкиВ– вектор![]() ,
равный третьему слагаемому и т.д. Наконец,
строят последний вектор с концом в точкеD, вектор
,
равный третьему слагаемому и т.д. Наконец,
строят последний вектор с концом в точкеD, вектор![]() ,
замыкающий полученную ломаную линию,
и будет искомой суммой (рис. 1.16).
,
замыкающий полученную ломаную линию,
и будет искомой суммой (рис. 1.16).
Пример 1.12. В пространстве заданы
векторы![]() (1, 2, –2) и
(1, 2, –2) и![]() (–3, 5, 1), найдите следующие векторы: а)
(–3, 5, 1), найдите следующие векторы: а)![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Решение. При сложении (вычитании)
векторов соответствующие их координаты
складываются (вычитаются). Таким образом,
координаты векторов равны: а)![]() (–2, 7, –1); б)
(–2, 7, –1); б)![]() (4, –3, –3); в)
(4, –3, –3); в)![]() (1, 17/3, –11/3).
(1, 17/3, –11/3).
Пример 1.13. Разложите в плоскости
вектор![]() (1; 2) по базису.
(1; 2) по базису.
Р ешение.В качестве базисных векторов на
плоскости рассматривают
ешение.В качестве базисных векторов на
плоскости рассматривают![]() и
и![]() – векторы, по модулю равные единице и
направленные по координатным осямOxиOy. Тогда видим, что
– векторы, по модулю равные единице и
направленные по координатным осямOxиOy. Тогда видим, что![]() (рис. 1. 17). Действительно, ведь координаты
вектора – это и есть коэффициенты в
разложении вектора по базису.
(рис. 1. 17). Действительно, ведь координаты
вектора – это и есть коэффициенты в
разложении вектора по базису.
В трехмерном случае рассматриваются
базисные векторы
![]() ,
,![]() ,
,![]() .
Можно говорить о том, что записи
.
Можно говорить о том, что записи![]() (x, y,
z) и
(x, y,
z) и![]() равнозначны, в дальнейшем будем
пользоваться обеими этими записями.
равнозначны, в дальнейшем будем
пользоваться обеими этими записями.
Пример 1.14. Найдите![]() и
и![]() ,
если известно, что векторы
,
если известно, что векторы![]() и
и![]() коллинеарны.
коллинеарны.
Решение.В условии задачи векторы
записаны в разложении по базису
пространства, в другой записи имеем:![]() (, 7, 3),
(, 7, 3),![]() (1,, 2). Векторы
коллинеарны, если их координаты
пропорциональны, т. е.
(1,, 2). Векторы
коллинеарны, если их координаты
пропорциональны, т. е.![]() .
Следовательно,=
3/2,= 14/3.
.
Следовательно,=
3/2,= 14/3.
Ответ: = 3/2,= 14/3.
