1.7.1. Свойства векторного произведения

1).

2). , т.е. векторное произведение антикоммутативно.

3). , т.е. векторное произведение обладает распределительным свойством.

4).

1.7.2. Координатная форма записи векторного произведения

Коротко векторное произведение записывается в виде определителя 3-го порядка:

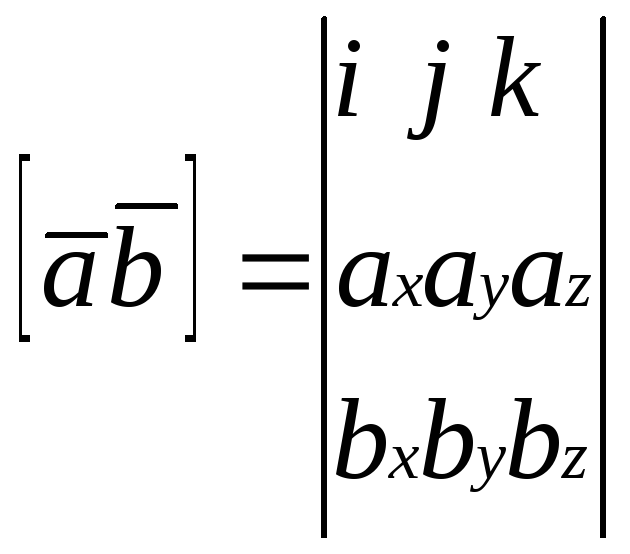, (1.7.2.1)

где - координаты векторав прямоугольной системе координатOxyz(т.е. проекции векторана координатные осиOx, Oy, Oz);- координаты вектора.

Координаты векторного произведения в прямоугольной системе координат можно найти разложив определитель (1.7.2.1) по элементам первой строки с учетом векторного произведения ортов :

,

(1.7.2.2)

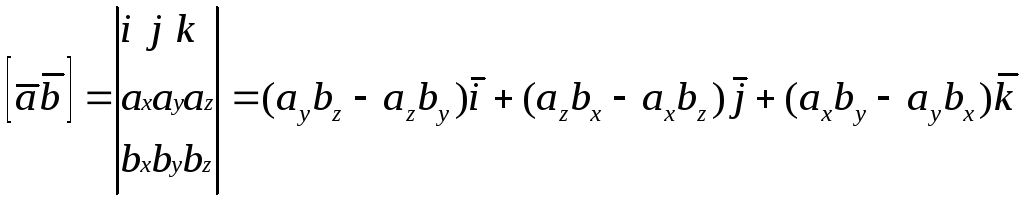
(1.7.2.3)

1.8. Смешанное (векторно - скалярное) произведение векторов

Смешанным произведением трех векторов ,и. называется произведение вида

, (1.8.1)

где первых два вектора перемножаются векторно, а их произведение умножается скалярно на третий вектор .

Смешанное произведение трех векторов - величина скалярная.

Абсолютная величина смешанного произведения некомпланарных векторов ,иравна объемуVпараллелепипеда, построенного на этих векторах, а знак его зависит от ориентации этих векторов: если векторы,иобразуют правую тройку, то их смешанное произведение будет положительно; для левой же тройки произведение - отрицательно.

1.8.1. Свойства смешанного произведения

1. Смешанное произведение не изменяется:

а). Если перемножаемые вектора переставлять в круговом порядке:

б). Если поменять местами знаки векторного и скалярного умножения:

Это позволяет записывать смешанное произведение трех векторов в виде без знаков векторного и скалярного умножения.

2. Перестановка в смешанном произведении любых двух векторов изменяет лишь его знак:

,,.

Действительно, используя равенства

;

имеем:

3. Смешанное произведение обращается в нуль, если:

а). Хотя бы один из перемножаемых векторов ест нуль - вектор,

б). Два из перемножаемых векторов коллинеарны,

в). Три перемножаемых вектора компланарны.

1.8.2. Координатная форма записи смешанного произведения

Коротко смешанное произведение записывается в виде определителя третьего порядка:

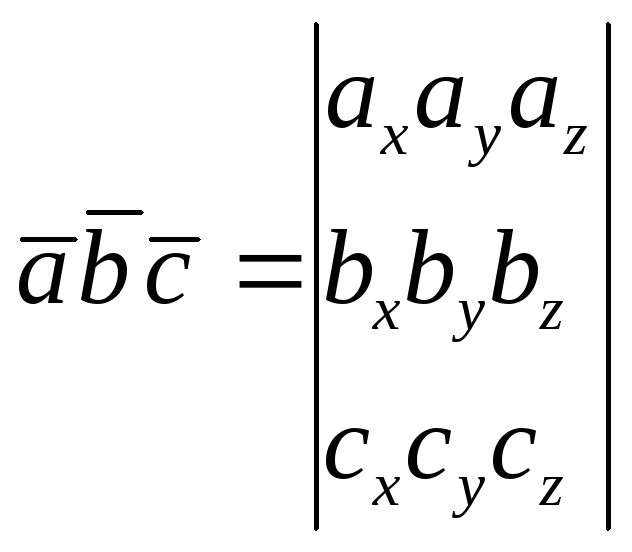(1.8.2.1)

Замечание 1. При помощи смешанного произведения можно вычислить объем четырехгранной пирамиды, заданной координатами ее вершин:

Замечание 2. Три вектора,,компланарны тогда и только тогда, когда их смешанное произведение равно 0.

или

1.9. Двойное векторное произведение трех векторов

Двойным векторным произведением трех векторов называется произведение вида:

(1.9.1)

Так как оно часто используется в приложениях, покажем, что его вычисление можно свести к вычислению более простого выражения, т.е. справедливы следующие равенства:

(1.9.2)

Прежде всего отметим, что двойное векторное произведение трех векторов

есть вектор, компланарный с векторамии.

1.10. Вопросы для самопроверки

1. Дайте определение понятия вектора.

2. Какие векторы называются коллинеарными, компланарными?

3. Основные операции над векторами.

4. Что называется проекцией вектора на заданную ось? Свойство проекций.

5. Дайте определение декартовой прямоугольной системы координат. Векторы в декартовой системе координат.

6. Какая система координат называется полярной? Связь прямоугольных и полярных координат.

7. Запишите операции сложения и умножения вектора на число в координатной форме.

8. Скалярное произведение двух векторов. Определение.

9. Свойства скалярного произведения.

10. Координатная форма записи скалярного произведения.

11. Условия коллинеарности и перпендикулярности векторов. Определение. Свойства.

12. Векторное произведение двух векторов. Определение. Свойства.

13. Координатная форма записи векторного произведения.

14. Смешанное произведение. Свойства.

15. Понятие двойного векторного произведения трех векторов.

13