Матрица разрезов.

Рассмотрим орграф . Если – непустое подмножество множества, то множество дуг, соединяющих вершины, является разрезом, обозначаемым. Ориентациюможно принять как от вершинык вершине, так и наоборот. Допустим, мы принимаем ориентацию от вершинык вершине. Тогда говорят, что ориентация дуги изсоответствует ориентации разреза, если дуга ориентирована от вершины изв вершину из.

Матрица разрезов графа сm ребрами имеет m столбцов и столько строк, сколько в этом графе имеется разрезов. Элемент определяется следующим образом.

Если граф ориентированный,

Если граф неориентированный,

Строки матрицы называютсявекторами разрезов.

Цикломатическая матрица.

Цикл в графе можно обойти в одном из двух направлений: по часовой или против часовой стрелки. Направление, выбираемое для обхода цикла, определяет его ориентацию.

Рассмотрим дугу e с концевыми вершинами к и входит в циклC. Будем говорить, что ориентация дуги e соответствует ориентации цикла, если вершина встречается при обходе циклаC в направлении, указанном его ориентацией, раньше вершины .Цикломатическая матрица графа G с m ребрами имеет m и столько строк, сколько циклов имеется в графе G. Элемент 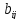определяется следующим образом :

Если граф ориентированный,

Если граф неориентированный,

Матрица Кирхгофа.

Дан простой граф свершинами. Тогда матрица Кирхгофаданного графа будет определяться следующим образом:

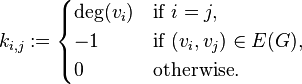
Также матрицу Кирхгофа можно определить как разность матриц

где — это матрица смежности данного графа, а— матрица, на главной диагонали которой степени вершин графа, а остальные элементы — нули:

Если граф является взвешенным, то определение матрицы Кирхгофа обобщается. В этом случае элементами главной диагонали матрицы Кирхгофа будут суммы весов рёбер, инцидентных соответствующей вершине. Для смежных (связанных) вершин , где— это вес (проводимость) ребра. Для различных несмежных (несвязанных) вершин полагается.

Для взвешенного графа матрица смежности записывается с учетом проводимостей ребер, а на главной диагонали матрицыбудут суммы проводимостей ребер инцидентных соответствующим вершинам.

Пример матрицы Кирхгофа.

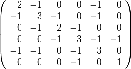
Специальные свойства графов.

Пусть G — произвольный (n,m)-граф с k компонентами связности. Если G — не лес, то в нем (его компонентах связности) существуют циклы. Рассмотрим какой-либо цикл и удалим из него некоторое ребро. При этом количество компонент связности не увеличится. Если после этого еще останутся циклы, то рассмотрим следующий из них и снова удалим какое-либо его ребро. Продолжим этот процесс до тех пор, пока не исчезнут все циклы. Полученный в результате подграф, который, очевидно, является лесом и имеет столько же компонент связности, как и исходный граф G, называется остовом графа G.

Теорема.  Число ребер графа G, которые нужно удалить для получения остова, не зависит от способа удаления и равно m-n+k.

Теорема (Кирхгоф). Число остовов в связном графе G порядка n>=2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа K(G) графа G.

Теорема. Орграф сильно связен, если в нем существует основной циклический маршрут.