Лекции

3.4. Способы передачи информации в цифровых устройствах.

Передача информация в цифровых устройствах осуществляется в последователь-

ном или параллельном коде.

При использовании последовательного кода каждый такт соответствует одному разряду двоичного кода. Номер разряда определяется номером такта, отсчитываемого от такта, совпадающего с началом представления кода. Временные диаграммы, показанные на рисунке 4.3.1, иллюстрируют последовательный код двоичного числа 11001001 при потенциальном и импульсном способе представления информации.

При потенциальном способе (рис. 4.3.1 а) сигнал сохраняет низкий или высокий уровень в течение одного или нескольких тактов. При импульсном способе представления цифровой информации (рис. 4.3.1 б) единичному и нулевому значению двоичной переменной соответствует наличие или отсутствие импульса конечной длительности. Для передачи всего числа требуется восемь тактов.

Параллельный код позволяет существенно сократить время обработки я передачи информации. Для примера, рисунок 4.4.1 иллюстрирует параллельный код семиразрядного числа 1101101. В этом случае, как при импульсном (рис. 4.4.1 а) так и при потенциальном (рис. 4.4.1 б) способе представления информации все разряды двоичного кода представлены в одном временном такте и передаются по раздельным каналам.

Рис.4.4.1. Параллельный код двоичного числа при потенциальном и импульсном способах представления информации

3.5. Элементарные логические функции и элементы.

Как уже было сказано, для n логических аргументов какой-либо логической функции существует 2n их комбинаций. На каждом таком наборе может быть определено значение функции 0 или 1. Если значения функции отличаются хотя бы на одном наборе,

функции – разные. Тогда общее число логических функций от n аргументов равно N 2 2 n . Так для n=2, N=16. Практическое значение имеют, прежде всего, следующие три функции от 2-х переменных.

Логическое отрицание (функция НЕ). Логическим отрицанием переменной х называется такая ЛФ f(x), которая имеет значение 1, когда x = 0 и значение 0, когда х=1. ЛФ НЕ обозначается в виде x . Табл. 4.5.1 представляет собой таблицу истинности логической функции НЕ:

Табл. 4.5.1 Функция НЕ

Функцию НЕ выполняет физический элемент (электронная схема), который называется «элементом НЕ» или инвертором. Обозначение инвертора на функциональных схемах показано на рис. 4.5.1

f

t

Рис.4.5.1. Обозначение и временная диаграмма инвертора

Логическое умножение (конъюнкция). Конъюнкция двух (или любого другого числа) переменных х0 и х1 принимает значение 1 только на наборе, в котором все переменные имеют значения 1. На остальных наборах эта функция имеет значение 0.

Табл. 4.5.2 Функция И

Таблица 4.5.2 представляет собой таблицу истинности конъюнкции двух переменных х0 и x1. ЛФ конъюнкция обозначается в виде x 0 x1 . Для обозначения конъюнкции можно

использовать символы или &. Конъюнкция называется также «операцией И». Функция И выполняется электронной схемой, которая называется «элементом И» или конъюнктором. Обозначение элемента И на функциональных схемах показано на рис. 4.5.2 Число входов элемента И равно числу переменных, участвующих в операции умножения.

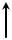x 0

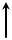x1

f

Рис.4.5.2. Обозначение и временная диаграмма коньюнктора

Логическое сложение (дизъюнкция). Дизъюнкция двух (или любого другого числа) переменных х0 и х1 имеет значение 0 только на наборе, в котором все переменные имеют значение 0. Если хотя бы одна из переменных равна 1, функция будет иметь значение 1.

Табл. 4.5.3 Функция ИЛИ

Таблица 4.5.3 есть таблица истинности для дизъюнкции двух переменных х0 и х1. ЛФ дизъюнкция записывается в виде x0 x1 . Кроме символа + для дизъюнкции употребляется символ . Дизъюнкция называется также «операцией ИЛИ».

Операция ИЛИ реализуется электронной схемой, которая называется «элементом ИЛИ» или дизьюнктором. Обозначение элемента ИЛИ на функциональных схемах показано на рис. 4.5.3. Число входов элемента ИЛИ равно числу переменных, участвующих в операции дизъюнкции.

x 0

t

x1

t

f

t

Рис.4.5.3. Обозначение и временная схема дизьюнктора

3.6. Основные законы алгебры логики.

Формулы, представляющие одну и ту же функцию называются эквивалентными или равносильными и обознаются =. Основные законы алгебры логики позволяют проводить эквивалентные преобразования логических функций, приводить их к удобному для дальнейшего использования виду и упрощать запись:

Ассоциативность конъюнкции и дизъюнкции: x0(x1x2)=(x0x1) x2=x0x1x2, x0+(x1+x2)=(x0+x1)+x2=x0+x1+x2.

Коммутативность конъюнкции и дизъюнкции: x0x1=x1x0, x0+x1=x1+x0.

Дистрибутивность:

x0 (x1+x2)=x0x1+ x0x2, x0 + x1x2=( x0 + x1)( x0 + x2).

Идемпотентность (отсутствие степеней): xx=x, x+x=x.

Закон двойного отрицания:

xx .

Свойства констант 0 и 1: x·1=x, x·0=0, x+1=1, x+0=x.

Теорема двойственности (правила де Моргана):

x 0 x 1 x 0 x 1 , x 0 x 1 x 0 x 1 .

Закон противоречия:

xx 0 .

Закон исключения третьего:

x x 1 .

Табл. 4.7.2 Функция ИЛИ-НЕ

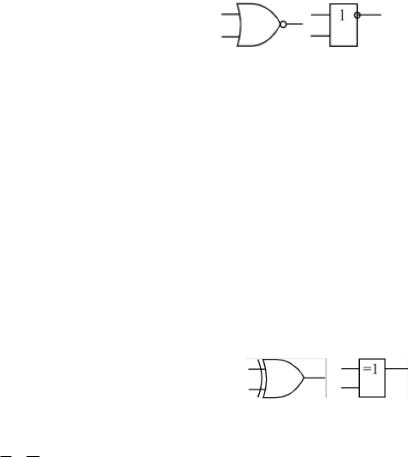
ИЛИ-НЕ выполняет электронный элемент, который называется «элементом ИЛИНЕ». Обозначение элемента ИЛИ-НЕ на функциональных схемах показано на рис. 4.4.2. Число входов элемента ИЛИ-НЕ определяется числом аргументов функции ИЛИ-НЕ.

Рис.4.7.2. Обозначение ИЛИ-НЕ

Исключающее ИЛИ (НЕРАВНОЗНАЧНОСТЬ или сложение по модулю два). Дан-

ная функция имеет значение 1 на тех наборах переменных, в которых число единиц нечетно. Для двух переменных функция НЕРАВНОЗНАЧНОСТЬ иллюстрируется таблицей истинности (табл. 4.7.3). Эта функция записывается для двух переменных в виде x0 x1 .

Табл. 4.7.3 Функция ИСКЛЮЧАЮЩЕЕ ИЛИ

Условное обозначение элемента, выполняющего функцию НЕРАВНОЗНАЧНОСТЬ, на функциональных схемах приведено на рис. 4.7.3

Рис.4.7.3. Обозначение ИСКЛЮЧАЮЩЕГО ИЛИ

Операция НЕРАВНОЗНАЧНОСТЬ выражается через операции НЕ, И, ИЛИ в виде

f x0 x1 x0 x1 .

Исключающее ИЛИ–НЕ (РАВНОЗНАЧНОСТЬ). Функция РАВНОЗНАЧНОСТЬ представляет собой отрицание операции ИСКЛЮЧАЮЩЕЕ ИЛИ.

Данная функция имеет значение 1 на тех наборах переменных, которые содержат четное число единиц. Для двух переменных ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ представлена таблицей истинности (табл. 4.7.4).

Табл. 4.7.4 Функция РАВНОЗНАЧНОСТЬ

обозначение элемента, выполняющего функцию НЕРАВНОЗНАЧНОСТЬ, на функциональных схемах приведено на рис. 4.7.4.

Примером логического выражения, являющегося элементарной дизъюнкцией могут

служить x 0 + x 1 + x 2 , x 0 + x 1 , x 0 x 1 + x 2 , а выражения вида x 0 + x 1 + x 2 , x 0 + x 1 , не являются элементарными дизъюнкциями.

Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций.

Совершенной КНФ (СКНФ) называется КНФ, каждая элементарная дизъюнкция которой включает все переменные с отрицанием или без.

СКНФ также может быть получена из таблицы истинности: для каждого набора аргументов на котором функция равна «0» составляют элементарную сумму, причем переменные, значение которых равно «1», записываются с отрицанием. Полученные суммы, которые носят название конституент нуля, или макстермов, объединяют операцией логического умножения. Например, СКНФ для функции из предыдущего примера имеет

Иногда удобнее пользоваться не самой логической функцией, а ее инверсией. В этом случае при использовании вышеописанных методик для записи СДНФ надо использовать нулевые, а для записи СКНФ – единичные значения функции. Конъюнктивные формы представления ЛФ используются реже, чем дизъюнктивные.

3.9. Минимизация логических функций.

Под минимизацией логической функции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.

Минимизация ЛФ необходима, чтобы обеспечить минимум затрат оборудования при построении функциональной схемы в заданном базисе логических элементов. Чаще всего используется набор {И, ИЛИ, НЕ}, а минимизация ЛФ ведется в ДНФ. В рамках нормальных форм минимальной будет такая разновидность функции, которая состоит из наименьшего количества дизъюнктивных членов при наименьшем суммарном числе символов переменных.

Вопрос минимизации логических функций решается на основе применения законов склеивания и поглощения с последующим перебором получаемых дизъюнктивных форм и выбором из них минимальной. Существует большое количество методов минимизации логических функций. Среди методов минимизации можно выделить аналитические методы и табличные. Табличные методы минимизации отличаются большей наглядностью и меньшей трудоемкостью, однако их применение эффективно при малом числе переменных. Аналитические методы минимизации формул булевых функций основаны на использовании соотношений булевой алгебры.

Пример 1: Упростить булеву формулу:

f x 0 , x 1 , x 2 x 0 + x 0 x 2 + x 0 x 1 x 2 + x 1 x 2 x 0 + x 0 x 1 x 2 + x 1 x 2 x 0 + x 1 x 2 + x 1 x 2 = x 0 + x 1 (x 2 + x 2 )= x 0 + x 1 .

Пример 2: Упростить булеву формулу: f x 2 x 3 ( x0 x0 x1 )( x0 x 0 x1 ) x1 x0

Применяя к данной функции законы и тождества алгебры логики, осуществляем ее минимизацию:

f x 2 x3 ( x 0 x 0 x1 )( x 0 x 0 x1 ) x1 x 0 x 2 x3 x 0 (1 x1 )( x 0 x1 ) x1 x 0

x 2 x3 x 0 ( x 0 x1 ) x1 x 0 x 2 x 3 x 0 (1 x1 x1 ) x 2 x 3 x 0 .

Один из популярных алгоритмов минимизации был изобретен в 1952 Эдвардом В. Вейчем и усовершенствован в 1953 Морисом Карно, физиком из «Bell Labs». Этот алгоритм минимизации использует карты Карно и выглядит следующим образом:

1.Смежные единицы карты Карно функции n переменных условно охватывают

(накрывают) прямоугольными контурами. Каждый контур может содержать

1,2,4, ... 2n единиц.

2.Одним контуром необходимо объединить максимальное количество смежных клеток, содержащих единицы.

3.Необходимо, чтобы каждая единица накрывалась хотя бы один раз.

4.Одна и та же единица может охватываться несколько раз разными контурами.

5.Крайние клетки каждой горизонтали и каждой вертикали граничат между собой (топологически карта Карно для четырех переменных представляет собой тор- «бублик»). Следствием этого правила является смежность всех четырех угловых ячеек карты Карно для n=4.

6.Результатом минимизации является булево выражение в ДНФ. Количество конъюнкций в ДНФ соответствует числу контуров.

7.В результирующие конъюнкции входят переменные, не меняющие свои значения в клетках, причем в прямой форме, если соответствующие им строки и столбцы диаграммы помечены единицей. Переменные, связанные со строками и столбцами, помеченными нулем, входят в конъюнкции в инверсной форме.

f М Д Н Ф = x 0 x 1 x 0 x 2 x 1 x 2 .

Справедливости ради надо отметить, что сформулированная задача минимизации ЛФ являлась чрезвычайно актуальной в тот период времени, когда разработка цифровых устройств велась на электромеханических переключательных элементах, дискретных радиокомпонентах и интегральных схемах малой степени интеграции.

Достигнутые в настоящее время схемотехнологические успехи в микроэлектронике, в частности создание схем средней, большой и сверхбольшой интеграции позволяют реализовать очень сложные системы ЛФ практически, используя один корпус без какихлибо процедур минимизации.

3.10. Функционально полные системы логических функций.

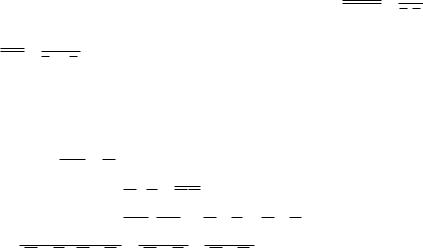
Набор элементарных логических функций называется функционально полным (базисным), если с его помощью можно записать в виде формулы любую логическую функцию. Легко доказать, что набор функций {И, ИЛИ, НЕ} является функционально полным.

Свойствами функциональной полноты обладают также наборы {И, НЕ} и {ИЛИ, НЕ}. Действительно, в наборе {И, НЕ} функцию ИЛИ можно выполнить через операции

И, НЕ путем эквивалентного преобразования f x0 x1 x0 x1 x0 x1 . В наборе {ИЛИ, НЕ} функцию И можно выполнить через операции ИЛИ и НЕ следующим образом:

f x0 x1 x0 x1 x0 x1 . Таким образом, набор функций {И, ИЛИ, НЕ} обладает избыточностью.

Штрих Шеффера или стрелка Пирса также образуют базис пространства булевых функций от двух переменных. То есть, используя например, только штрих Шеффера можно построить остальные операции:

x 0 | x 0 x 0 x 0 x 0 о т р и ц а н и е

( x 0 | x 0 ) | ( x1 | x1 ) x 0 | x1 x 0 x1 x 0 x1 д и з ъ ю н к ц и я

( x 0 | x1 ) | ( x 0 | x1 ) x 0 x1 | x 0 x1 ( x 0 x1 ) | ( x 0 x1 )

( x 0 x1 )( x 0 x1 ) ( x 0 x1 ) ( x 0 x1 ) x 0 x1 x 0 x1 x 0 x1 к о н ъ ю н к ц и я .

Это позволяет реализовать всю необходимую логику с использованием единственного типового элемента. С другой стороны, использование других типовых элементов позволит уменьшить их общее количество и тем самым повысить надежность схемы. На практике, с целью уменьшения номенклатуры используемых микросхем, часто пользуются функционально полной системой логических элементов в составе двух, выполняющих операций И-НЕ, ИЛИ-НЕ.

При преобразовании к базису И-НЕ логическая функция, минимизированная в основном базисе, представляется в форме МДНФ и затем путем двойного инвертирования исходного выражения или его части и применения теорем де Моргана приводится к виду, содержащему только операции логического умножения и инвертирования, т.е. базису И- НЕ.

При преобразовании к базису ИЛИ-НЕ, исходную логическую функцию приводят к МКНФ, содержащей только операции логического сложения и инверсии. Далее логическое выражение записывается через условные обозначения ИЛИ-НЕ.

Пример: Привести в базис И-НЕ и ИЛИ-НЕ мажоритарную функцию трех переменных. а) приводим функцию к базису И-НЕ:

б) приводим функцию к базису ИЛИ-НЕ: