§ 2. Числовые множества, их границы

Действительные числа изображаются, как известно, точками числовой прямой, причем каждому действительному числу соответствует одна точка числовой прямой и обратно, каждой точке числовой прямой соответствует только одно действительное число. Как говорят, установлено взаимно-однозначное соответствие между множеством точек числовой прямой и множеством действительных чисел. Поэтому, говоря о числовых множествах, мы будем иметь в виду как подмножества множества R действительных чисел, так и подмножества точек числовой прямой.

Определение 1. МножествоЕ действительных чисел называетсяограниченным сверху (соответственно,ограниченным снизу), если существует числоМ, такое, что для любогоимеет место неравенство(соответственно,). ЧислоМ называетсяверхней (соответственно,нижней)границей (или гранью) множестваЕ. МножествоЕ называетсяограниченным, если существуют такие числаи, что для любого числаимеет место двойное неравенство.

Например, множество правильных дробей ограничено сверху числом 1, множество N натуральных чисел ограничено снизу числом 1, множествоограничено, так как.

Заметим, что если М– верхняя граница непустого ограниченного сверху числового множестваЕ, то любое число, большееМ, также будет его верхней границей, то есть уЕ есть бесконечное множество верхних границ. Из всех верхних границ множестваЕ наибольший интерес представляет его наименьшая верхняя граница.

Определение 2. Наименьшая из верхних границ множестваЕ называется еготочной верхней границей (или точной верхней гранью) и обозначаетсяsup E (от латинского словаsupremum– наивысшее).

Аналогично вводится понятие точной нижней границы множества Е, ограниченного снизу.

Определение 3. Наибольшая из нижних границ множестваЕ называется еготочной нижней границей (или точной нижней гранью) и обозначаетсяinf E (от латинского словаinfimum– наинизшее).

Имеет место

Теорема 1. Всякое непустое и ограниченное сверху (соответственно, снизу) числовое множествоЕ имеет точную верхнюю (соответственно, нижнюю) границу.

Доказательство. Проведем его для случая верхней границы. Рассмотрим два случая.

1) Предположим сначала, что среди чисел х множестваЕ найдется наибольшее. Тогда все числа множества будут удовлетворять неравенству, т.е.– верхняя граница множестваЕ. С другой стороны, поскольку, то для любой верхней границыМ выполняется неравенство. Отсюда следует, что– точная верхняя граница множестваЕ.

2) Пусть теперь среди чисел х множестваЕ нет наибольшего. Произведем сечение множестваR действительных чисел следующим образом. К верхнему классуотнесем все верхние границымножестваЕ, а к нижнему классуА все остальные действительные числа. При этом все числапопадут в классА, так как среди них нет наибольшего. По теореме Дедекинда существует действительное число, производящее данной сечение. Все числа, как принадлежащие классуА, не превосходят этого пограничного числа, т.е.– верхняя граница множестваЕ, т.е.и является внаименьшим числом по теореме Дедекинда. Поэтому.

Аналогично доказывается вторая часть теоремы о существовании точной нижней границы (это могут сделать студенты дома самостоятельно). Теорема доказана.

Из школьного курса математики известны некоторые специальные числовые множества: –интервал(открытый промежуток),–отрезок(замкнутый промежуток),,–полуинтервалы(открытый справа и слева соответственно),– вся числовая прямая,– лучи. Отрезки, интервалы и полуинтервалы называютсяпромежутками.

Определение 4. Еслиа– некоторое действительное число,– любое положительное действительное число, то интервалназывается-окрестностьюточкиа. Точкааназываетсяцентромокрестности, а число-радиусомокрестности. Множество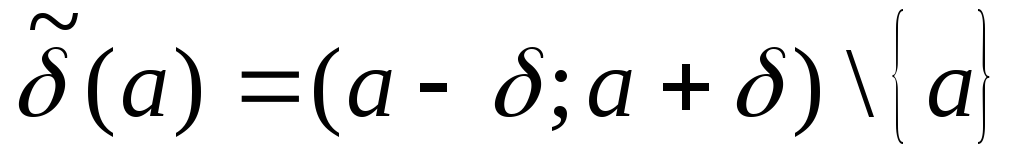называетсяпроколотой- окрестностью точкиа.