Решение задачи Коши методом конечных разностей.

Здесь различают две группы методов:

а) Одношаговые: в них для нахождения решения в некоторой точке используется информация лишь в одной предыдущей точке (или предыдущем шаге). К этим методам относятся: метод Эйлера, метод Рунге – Кутта;

б) Многошаговые: для отыскания решения в некоторой точке(шаге) используют информацию о решении в предыдущих точках(шагах). К ним относится метод Адамса.

Рассмотрим применение этих методов к дифференциальным уравнениям первого порядка. Так как дифференциальные уравнения «n» - го порядка можно свести к системе уравнений первого порядка, а алгоритм решения системы дифференциального уравнения можно легко получить из алгоритма для решения одного уравнения.

Отметим, что указанные методы применимы для хорошо обусловленных задач, то есть таких решений, которые мало изменятся при изменении начальных условий.

Численные методы решения обыкновенных дифференциальных уравнений

Обыкновенным дифференциальным уравнением называется уравнение вида

F(x, y, )=0

где x – независимая переменная, y – искомая функция, – производные вплоть до n – го порядка. n – порядок дифференциального уравнения.

В качестве независимой переменной вместо x может быть t. Общим решением ОДУ называется функция

y(x) = y(x, )

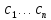- n постоянных интегрирования.

Чтобы получить частное решение, удовлетворяющее данной конкретной задаче, необходимо определить дополнительные условия. Число этих условий равно порядку дифференциального уравнения.

В зависимости от способа задания дополнительных условий для получения частного решения дифференциального уравнения существуют два различных типа задач:

а) Задача Коши; б) Краевая задача.

Если эти условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями, а точка x = 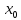, или t=0 (решение отыскивается при t ≥ 0), в которой они задаются – начальной точкой.

Задача называется краевой, если дополнительные условия задаются более чем в одной точке, то есть при разных значениях независимой переменной. Сами дополнительные условия называются при этом граничными или краевыми условиями. На практике обычно граничные условия задаются в двух точках x = a, x = b, являющихся границами области.

Численное решение краевой задачи для оду.

Пусть имеем систему ОДУ:

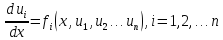
и дополнительные условия, налагаемые на 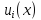не менее чем в двух точках отрезка (могут и на краях и во внутренних точках). Следовательно, краевая задача ставится для системы дифференциального уравнения не ниже второго порядка (или одного дифференциального уравнения порядка не ниже второго).

В краевые условия могут входить значения нескольких функций, производных, или и функций и производных.

Метод стрельбы

Пусть имеем дифференциальное уравнение второго порядка:

и краевые условия u(a) = α, u(b) = β.

Основная идея метода стрельбы в сведении краевой задачи к решению серии задач Коши.

Чтобы поставить задачу Коши необходимо в какой – либо одной точке поставить два условия (так как второй порядок дифференциального уравнения)

В точке «a» есть условие: u(a) = α. 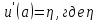- произвольное. Итак мы имеем задачу Коши

u(a) = α

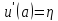
Решая эту задачу Коши каким – либо известным методом будем получать решение, зависящее от η. Нам надо менять η так, чтобы выполнялось

F(η) = U(η, b) – β = 0, то есть находится корень этого уравнения.

То есть решается серия задач Коши и находятся табличные значения F(η). Решают задачу Коши до тех пор пока не найдутся средние F(η), различающиеся по знаку, значит между соответствующими им есть η, в которой F(η) = 0. Можно это η найти методом ______ или, например, методом секущей.

Решение краевой задачи с обыкновенным дифференциальным уравнением методом конечных разностей.(общая методология)

Пусть имеем дифференциальное уравнение второго порядка, разрешенное относительно второй производной: a ≤ x ≤ b

(x, u, 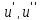)=0 с граничными условиями U(a)=A; U(b) = B.

Граничные условия могут быть также заданы и в виде:

то есть в них участвуют и производные.

Заменим производные, входящие в эти соотношения конечно – разностными аппроксимациями

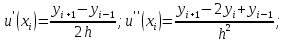
Подставляя эти выражения в исходное дифференциальное уравнение, получим систему разностных уравнений

F(x, )=0 i=1,2,…n-1, i - номер узлов.

Отрезок 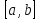разбит на «n» равных частей; . Если u(a) =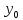; u(b) =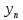, то граничные условия в разностном виде.

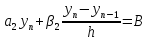
из этих соотношений можно найти .

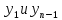Таким образом решение краевой задачи сводится к решению системы алгебраических уравнений (линейных или нелинейных – зависит от вида f). Методы их решения мы уже рассматривали.

Например, для дифференциальных уравнений вида

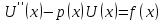
получается система линейных уравнений трех - диагонального вида и она может быть решена методом прогонки.

Конечно – разностный метод решения краевой задачи для обыкновенных дифференциальных уравнений.

Основная идея: сведение краевой задачи сразу к решению системы алгебраических уравнений путем замены производных в дифференциальном уравнении и краевых условий конечно – разностными аппроксимациями.

Пример

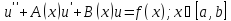
u(a) = α, u(b) = β.

Вводим на 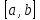сетку a = с постоянным шагом h.

Воспользуемся для аппроксимации производных формулами численного дифференцирования.

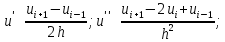
где i = 1,2,…,n-1

Подставим, получим:

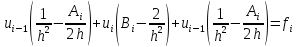
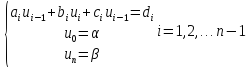
Получаем систему трех – диагональных уравнений, которые можно решать методом прогонки.

Устойчивость и корректность прогонки обеспечивается, как известно условием преобладания диагональных элементов.