
Понятие сходимости
Пусть имеем
дифференциальное уравнение
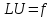 (1)
(1)
Ввели сетку
аппроксимации производные и дополнительные
условия и получили разностную схему
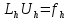 (2)
(2)
Из-за погрешностей
аппроксимации и вычислении ошибок
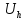 не будет совпадать с истинным решением,
не будет совпадать с истинным решением,
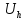 - сеточная функция. Нам важно, чтобы
- сеточная функция. Нам важно, чтобы
 сходилось к
сходилось к
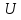 в
узлах. Численное решение сеточной
функции
в
узлах. Численное решение сеточной
функции
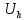 сходится к истинному значению, если
сходится к истинному значению, если
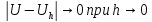 .
.
В теории разностных схем доказывается, что если разностная схема аппроксимирует исходную дифференциальную задачу (то есть дифференциальное уравнение и дополнительные условия) и устойчива, то будет сходимость.
Устойчивость означает, что при малом изменении входных данных (коэффициент уравнения, правых частей, начальных и граничных данных) решение изменяется тоже немного.
Математика это
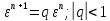
Условие аппроксимации:
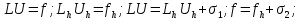
то есть
 эквивалентно.
эквивалентно.
То есть
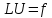 эквивалентно
эквивалентно
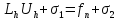 ,
разностная схема аппроксимирует
исходящую дифференциальную задачу,
если при
,
разностная схема аппроксимирует
исходящую дифференциальную задачу,
если при
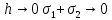
Методы решения краевых задач
-
Аналитические методы.______ в квадратурах, строгое интегрирующее. Простые случаи.
-
Приближенные методы
Упрощения:
а) отбрасываются некоторые члены;
б) выбираются специальные классы ____ уравнений.
2а) метод возмущений
Решение основное + малая доставка (возмущение)
2б) метод малого параметра
Решение = ряд по малому параметру, содержащемуся в задаче
2в) методы минимизации невязок
Суть
метода: Берется система линейных
независимых, дифференциальных функций:
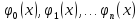 ;
;
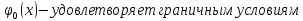 ;
;
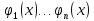 – нулевым граничным условиям. Строится
решение
– нулевым граничным условиям. Строится
решение
y
=
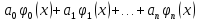
Подставляем в
исходное дифференциальное уравнение
и находится невязка
– разность
между левой и правой частью – r(x,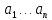 ).
).
Дальше делают так, чтобы r -> к минимуму.
Способ минимизации определяет метод
а) метод
коллокации.
Выбираются точки
 ,
в которых r
= 0. Получается система
линейных уравнений
для
,
в которых r
= 0. Получается система
линейных уравнений
для
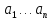 ;
;
б) метод
наименьших квадратов.
Минимизируется сумма квадратов невязок.
Опять система
линейных уравнений
для
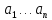 ;
;
в) метод
Бубнова – Галеркина.
Использование требования ортогональности
базисных функций
 к невязке r(x,
к невязке r(x,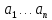 )
)
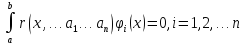
Опять система линейных уравнений
Основные понятия.
Многие задачи физики, механика, химии и других отраслей науки и техники при их математической моде сводятся к дифференциальным уравнениям.
Дифференциальные уравнения делятся на две существенно различные категории:
-
–я : обыкновенные дифференциальные уравнения, которые содержат только одну независимую переменную;
-
-я : уравнения с частными производными, содержащие несколько независимых переменных.
Полная математическая постановка задачи наряду с дифференциальными уравнениями требует _____ дополнительных условий, так называемых краевых условий.
Если решение ищется в ограниченной области значения независимых переменных, то задаются условия на границах области, которые называются граничными (краевыми). Если одной из независимых переменных является время, то задаются некоторые условия в начальный момент времени – это начальные условия.
Если задаются и граничные и начальные условия, то такие задачи называются нестационарными ( или смешанными) краевыми задачами.
Основные методы решения
Аналитические методы – дают возможность провести непосредственное интегрирование дифференциальных уравнений, то есть решение в квадратурах – в виде формул и путем аналитических преобразований – однако, это возможно только в простых случаях.
___________________ методы
Они используют различные упрощения самих дифференциальных уравнения, например, путем отбрасывания содержащихся в них членов, или выбором некоторых специальных классов искомых функций.
К ним относятся:
Метод возмущений. Решение ищется в виде основного решения + малой добавки (возмущения);
Метод малого параметра: решение ищется в виде ряда по некоторому малому параметру, содержащемуся в данной задаче.
Методы минимизации
невязок.
Суть их заключается в следующем. Пусть
задано дифференциальное уравнение с
некоторыми граничными условиями.
Выбирается некоторая линейно независимая
(базисная) система дифференциальных
функций
 (запись для обыкновенных дифференциальных
уравнений)
(запись для обыкновенных дифференциальных
уравнений)
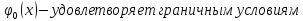 ;
;
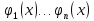 – нулевым граничным условиям.
– нулевым граничным условиям.
Искомое решение представляется в виде линейной комбинации базисных функций
-
y(x) =
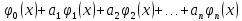
Подставляя это
выражение в исходное дифференциальное
уравнение, можно найти разность между
его левой и правой частями, которая
называется невязкой:
r(x,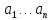 ).
). – подбирается так, чтобы невязка была
минимальна. Способ минимизации и
определяет ту или иную модификацию
метода.
– подбирается так, чтобы невязка была
минимальна. Способ минимизации и
определяет ту или иную модификацию
метода.
а) метод
коллокаций:
выбираются точки
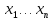 ,
в которых невязки полагаются = 0. Получается
система линейных алгебраических
уравнений, из которых определяется
,
в которых невязки полагаются = 0. Получается
система линейных алгебраических
уравнений, из которых определяется
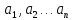 и подставляется в решение (1);
и подставляется в решение (1);
б) метод
наименьших квадратов.
Минимизируется сумма квадратов невязок
– также определяется система линейных
алгебраических уравнений, из которых
находятся
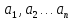 .
.
в) метод конечных разностей(применяется как для общих дифференциальных уравнения, так и для дифференциальных уравнений в частных производных)
Состоит из следующих этапов
-
Построение дискретного аналога непрерывной среды (_______ разностной сетки. Переход к дискретным значениям аргументов и искомой функции). Значения функции в узлах сетки, называются сеточными функциями;
-
Аппроксимация системы дифференциальных уравнений. Производные заменяются разностными аналогами и записываются во внутренних узлах;
-
Аппроксимация начальных или граничных условий. Разностные операторы записываются в граничных узлах. В итоге получается система алгебраических уравнений, число которых пропорционально числу внутренних узлов;
-
Решение получающейся системы алгебраических уравнений и получение дискретных значений искомой функции. Эта система алгебраических уравнений бывает очень высокого порядка, но матрица коэффициентов бывает сильно разреженной;
-
Построение приближающей функции по полученным дискретным значениям искомой функции.
