– Неявная схема
Преимущества, в большинстве случаев устойчивость при любом шаге на времени.
Недостаток
- необходимость на каждом шаге решать,
в общем случае, нелинейное и даже
трансцендентное уравнение. Пример:
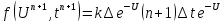
то
есть
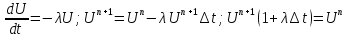
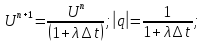при любом
метод устойчив, то есть неявная схема
устойчива.
Итак, явная схема
в случае уравнения
.
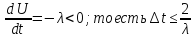А неявная схема в этом же случае устойчива
при любом
.
Особый случай,
когда уравнение имеет нарастающее
решение, то есть вида:
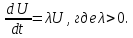
Строгое решение
;
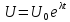тогда явная схема:
,
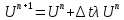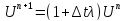при любом
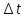неустойчива
,
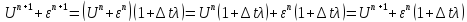
то есть явная схема при любом
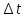неустойчива
Рассмотрим неявную
схему:
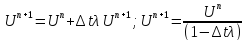
, чтобы
должно быть
,
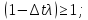
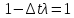то есть
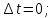то есть и неявная схема при
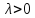так же будет неустойчива. Поттер: «В
некоторых физических задачах возникают
решения, растущие во времени по
.
Тогда можно допустить неограниченное
нарастание ошибки при условии, что они
меньше, чем растущее решение. Пусть
,
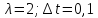тогда:
для
явного метода
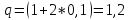
для
неявного метода
Постоянная величина
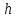и порядка точности
.
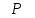Известно о точности
.
Точность
метода Эйлера
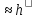первого порядка.
при одинаковых шагах.
Во
сколько раз
нужно уменьшить шаг в методе Эйлера,
чтобы получить погрешность
:
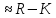Здесь важно насколько мал шаг по сравнению
с 1.
Если
Если
.
То есть в этом случае шаг, в методе
Эйлера надо уменьшить в 1000 раз, в методе
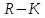нужно четыре раза вычислять значение
функции. Таким образом, в методе Эйлера
в 250раз нужно проводить больше вычислений.
Стадии
Эйлера: а)
- неявный метод
б)
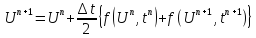- это тоже неявный метод
По-видимому, второй
вариант точнее, так как берется среднее
значение на шаге
,
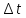а в первом варианте значение на правом
конце
.
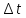в)
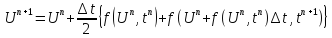
г)
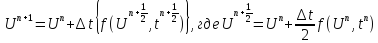
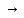это уже
Заранее определяется
формула
.
Наиболее употребительна формула
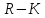четвертого порядка точности, то есть
.
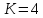Существуют различные модификации
функции четвертого порядка. В частности
,
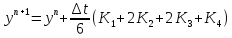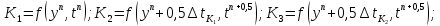
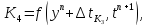где
где
.
В этой схеме нужно
на каждом шаге четвертого ряда вычислять
функцию
.
Может создаться впечатление, что можно
взять схему Эйлера, в ней уменьшить шаг
в 4 раза и таким образом, получить такой
же результат с тем же объемом вычислений.
Однако это не так, особенно при малых
.
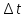есть
неявные модификации.
Применение для схем уравнений на примере системы из двух уравнений.
Пусть
имеем:
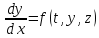
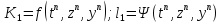
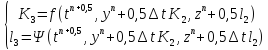
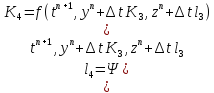
Можно
легко менять шаг
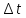
Метод Рунге-Кутты требует большего объема вычислений, чем метод Эйлера, однако это окупается большей точностью, что дает возможность проводить счет с большим шагом. Для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе Рунге-Кутты.
Метод Рунге-Кутты является наиболее употребительным методом.
Многошаговые методы решения задачи Коши для обыкновенных дифференциальных уравнений.
Суть его в том, что
для вычисления значения
используются результаты не одного, а
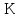предыдущих шагов
.
Разностная схема для задачи Коши:
,
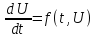с начальным условием
в это случае запишется так:
,
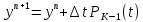где
- интерполяционный многочлен степени
,
который аппроксимирует функцию
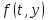на отрезке
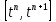по значениям функции
.
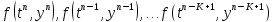Широко распространенным является метод
Адамса. Простейший из них при
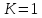совпадает с методом Эйлера. В практических
расчетах чаще всего используется вариант
метода Адамса, имеющий четвертый порядок
точности и использующий результаты
предыдущих четырех.
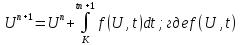- на
участке
аппроксимирована на __________
_______________________________предыдущих
четырех узлах. При этом так же вычислены
ранее значения правой части:
.
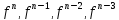В качестве интерполяционного многочлена
используется многочлен Ньютона. В случае
постоянного шага
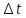разностная схема четвертого порядка
метода Адамса:
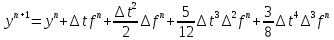
где
По сути, используется формула Симпсона.
Преимущества:
экономичен, так как требует вычисления
лишь одного значения правой части на
каждом шаге (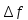
–
пересчитывается).
Недостатки:
расчет по этому методу можно начать
лишь с
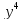- то есть с четвертого значения в четвертом
узле.
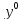- задается как начальное условие.
Необходимые при этом
можно определить методом Рунге-Кутты,
что усложняет общий алгоритм. Кроме
того без усложнения формул в методе
Адамса нельзя менять шаг
.
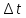В одношаговых методах менять шаг просто.
Метод прогноза и коррекции на основе
методов Адамса.
О повышении точности численного решения.
Одним из путей
является уменьшение шага, но при этом
может снизить существенно объем
вычислений. На практике для повышения
точности без повышения машинного времени
используется метод Рунге. Он состоит в
том, что проводятся повторные расчеты
по одной разностной схеме с различными
шагами. Предположим, были расчеты шагами
,
тогда в соответствии с методом Рунге
значение
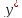в узлах сетки с шагом вычисляется по
формуле:
_______
порядок точности решения
,
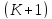хотя используется разностная схема
имеет порядок точности
.