
Решение задачи Коши для обыкновенного дифференциального уравнения мкр
Требуется найти
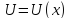 ,
удовлетворяющую уравнению:
,
удовлетворяющую уравнению:
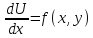
При этом должно быть:
Начальные условия:
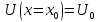 решение
решение
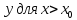
Введем сетку:
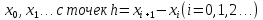 .
В каждой точке
.
В каждой точке
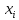 вместо значений функции
вместо значений функции
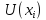 вводятся
вводятся
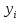 ,
аппроксимирующие точки решения на
заданном множестве точек. То есть
,
аппроксимирующие точки решения на
заданном множестве точек. То есть
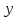 – сеточная функция.
– сеточная функция.
Далее заменяя
производную конечными разностями
осуществляем переход от дифференциальной
задачи к дискретной (разностной)
относительно сеточной функции
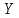 :
:
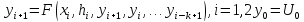
Конкретное выражение в правой части зависит от способа аппроксимации производной. Для каждого численного метода получается свой вид уравнения. На этой основе можно провести классификацию численных методов задачи Коши для обыкновенных дифференциальных уравнений.
Если в правой части
отсутствует
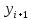 ,
то есть
,
то есть
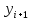 явно вычисляется по
явно вычисляется по
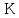 предыдущим значениям
предыдущим значениям
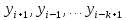 ,
тогда разностная схема называется
явной.
Поскольку используется несколько
предыдущих значений
,
тогда разностная схема называется
явной.
Поскольку используется несколько
предыдущих значений
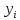 ,
то схема называется многошаговой.
,
то схема называется многошаговой.
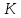 – число шагов. При
– число шагов. При
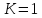 в
правой части только
в
правой части только
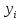 - то есть метод одношаговый.
- то есть метод одношаговый.
Если в правой части
присутствует
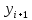 ,
то решение усложняется. Приходится
решать уравнение относительно
,
то решение усложняется. Приходится
решать уравнение относительно
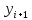 ,
чтобы в правой
,
чтобы в правой
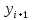 .
Такие методы называются неявными.
.
Такие методы называются неявными.
Одношаговые
методы.
Простейший – метод Эйлера. Обычно при
решении физических задач, связанных с
задачей Коши, в качестве независимой
переменной является время
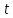 .
Поэтому вместо
.
Поэтому вместо
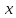 у нас будет
у нас будет
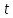 ,
что, конечно, на суть излагаемых методов
никак не влияет.
,
что, конечно, на суть излагаемых методов
никак не влияет.

Задано начальное
условие
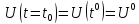
Обычно индексы,
относящиеся ко времени
 пишутся сверху, а к пространственным
координатам снизу.
пишутся сверху, а к пространственным
координатам снизу.
Вводим сетку с
узлами
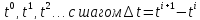
Далее заменяем
производную через конечные разности и
переходим к сеточной функции
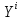 ,то есть
,то есть
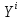 обозначает приближенное значение
обозначает приближенное значение
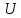 в данном
в данном
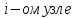 .
.
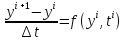
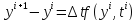 ;
;
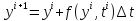
Начальное условие:
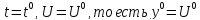 полагая
полагая
 ,
находим:
,
находим:
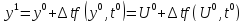
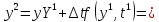
…
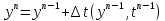
Оценим порядок точности аппроксимации метода Эйлера и его устойчивость
Итак, имеем
дифференциальное уравнение
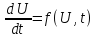
и схему Эйлера
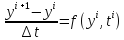
Пусть
 - точное значение искомой функции в узле
- точное значение искомой функции в узле
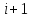 . Изложим его в ряд Тейлора:
. Изложим его в ряд Тейлора:
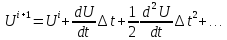
по
времени:

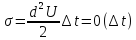
Пусть на
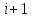 шаге
шаге
 ,
а на
,
а на
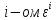 ,
,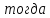 ,
воспользовавшись схемой Эйлера, мы
можем записать
,
воспользовавшись схемой Эйлера, мы
можем записать
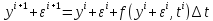
Пусть
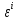 мало
мало
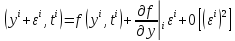
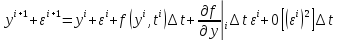
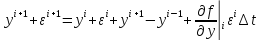
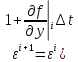
Чтобы метод был устойчив ____________
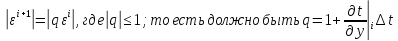
 для
этого необходимо, чтобы
для
этого необходимо, чтобы
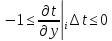 то есть должно быть
то есть должно быть
 ;
;
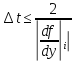
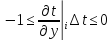 – это функция особенность явных схем,
шаг имеет определенные ограничения.
– это функция особенность явных схем,
шаг имеет определенные ограничения.
Пример:
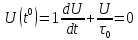 уравнение описывает затухание, лежа
цепи с
уравнение описывает затухание, лежа
цепи с
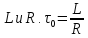
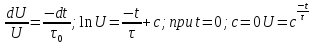
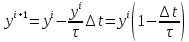
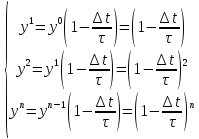
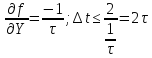
Дадим ещё одну схему Эйлера: схема Эйлера с пересчетом.
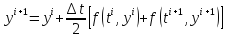
то
есть правую часть мы представляем не
как
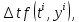 а как среднее арифметическое между
а как среднее арифметическое между
 и
и
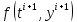 .
.
Полученная
разностная схема является неявной, так
как искомое значение
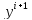 входит в обе части соотношения (равенства)
правую и левую.
входит в обе части соотношения (равенства)
правую и левую.
Анализ показывает,
что вне зависимости от шага
 схема является устойчивой. Это огромное
преимущество. Недостаток, что
схема является устойчивой. Это огромное
преимущество. Недостаток, что
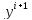 входит неявно и решение относительно
входит неявно и решение относительно
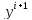 может привести к достаточно сложному
полному алгебраическому
уравнению.
может привести к достаточно сложному
полному алгебраическому
уравнению.
Метод Рунге-Кутта
Для вычисления
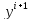 можно применить один из итерационных
методов: например ____. Считая
можно применить один из итерационных
методов: например ____. Считая
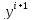 начальным приближением вычисления
начальным приближением вычисления
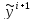 по явной схеме Эйлера:
по явной схеме Эйлера:
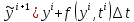 .
Это значение подставляем в схему с
пересчетом:
.
Это значение подставляем в схему с
пересчетом:
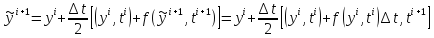 .
Метод Эйлера с пересчетом имеет второй
порядок точности – это модификация
метода Рунге-Кутта второго порядка.
.
Метод Эйлера с пересчетом имеет второй
порядок точности – это модификация
метода Рунге-Кутта второго порядка.

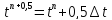
Схема Эйлера с
пересчетом дает второй порядок точности
уже после первой итерации.
Дальнейшие итерации дают более точное
решение уравнения, но не повышают порядок
точности нахождения
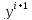 .
Метод Рунге-Кутта четвертого порядка
можно привести без вывода.
.
Метод Рунге-Кутта четвертого порядка
можно привести без вывода.
Неявные методы имеют менее жесткие ограничения на шаг, поэтому, несмотря на то, что решения нелинейного уравнения общее число операций может быть даже менее им в явных методах.
Метод Эйлера-Коши имеет третью ___погрешности на каждом шаге, а по всем интервалам числа интегрирования погрешности пропорциональной навстречу шага, поэтому метод является второго порядка.
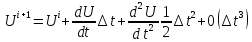
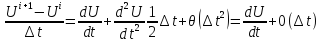

Итого: Для нарастающих
решений явный метод – неустойчив при
любых
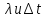 .
Неявный метод – для некоторых соотношений
.
Неявный метод – для некоторых соотношений
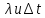 будет иметь
будет иметь
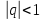 ,
то есть устойчив. При этом при определенных
,
то есть устойчив. При этом при определенных
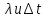 - явный будет, скажем так устойчивее,
чем неявный.
- явный будет, скажем так устойчивее,
чем неявный.
Поттер: численная
устойчивость будет иметь место при
условии
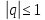
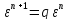
Схема устойчива: если на любой стадии вычисления процесса малая ошибка приводит к меньшей ошибке.
С другой стороны,
если
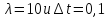
тогда
для явной схемы
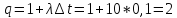
для
неявной схемы
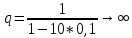
если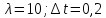
то
для явной схемы
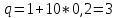
для
неявной схемы
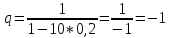 то значит
то значит
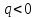
то
есть

