2.5.3.4 Сума гармонійних реалізацій з випадковими фазами нормального гаусового шуму

При визначенні виразу для ДФР сумарного процесу покладемо, що нормальний шум описується щільністю вірогідності (2.85) при m_x=0, а гармонійна напруга описується щільністю розподілу вірогідності

і що ці два процеси незалежні (некорельовані). Тоді приріст сумісної вірогідності попадання гармонійного коливання в інтервал і шуму в інтервалможна записати в наступному вигляді

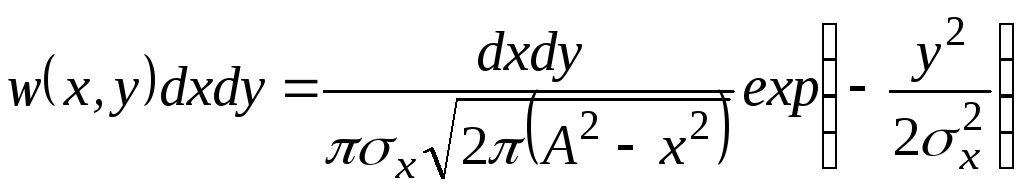. (2.89)

Після заміни змінних у виразі (2.89) і інтегрування його, отримаємо

.

Звідси отримаємо вираз для w(z)

.

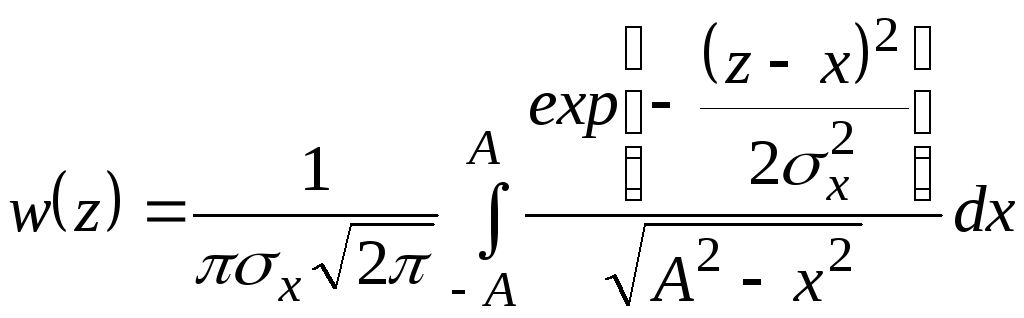Даний вираз є інтеграл згортки ДФР з двох складових випадкових процесів, графічне зображення якого показане на рис.2.28.

Для обчислення інтеграла згортки при деякому значенні будується графік функціїw(х), а також функції , що є графіком функціїw(у), дзеркально перевернений відносно початку координат і зміщений на величину . Потім будується графік добутку ординаті чисельним методом визначається площа під цією функцією. Отримана площа є щільністю вірогідності.

Виконавши аналогічні обчислення для інших значень і з'єднавши знайдені точки плавної кривої, отримуємо результуючу функцію сумісної щільності вірогідності двох випадкових процесів.

Вираз (2.89) остаточно приводиться до вигляду

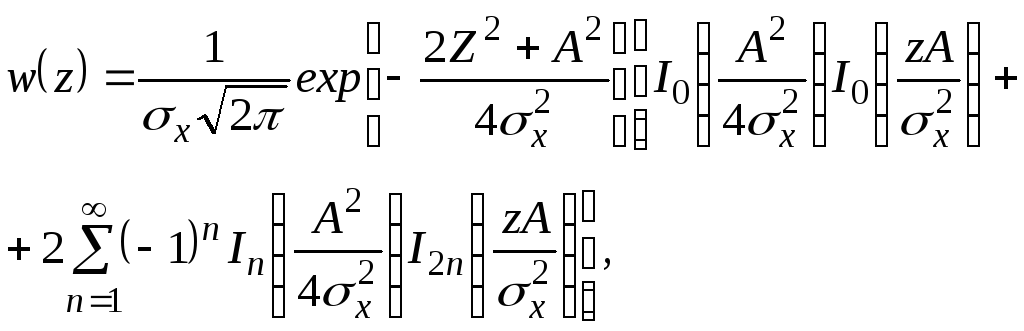
де - модифіковані функції Беселя 1-го роду нульового іn-го порядків. На практиці при розрахунку обмежуються значеннями функції Беселя 1-го порядку (n=1).

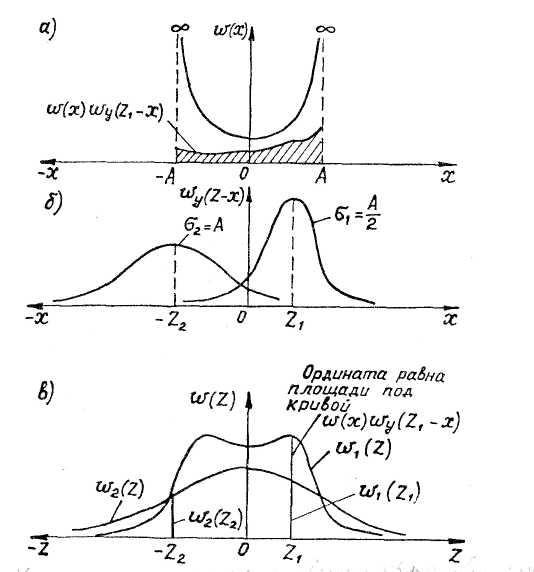
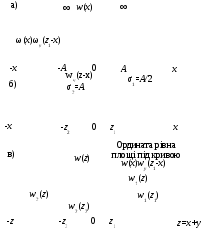
Рисунок 2.28 - До пояснення інтеграла згортки ДФР двох випадкових процесів

На рис.2.29 приведені графіки ДФР або щільності вірогідності розподілу сумарного процесу (гармонійних коливань з випадковою фазою і гаусів шум) для змінної при різних співвідношеннях. Щільність вірогідності розподілу ненормованої змінноїрозраховується по формулі

.

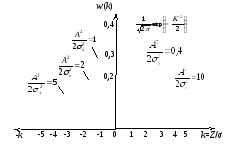
Рисунок 2.29 - Графіки ДФР суми гармонійних коливань з випадковими фазами і гаусова шуму

Аналіз графіків, приведених на рис. показує, що при значеннях відносин щільність вірогідності розподілу амплітуд сумарного процесу підкоряється нормальному закону, тобто функція розподілуw(k) має один максимум при k=0 і переважаючий вплив тут має шумовий процес. При відбувається деформація кривої, тобто перерозподіл щільності вірогідності із збільшенням останньої при відхиленнях змінноїв обидві сторони від її нульового значення. Таким чином, має місце переважаючий вплив на щільність розподілу вірогідності гармонійного процесу з випадковою фазою.

2.5.3.5 Розподілення Пуассона

Часто на практиці доводиться аналізувати процес, який представляє послідовність моментів (точок), розташованих випадковим чином, наприклад, на осі часу. Такі точки можуть відповідати різним подіям, наприклад, моментам часу надходження заявок на обслуговування або моментам часу появи відмов в якій-небудь системі і ін. Точковий випадковий потік використовується в задачі розподілу викликів на телефонній станції протягом доби (рис.2.30).

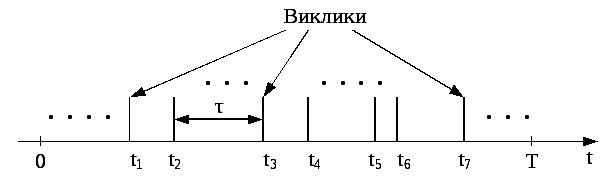
Рисунок 2.30 - Точковий випадковий потік викликів в інтервалі Т

Загальне число викликів протягом доби є випадковим величиною. Для кожного часового інтервалу Т шляхом спостережень можна встановити середнє число викликів (математичне очікування), деλ – інтенсивність (частота) викликів в одиницю часу. Тоді вірогідність появи k-викликів на інтервалі (0,Т) часто визначається формулою Пуассона [18]

. (2.90)

З цього виразу витікає, що вірогідність відсутності на цьому інтервалі викликів буде рівна

.

Вирази для функцій розподілу вірогідності випадкових дискретних величин отримаємо таким чином. Хай деяка випадкова величина Х може приймати одне з m можливих значень , деi - порядковий номер відповідного дискретного значення. Позначимо через вірогідність того, що випадкова величинаХ прийме конкретне значення . Приклад характеру розподілу цієї випадкової величини (ВВ) показаний на рис.2.31. При цьому сума вірогідності всіх можливих значень ВВ завжди рівна одиниці, оскільки сукупність подійутворює повну групу.

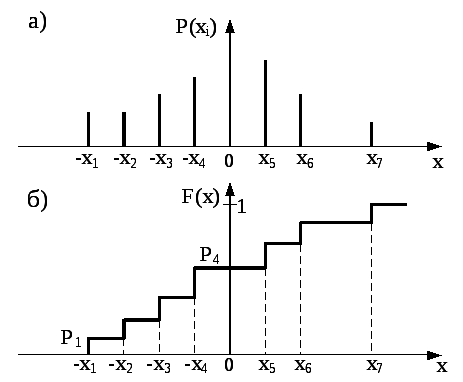
Рисунок 2.31 - Розподіл вірогідності дискретної випадкової величини (а) і її інтегральна функція розподілу (б)

Виберемо на осі абсцис рис.2.31,а деяку довільну точку х, яку розглядатимемо як незалежну змінну. Тоді одномірна ІФР випадкової величини Х може бути записана у вигляді

, (2.91)

де - одинична функція, що починається в точціх_i. Вид F(x) зображений на рис.2.31,б. Оскільки підсумовування в (2.91) проводиться по всіх точках, то ІФР дискретної випадкової величини має ступінчастий характер з скачками в точках можливих значень випадкової величини.

Якщо використовувати δ-функцію, то можна визначити щільність розподілу вірогідності для дискретного розподілу в наступному вигляді

.

Ця функція також має дискретний характер.