Глава 2математичні моделі повідомлень, сигналів і завад

2.1 Функціональні простори і їх базиси

Електричні сигнали складної форми за своєю фізичною природою не завжди подібні звичним для нас уявленням про вектори як про направлені відрізки. Часто на практиці використовують векторне представлення сигналів (функцій). Річ у тому, що серед різних математичних прийомів, застосовуваних при дослідженні електричних кіл і сигналів найширше використовується уявлення довільної функції у вигляді суми більш простих (“елементарних”) функцій, які можна представити векторами.

Такий підхід лежить в основі принципу незалежності дії (суперпозиції) при вивченні перетворень сигналів у лінійних електричних колах. Наочні геометричні представлення, пов'язані з відображенням функції як векторів простору сигналів, допомагають часто усвідомити фізичну сутність процесів формування, передачі і поділу сигналів у лінійних електричних колах. Наочні геометричні представлення, пов'язані з відображенням функцій як векторів простору сигналів, допомагають часто усвідомити фізичну сутність процесів формування, передачі і поділу сигналів, синтезу оптимальних сигналів і пристроїв обробки сигналів при наявності завад.

Розкладання сигналу складної форми на найпростіші складові подібне до розкладання звичайного вектора x тривимірного простору на його складові по координатному базису одиничних ортогональних векторів i, j, k (рис. 2.1). Таке представлення можна записати як

(2.1)

Складовими вектора по базису (i, j, k) будуть вектори ,,. Коефіцієнти,,, є проекціями вектораx на координатні осі i, j, k і називаються координатами вектора x. Інакше кажучи, вектор x у тривимірному просторі повністю визначається сукупністю його координат .

Щоб перейти до узагальнення поняття вектора тривимірного простору для випадку - мірного простору, розглянемо приклад. Деяке наближене уявлення про функцію (сигнал)можна скласти з її відображення послідовністю прямокутних імпульсів, які мають на інтервалахзначення(рис. 2.2). Якщо тепер умовно представити функціюна інтервалі“вектором”, то для його визначення буде потрібнокоординат. Це означає, що функціюза аналогією з (2.1) можна подати у вигляді суми [17]

, (2.2)

де - елементарні базисні функції;.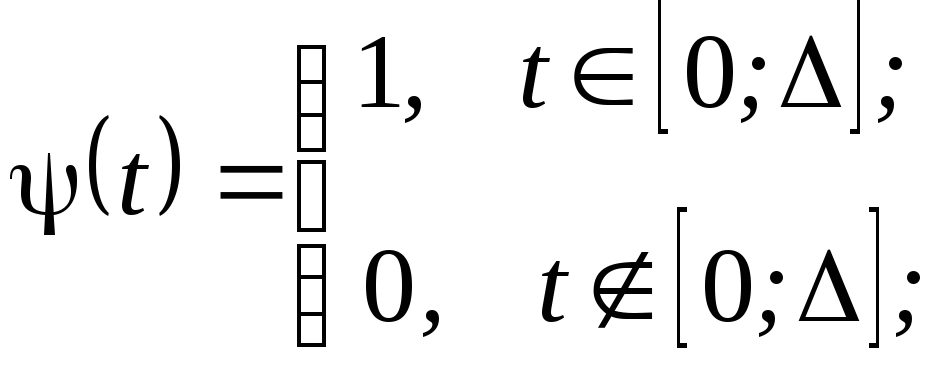

Рисунок 2.1 – Зображен­ня вектора x в тривимірній ортогональній системі коор­динат

Рис. 2.2 – Відображення неперервної функції послідов­ністю прямокутних імпульсів

Вектор x, що відповідає функції , у-вимірному просторі одиничних ортівбуде повністю визначатися його координатами . Таким чином, сигналдовільної форми набудевигляду суми найпростіших елементарних сигналів, у даному випадку у вигляді імпульсів прямокутної форми. Слово простір використовується тут, щоб надати множині сигналів геометричного змісту і тим самим наочності. Найпростішим і в той же час фізично досить змістовним є трактування сигналів як елементів нормованого лінійного метричного простору.

Лінійним або векторним називається простір, для елементів якого виконуються правила додавання і множення на будь-яке число з деякої множини , яканазивається множиною скалярів. Додавання векторів відбувається покоординатно, тобто сумою векторів x (функції ) іy (функції ) називається векторx+y, що належить даномупростору, а добуток вектораx на число дає вектор, що також належить даному простору. У лінійному просторі існує нульовий елемент 0, такий, що і кожному елементові x відповідає протилежний елемент - x, отже . Вектор, утворений додаваннямлінійно незалежних (базисних) векторівзі скалярними коефіцієнтаминазивається їхньою лінійною комбінацією.

Множина векторів називається лінійно незалежним (базисом), якщо умова

(2.3)

виконується лише тоді, коли усі . Інакше кажучи, лінійно незалежною називається множина, для якої жодна з її компонент не може бути утворена лінійною комбінацією інших. Розмірність лінійного простору визначається кількістю будь-яких лінійно незалежних базисних векторів , які утворюють цей простір. Лінійно незалежні векториможна розглядати як координатні осі простору.

Метричним називається простір, у якому визначена відстань між елементами (векторами) простору (метрика), тобто кожній парі елементів, скажемо, x і y може бути поставлене деяке дійсне невід’ємне число і спосіб, за якимзнаходиться це число. Відстань задовольняє наступні правила:

1. , якщо;

2. ;

3. ,

де ,z - елементи (точки) простору. Смисл перших двох умов очевидний. Третю умову називають нерівністю трикутника: довжина сторони трикутника менша (або дорівнює) сумі двох інших сторін.

Нормовані простори. Серед лінійних метричних просторів важливе місце займають нормовані простори. Цей вид простору визначається заданням норми , яка задовольняє наступним аксіомам:

1. ;

2. ;

3..

Спочатку наведемо терміни і визначення, які стосуються - мірного дійсного евклідового простору . Будь-який векторx у цьому просторі визначається сукупністю його координат . Сукупністьлінійно незалежних векторів утворює-мірний евклідовий простір, який позначається. Простірможна визначити як безліч точок, представлених кінцями векторів, для яких норма

.

Як бачимо, норма є узагальненням довжини вектора в двомірному і тривимірному просторі. Відстань між двома векторами x і y визначається як норма різниці векторів

.

Для простору Евкліда можна ввести поняття скалярного добутку двох векторів x і y [30]

, (2.4)

де кут між двома векторами. Для проекцій наінавпаки, на, маємо:

; .

Координати вектора являють собою проекції вектора на координатні осі, аналогічно (2.1). Зі співвідношення (2.4) випливає очевидна нерівність

, (2.5)

відома в літературі як нерівність Буняковского-Шварца. Знак рівності має місце лише тоді, коли , де – скаляр, тобто коли векториx і y колінеарні. Для відповідних сигналів іце означає, що вони збігаються за формою. Квадрат вище визначеної норми вектораx можна знайти як скалярний добуток вектора самого на себе

. (2.6)

При простір переходить у нескінченновимірний простір Гільберта, що позначається. Гільбертовим простором є, зокрема, простір усіх безперервних комплексних функцій аргументу, заданих в інтервалі, у якому скалярний добуток визначається співвідношенням [19]

, (2.7)

а квадрат норми запишемо у вигляді

.(2.8)

Норма (2.4) має не тільки геометричний, але і виразний фізичний зміст. Так, якщо сигнал – речовинний електричний струм в одиничному опорі 1Ом, то квадрат норми

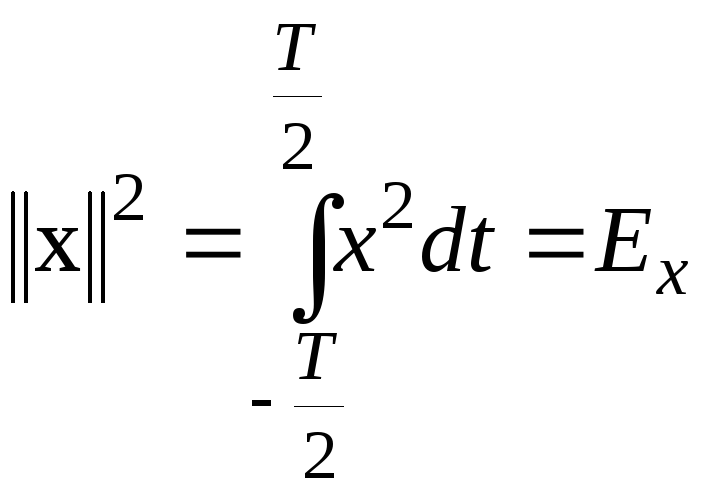
визначає енергію сигналу. Елементи гільбертового простору характеризуються квадратом, що інтегрується, тобто якщо елементи цього простору – речовинні сигнали, визначені на інтервалі, то виконується умова

. (2.9)

Гільбертовий простір позначається при цьому . Приодержуємо простір. Для деяких сигналів (функцій) просторуумова (2.5) приможе не виконуватися, але виконується умова

. (2.10)

У цьому випадку можна замість (2.10) увести скалярний добуток з розмірністю потужності (для струмів і напруг на одиничному опорі)

. (2.11)

Квадрат норми вектора x у цьому випадку запишеться у вигляді

. (2.12)

При виконанні умови (2.10) у просторі визначені і співвідношення (2.11) та (2.12) при.

Надалі, говорячи про функції з квадратом, що інтегрується, у просторі , маємо на увазі виконання умови (2.9) або умови (2.10) при. Квадрат відстані між двома векторами в речовинному просторівизначається співвідношенням

(2.13)

або

. (2.14)

Формулу (2.14) можна використовувати і при для сигналів з кінцевою середньою потужністю.

Простір являє собою природне узагальнення простору, одержуваний шляхом переходу від дискретизованої функції до функції безперервного аргументу. У курсі ТЕЗ простірмає особливе значення, тому що він дозволяє застосувати загальні геометричні уявлення до повідомлень, сигналів і завад, визначених як функції безперервного аргумента. Спрямувавши в (2.2) ,одержуємо вираз безперервної функції в просторіГілберта:

. (2.15)

У задачах перетворення повідомлень і сигналів нам будуть потрібні деякі узагальнення функціональних залежностей. Величина називається функцією незалежної змінної, якщо кожному значенню(з безлічі його можливих значень) відповідає визначене значення . Інакше кажучи, функціональна залежністьустановлює відповідність між деякою множиною чиселі множиною чиселабо, що те ж саме, функція встановлює залежність одного числа від іншого.

Більш загальним поняттям є поняття функціонала. Функціонал установлює відповідність між множиною чисел з одного боку, і деякою множиною функцій - з іншого. Можна сказати, що функціонал встановлює залежність числа від функції. Прикладом функціонала є визначений інтеграл, величина якого (при незмінних межах) залежить від виду підінтегральної функції.

Дуже корисним є поняття функціонального оператора, який встановлює відповідність між двома множинами функцій, тобто за допомогою оператора встановлюється така залежність. Через те що функції можуть бути представлені векторами і множина функцій визначається як векторний простір, дію оператора можна описати в геометричних термінах як перетворення просторуX векторів x у простір Y векторів y. Зворотне перетворення Y в X позначають . У задачах перетворення повідомлень і сигналів використовуються поряд з лінійними операторами також нелінійні і параметричні оператори.

Якщо функція на кожному інтерваліможе приймати одне зможливих значень , де , то на відрізку тривалістювона буде цілком визначеназначеннямиабо, що те ж саме, сукупністю коефіцієнтів, яка називається-набором. Зокрема, прикоефіцієнтприймає значення 0 або 1,-набір це просто кодова комбінація-значного двійкового () коду, яка відображає символ (букву, цифру) переданого повідомлення. Двійкові-набори відображаються векторами (точками) у просторі Хеммінга [24].

Скалярний добуток у цьому просторі зручно задати функцією

,

де знак – сума в звичайному розумінні. Звідси норма двійкового вектора

.

Можна бачити, що норма двійкового вектора визначається кількістю одиниць, що містяться в ньому. Цю норму називають також вагою вектора (кодової комбінації) і позначають .

Відстань у просторі Хеммінга запишеться у вигляді

,

де знак означає операцію додавання по модулю 2 (mod 2):,,,. Наведемо приклад додавання поmod 2 двох векторів:

.

Додавання і віднімання по mod 2 еквівалентні. У просторі Хеммінга відстань між двійковими векторами визначається по кількості позицій у кодовій комбінації, у яких вектори імають символи, що розрізняються [24].У розглянутому прикладі . У більш загальному випадку, якщо кількість розрізнюваних значень дорівнює, використовується різниця по модулю .