
- •Передмова
- •Методичні вказівки до виконання розрахункових завдань
- •Огляд методів інтегрування.
- •2. Метод інтегрування частинами. Якщо та функції, що мають на деякому проміжку неперервні похідні, то справедлива формула інтегрування частинами:
- •3. Найпростіші інтеграли, які містять у знаменнику
- •4. Інтегрування раціональних дробів.
- •4.1 Розглянемо випадок, коли знаменник розкладається на лише неповторні дійсні множники першого степеня.
- •5.Інтегрування тригонометричних функцій.
- •6.Інтегрування гіперболічних функцій.
- •8.Інтегрування деяких ірраціональних функцій.
- •9.Інтегрування ірраціональних функцій виду
- •Варіанти розрахункових завдань
- •Додаток.
Передмова
Метою розрахунково-графічного завдання (РГЗ) є оволодіння студентами основних прийомів та методів числення невизначених інтегралів.
Операція інтегрування є зворотною по відношенню до диференціального числення і, як будь-яка зворотна операція, є більш складною. Студент повинен оволодіти багатьма прийомами та навиками, знати стандартні методи числення деяких класів інтегралів, а також вміти пристосовувати різні штучні прийоми. Це досягається практикою, яка повинна безперервно супроводжуватись вивченням теоретичного матеріалу.
У РГЗ перед умовами задач даються короткі теоретичні відомості, які містять основні формули, означення і деякі алгоритми.
З метою надання допомоги студентам в організації самостійної роботи при виконанні РГЗ пропонується розв’язок деяких типових прикладів.
При захисті студент повинен пояснити операції що робилися при виконанні РГЗ.
Навчальний посібник містить довідковий матеріал з елементарної математики та список рекомендованої літератури.
Методичні вказівки до виконання розрахункових завдань
Поняття невизначеного інтеграла.
Функція F(x)первісною функції f(x)
на проміжку (a;b),
якщо F(x)диференційована на проміжку
(a;b)
і ![]() для всіх
для всіх
![]() .
.
Якщо F(x)
первісна функції f(x)
на проміжку (a;b),
то всяка інша первісна функції f(x)
на цьому проміжку має вигляд
![]() ,
деС
довільна стала.
,
деС
довільна стала.
Якщо F(x)
первісна функції f(x)
на проміжку (a;b)
і С
довільна стала, то множина
![]() всіх первісних функційf(x)
називається невизначеним
інтегралом функції f(x)
на цьому проміжку і
позначається символом
всіх первісних функційf(x)
називається невизначеним
інтегралом функції f(x)
на цьому проміжку і
позначається символом
![]() .
Отже, за означенням:
.
Отже, за означенням:
![]() ,
якщо
,
якщо
![]() ,
,![]() .
.
Основні властивості невизначного інтеграла.
 ;
; ;
; ;
; ,
де m
довільна стала;
,
де m
довільна стала; .
.
При знаходженні невизначених інтегралів важливу роль виконує таблиця основних інтегралів, яку слід запам’ятати.
 ,
де
,
де
 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.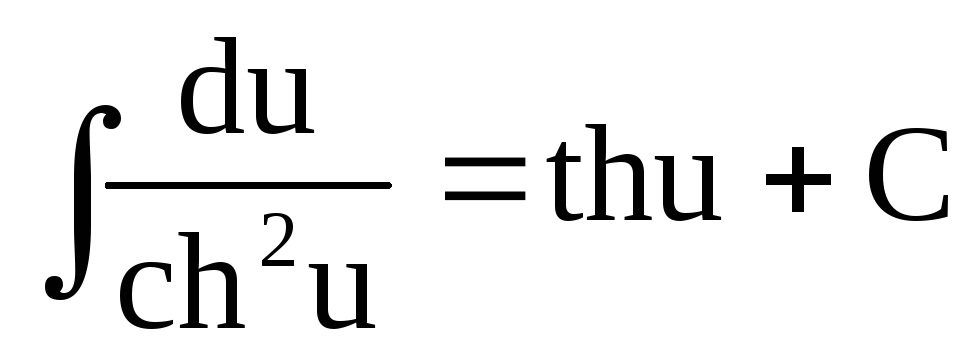 .
. .
. .
. .
. .
.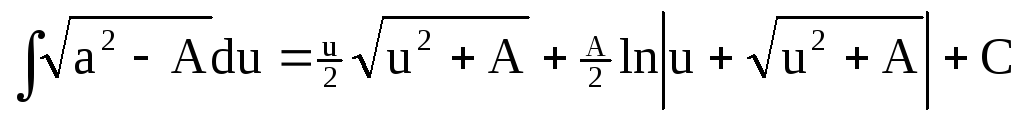 .
.
Огляд методів інтегрування.
Метод підстановки (заміна змінної).
а) Інтеграл
![]() записують у вигляді:
записують у вигляді:
![]() ,
,
тоді:

![]() .
.
У цьому разі їдеться про
“введення функції під
знак диференціала”:
![]() .
.
б) Інтеграл
![]() зображають у вигляді:
зображають у вигляді:
![]() ,
,
де функція
![]() має обернену функцію
має обернену функцію![]() і для функції
і для функції![]() відома первісна
відома первісна![]() ,
тоді:
,
тоді:

![]() .
.
У цьому разі йдеться про
“виведення функції з-під
знака диференціала”:
![]() .
.
в) Для табличних інтегралів існують такі формули:
 ;
; ;
; .
.
Приклад 1.
![]() .
.
Рішення.
![]()
 .
.
Приклад 2.
![]() .
.
Рішення.
![]()
![]() .
.
Приклад 3.

Рішення.
 .
.
Приклад 4.
![]() .
.
Рішення.
![]()
![]() .
.
Приклад 5.
![]()
Рішення.
![]()
![]() .
.
У прикладах (1-5) інтеграли обчислювалися користуючись інваріантністю формули інтегрування (підведенням під знак диференціала).
У прикладах (6-8) ми розглянемо метод заміни змінної.
Приклад 6.
![]()
Рішення.
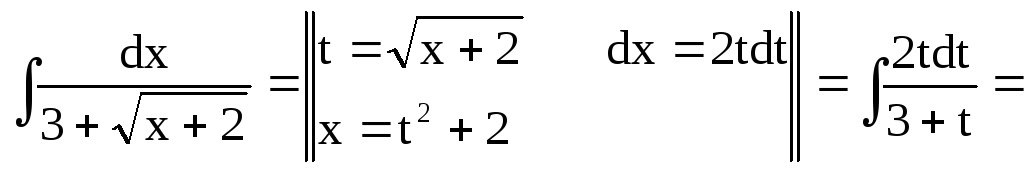
![]()
![]() .
.
Приклад 7.
![]() .
.
Рішення.
![]()
 .
.
Приклад 8.
![]() .
.
Рішення.

![]()
![]() .
.
2. Метод інтегрування частинами. Якщо та функції, що мають на деякому проміжку неперервні похідні, то справедлива формула інтегрування частинами:
![]() .
.
Методом інтегрування частинами зручно обчислювати такі типи інтегралів:
а) інтеграли виду
![]() ,
,![]() ,
,![]() ,
деP(x)
багаточлен, а
дійсне число. У цих інтегралах за u
слід взяти множник P(x),
а за
,
деP(x)
багаточлен, а
дійсне число. У цих інтегралах за u
слід взяти множник P(x),
а за
![]()
вираз, що залишився;
вираз, що залишився;
б) інтеграли виду
![]() ,
,![]() ,
,![]() ,
,![]() ,
деP(x)
багаточлен. У цих інтегралах слід взяти
за
,
деP(x)
багаточлен. У цих інтегралах слід взяти
за
![]() ;
;
в) інтеграли виду
![]() ,
,![]() ,
,![]() ,
,![]() ,
деk і
дійсні числа. В даному випадку після
застосування формули інтегрування
частинами утворюється лінійне рівняння
відносно шуканого інтеграла. Розв’язуючи
це рівняння, знаходять інтеграл.
,
деk і
дійсні числа. В даному випадку після
застосування формули інтегрування
частинами утворюється лінійне рівняння
відносно шуканого інтеграла. Розв’язуючи
це рівняння, знаходять інтеграл.
Приклад 9.
![]() .
.
Рішення.

![]() .
.
Приклад 10.
![]() .
.
Рішення. 
![]() .
.
Приклад 11.
![]() .
.
Рішення.

![]() .
.
Приклад 12.
![]() .
.
Рішення.

![]() .
.
Приклад 13.
![]() .
.
Рішення.

![]()
![]() .
.
Часто метод інтегрування частинами застосовується разом з методом заміни змінної.
Приклад 14.
![]() .
.
Рішення. 
![]()

![]() .
.
Розглянемо інтеграли, які при застосуванні формули інтегрування частинами утворюють лінійне рівняння відносно шуканого інтеграла.
Приклад 15.
![]() .
.
Рішення.Позначимо шуканий інтеграл через I.

![]()
![]() .
.
Таким чином, одержали рівняння відносно шуканого інтеграла I. Розв’язавши це рівняння:
![]() ,
,
одержимо:
![]() .
.
Такі інтеграли можна також розв’язувати методом заміни змінної (про це мова піде далі).
Розглянемо ще один зворотній інтеграл.
Приклад 16.
![]() .
.
Рішення. Як і в попередньому випадку позначимо шуканий інтеграл через I.


![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
