Глава 1. Численные методы математической физики

1.1. Основные понятия

1.1.1. Классификация дифференциальных уравнений в частных производных

Дифференциальные уравнения в частных производных имеют широкие приложения в математической физике, гидродинамике, акустике и других областях знаний. В большинстве своем такие уравнения в явном виде не решаются. Поэтому широкое распространение получили методы приближенного их решения, в частности, метод сеток.

Мы уделим основное внимание вопросу решения линейных дифференциальных уравнений второго порядка. Построение различных схем метода сеток в случае уравнений в частных производных зависит от типа уравнений и вида граничных условий. Сделаем несколько замечаний о классификации линейных дифференциальных уравнений второго порядка.

1

(1.1)

(1.2)

(1.3)

.Волновое уравнение

К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т. д. Это уравнение является простейшим уравнением гиперболического типа.

2. Уравнение теплопроводности (диффузии)

К исследованию этого уравнения приводит рассмотрение процессов распространения тепла, диффузии жидкости и газа, некоторые вопросы теории вероятностей и т. д. Это уравнение параболического типа.

3.Уравнение Лапласа

К исследованию этого уравнения приводит рассмотрение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики, диффузии и т. д. Это уравнение является простейшим уравнением эллиптического типа.

Приступим теперь к изучению конечно-разностных методов решения уравнений в частных производных.

Как правило, аналитические методы решения уравнений в частных производных связаны с разделением переменных (метод Фурье). Использование этого метода встречает большие трудности, если область независимых переменных, где находится решение, отличается от простейших (прямоугольник, круг). Вторым препятствием для применения метода Фурье является зависимость коэффициентов линейного уравнения от времени и пространственных переменных. Например, зависимость коэффициента а = a(t, x) в волновом уравнении с функцией a(t, x) достаточно общего вида уже не позволит разделить переменные.

Отмеченные ограничения применения аналитических методов привели, особенно с развитием вычислительной техники, к широкому распространению численных методов решения уравнений с частными производными. Опыт решения многих сложных задач науки и техники численными методами подтверждает их эффективность.

Уравнения (1.1), (1.2), у которых одна из независимых переменных t является временем, называются нестационарными. Уравнение (1.3) для функции и(х,у), зависящей только от пространственных координат х и у, является стационарным.

1.1.2. Аппроксимация частных производных

Первым этапом в численном решении дифференциальных ypaвнений с частными производными является переход от непрерывной задачи к дискретной. Дискретизация задачи – это основа численного метода.

Рассмотрим некоторые конечно-разностные аналоги частных производных от функции и по переменным х, у, t, подобно случаю обыкновенных дифференциальных уравнений, с учетом той особенности, что теперь имеются две независимые переменные. Начнем с того, что рассмотрим разности только в направлении х. Вспомним, что разложение Тейлора функции и(х + h, у) в окрестности точки (х, у) можно записать в виде

(1.4)

(1.5)

(1.6)

(1.7)

(1.8)

(1.9)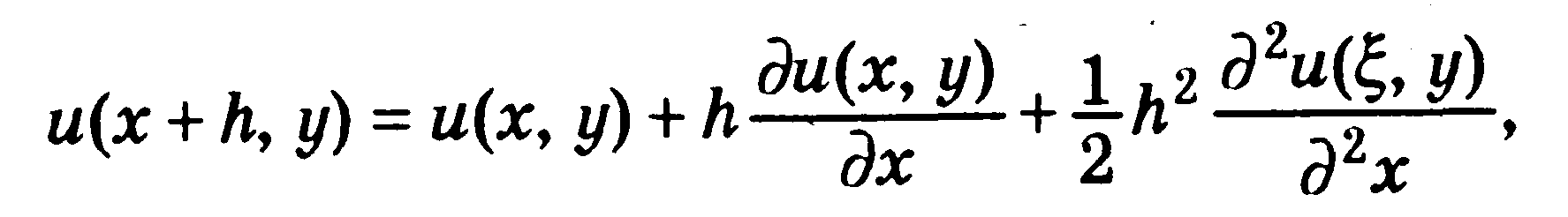

где ξ лежит между х и х + h.

Из последнего равенства получаем

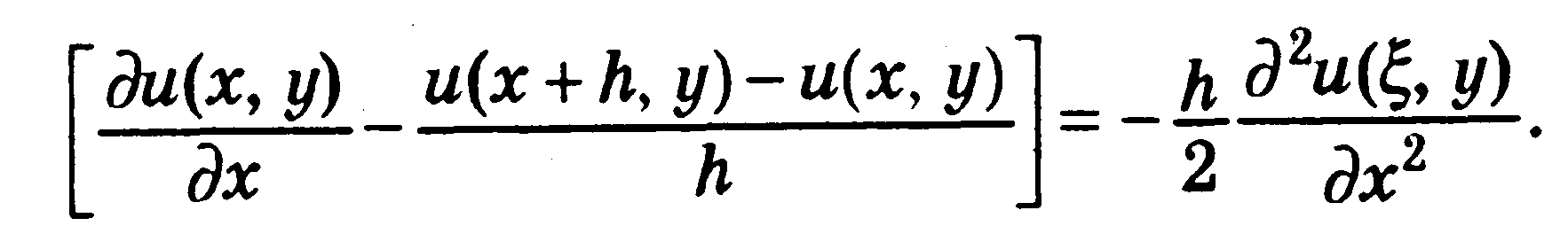
Таким образом, если представить и_x с помощью равенства

то погрешность аппроксимации (дискретизации) или погрешность ограничения будет равна

где x<ξ<x+h.

В формуле (1.5) частная производная и_x выражена через правую конечную разность [u(x+h, у) – и(х, y)]. Выразим и_x через левую разность [u(x, y) - u(x-h, y)]. Для этого в разложение Тейлора вместо (х + h) подставим (х - h)

где (x - h)<ξ<x.

При этом получаем приближенное равенство

которое выполняется с погрешностью, равной:

где (х - Н)<ξ<х.

В последствии нам потребуются и правая (1.5) и левая (1.8) разности.

Теперь получим разностное приближение для u_xx=д²u/дx². Если и(х, у) имеет частные производные до четвертого порядка включительно, тогда разложение Тейлора функций и(х + h, y), u(х - h, y) в окрестности точки (х, y) можно записать в виде

где х < ξ < (х + h),

где (х - h) < ξ < х.

Сложив два последних равенства, получим

(1.10)

которое выполняется с точностью

где (х – h)<ξ<(х + h).

Здесь рассмотрены производные в направлении х. Совершенно аналогичный анализ можно провести для производных в направлении у и получить формулы, аналогичные формулам (1.4) – (1.11). Используя эти выражения, можно представить дифференциальные уравнения в частных производных (1.1) – (1.3) через конечно-разностное приближение (конечно-разностные схемы).