3.3.Частотные критерии устойчивости Михайлова и Найквиста

Частотные критерии устойчивости основываются на использовании принципа аргумента. Рассмотрим этот принцип, для чего характеристический полином замкнутой системы

(3.13)

в соответствие с теоремой Безу представим в виде:

F(p) = , (3.14)

где p_i – полюс передаточной функции замкнутой системы ().

Поставляя в выражение (3.13) вместо p комплексную переменную jω, получим:

. (3.15)

После аналогичной подстановки в выражение (3.14) получим:

F( jω) = . (3.16)

Каждому сомножителю в выражении (3.16) на комплексной плоскости соответствует некоторый вектор, положение которого меняется при изменении ω.

Определим изменение аргумента комплексной функции F(jω) при изменении частоты ω от 0 до . Для этого необходимо определить изменение аргумента каждого из векторов, поскольку

F(jω) = ∑(jω – p_i).

Если корень характеристического уравнения p_i действительный и отрицательный, т.е. рас­положен на действительной оси слева от начала координат (рис. 3.4, а), то вектор поворачивается против часовой стрелки на угол π/2, если этот ко­рень действительный и положительный (рис. 3.4, б), то вектор поворачивается по часовой стрелке на угол π/2. Следовательно, для левого действительного полюса

= π/2,

а для правого действительного полюса

= – π/2,

Нетрудно показать, что для пары комплексно сопряженных левых полюсов (рис. 3.4, в) изменение аргумента составляет +π, а для пары комплексно сопряженных правых полюсов (рис. 3.4, г) равно -π.

Если среди n полюсов передаточной функции замкнутой системы m расположены справа от мнимой оси, а остальные (n – m) – слева, то изменение аргумента комплексной функции F(jω) вектора равно:

F(jω) = (n – m)∙ π/2 – m∙π/2 = (n – 2m)∙π/2. (3.17)

Выражение (3.17) и определяет суть принципа аргумента. В передаточной функции устойчи­вой системы правые полюса отсутствуют, т.е. m = 0, и изменение аргумента F(jω) равно:

F(jω) = n∙π/2. (3.18)

Из выражения (3.18) следует критерий устойчивости Михайлова, согласно которому из­менение аргумента комплексной функции F(jω) определяется по годографу, который записывают в виде

F(jω) = Х(ω) + jY(ω) ,

где Х(ω),Y(ω) – действительная и мнимая составляющие комплексной функции F(jω);

Х(ω) = a₀ – a₂ω² + a₄ω⁴ – a₆ω⁶ + ……;

Y(ω) = a₁ω – a₃ω³ + a₅ω⁵ – a₇ω⁷ + …….

Каждому значениюω = ω_i на комплексной плоскости соответствует точка с координатами ( Х(ω_i),Y(ω_i) ). При изменении ω эта точка описывает на плоскости некоторую траекторию, которая называется годографом Михайлова (рис. 3.5).

При ω = 0 Х(0) = a₀, Y(0) = 0, т.е. F(0) = a₀, причем в соответствии с выражением (3.6) a₀ > 0.

Формулировка критерия Михайлова: замкнутая система устойчива, если годограф F(jω), начинаясь при ω = 0 на положительной дей­ствительной полуоси, при изменении ω от 0 до обходит последовательно в положитель­ном направлении (против часовой стрелки)n квадрантов, где n – порядок системы.

Только в этом случае выполняется условие (3.18). На рис. 3.5, а,б, приведены примеры годографов для устойчивых и неустойчивых систем. Если годограф про­ходит через начало координат (рис.3.5, в), то система находится на границе устойчивости.

Из формулировки критерия следует, что система устойчива, если годограф Михайлова, начавшись на действительной оси при ω = 0, несколько раз последовательно пересекает действительную и мнимую ось. Значения ω, при которых происходят эти пересечения, являются действительными положительными корнями уравнения Y(ω) = 0 (при пересечении с действительной осью) и уравнения Х(ω) = 0 (при пересечении с мнимой осью). Следовательно, оценить устойчивость системы можно и без построения годографа: достаточно, чтобы корни указанных уравнений чередовались друг с другом.

На практике более широ­кое применение, по сравнению с критерием Михайлова, нашел частотный критерий Найквиста, который позво­ляет судить об устойчивости замкнутой системы по частотным характеристикам этой системы в разомкнутом состоянии.

Рассмотрим замкнутую систему с единичной обратной связью. Первоначально будем полагать, что соответствующая ей разомкнутая система устойчива. Пусть передаточная функция этой системы в разомкнутом состоянии

W(p) =

имеет n-й порядок, т.е. число ее полюсов (порядок полиномаA(р)) равноn. На основании принципа физической реализуемости можно утверждать, что число нулей передаточной функцииW(p) (порядок полиномаВ(р)) не превышает n. Передаточная функция системы в замкнутом состоянии:

Ф(р) ==.

Введем в рассмотрение выражение:

D(p) =1 +W(p) = .(3.19)

Очевидно, что число нулей и полюсов выражения D(p) одинаково и равно n. При этом числитель выражения (3.19) является характеристическим полиномом замкнутой системы, а знаменатель – характерис­тическим полиномом разомкнутой системы. Осуществим в выражении (3.19) замену p на jω:

D(jω) = (3.18)

и определим из­менение аргумента (3.20), полагая, что замкнутая система устойчива. Поскольку в этом случае в соответствии с принципом аргумента

В(jω) = n∙π/2 и (А(jω) + В(jω)) = n∙π/2,

то

D(jω) = (А(jω) + В(jω)) – В(jω) = 0.

Таким образом, если разомкнутая и замкнутая систе­мы устойчивы, то изменение аргумента D(jω) равно нулю, следовательно, годограф D(jω) не охватывает начала координат (рис. 3.6, а).

В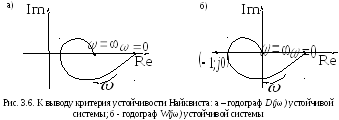противном случае, когда годограф охватывает начало координат, изме­нение его аргумента не равно нулю и система в замкну­том состоянии неустойчива.

Очевидно, что об изменении аргумента вектора удобнее судить не по годографу D(jω) , а по годографу амплитудно-фазовой характеристики разомкнутой системы W(jω). Поскольку D(jω) = 1 + W(jω), изменение аргумента D(jω) будет рав­но нулю, если годограф амплитудно-фазовой характе­ристики разомкнутой системы не охватывает точку с ко­ординатами (-1, j0) (рис. 3.6, б).

Отсюда следует формулировка критерия Найквиста: система, устойчивая в разомкнутом состояние, будет устойчива и в замкнутом состоянии, если годограф амплитудно-фазовой характеристики разомкнутой системы не охва­тывает точку с координатами (-1, j0). В том случае, когда годограф частотной характеристики охватывает эту точку, система неустойчива.

Если САУ содержит ν интегрирующих звеньев, то начальное значение фазочастотной характеристики разомкнутой системы равно (-ν∙π/2), а амплитудно-частотной – бесконечности. Поэтому,

• если ν =1, характеристика W(jω) при ω → 0 уходит в бесконечность вдоль отрицательной мнимой полуоси;

• если ν = 2 – вдоль отрицательной действительной полуоси;

• если ν = 3 – вдоль положительной мнимой полуоси.

Для удобства оценки устойчивости таких астатических систем годограф W(jω) дополняют дугой бесконечного радиуса, начинающейся на положительной действительной полуоси и проводимой до пересечения с годографом W(jω) (рис. 3.7). Формулировка критерия устойчивости при этом не изменяется.

Если годограф W(jω) разомкнутой системы проходят через точку (1, j0), то система в замкну­том состоянии находится на границе устойчивости.

Рассмотрим случай, когда система в разомкнутом состоянии неустойчива и имеет m правых полюсов. Полагая, что при замыкании обратной связи система становится устойчивой, в соответствии с принципом аргумента получаем:

В(jω) = (n –2m)∙π/2 и (А(jω) + В(jω)) = n∙π/2,

При этом изменение аргумента D(jω) равно:

D(jω) = (А(jω) + В(jω)) – В(jω) = n∙π/2 – (n –2m)∙π/2 = m∙π = 2π∙ m/2.

Следовательно, система в замк­нутом состоянии будет устойчивой, если годограф час­тотной характеристики D(jω) m/2 раз охватывает начало координат, а соответственно годограф амплитудно-фазовой характе­ристики разомкнутой системы W(jω) m/2 раз охва­тывает точку с координатами (-1,j0), где m – число правых полюсов разомкнутой системы.

Годограф амплитудно-фазовой характеристики W(jω) реальной технической системы может иметь достаточно сложную форму (рис. 3.8).

Вэтом случае сложно определить, сколько раз годографW(jω) охватывает начало координат. Задача упрощается, если ввести в рассмотрение понятие перехода годографа W(jω) через действительную ось, т.е. пересечение графиком W(jω) действительной оси левее точки с координатами (-1, j0). Перехода годографа W(jω) через действительную ось считается положительным, если при увеличении частоты ω пересечение оси происходит сверху вниз (годограф переходит из второго квадранта в третий), в противном случае переход считается отрицательным.

Обозначим число положительных переходов m₊ , а число отрицательных переходов m_- . Тогда критерий устойчивости Найквиста может быть сформулирован так: система в замк­нутом состоянии становится устойчивой, если разность между числом положительных и отрицательных переходов равна m/2, т.е.

m₊ – m_- = m/2, (3.21)

где m – число правых полюсов разомкнутой системы.

Если система в разомкнутом состоянии устойчива (m = 0) условие устойчивости системы при ее замыкании упрощается:

m₊ – m_- = 0. (3.22)