Омский государственный технический университет

Кафедра

«Средства связи»

Лабораторная работа №1-5 по курсу

«Теория электрической связи»

«ИССЛЕДОВАНИЕ СПЕКТРА СИГНАЛОВ С ЧАСТОТНОЙ МОДУЛЯЦИЕЙ»

100000000000000000000000000000000000000000000

Выполнил: студент

группы РП-219

Кучер Дмитрий

Проверил: с.н.с., к.т.н.,

доцент Хазан В.Л.

Омск 2011

ЦЕЛИ РАБОТЫ:

1. Исследование посредством имитационного моделирования состава спектра сигнала при модуляции частоты несущего колебания гармоническим колебанием;

2. Исследование зависимости амплитуд спектральных составляющих модулированных по частоте сигналов от девиации частоты;

3. Исследование посредством имитационного моделирования характера спектра манипулированных по частоте сигналов от девиации частоты и периода манипулирующей периодической последовательности прямоугольных импульсов типа "меандр";

4. Сравнение результатов имитационного моделирования с результатами аналитических расчетов.

Теоретические сведения.

Частотно-модулированные сигналы.

Р ассмотрим наиболее простой случай, когда модулирующий сигнал является низкочастотным гармоническим колебанием. На рис. 1-5.1(а) приведена осциллограмма такого рода колебания. На рис. 1-5.1(b) показана осциллограмма высокочастотной (не модулированной) несущей. На рис.1-5.1(с) изображено частотно-модулированное (ЧМ) колебание.

Рис. 1-5.1.

На рис. 1-5.1 обозначено: Um(t) - модулирующее колебание; Am - амплитуда модулирующего колебания; Т - период модулирующего колебания; Un(t) - несущее колебание; Аn - амплитуда несущего колебания; t - период несущего колебания.

Сигналы с угловой модуляцией описываются выражением:

(1-5.1)

(1-5.2)

В случае частотной модуляции: (1-5.3)

Здесь f_o = 1/t, а f(t) - отклонение мгновенной частоты от среднего значения.

Если модулирующее колебание является гармоническим, как в случае, изображенном на рис. 1-5.1 (а), то оно описывается выражением:

где F_m = 1/T, а Ф_m - начальная фаза этого колебания.

Тогда, согласно (1-5.3),

(1-5.4)

Здесь f_d - девиация частоты.

В результате частотно-модулированное колебание можно описать выражением:

(1-5.5)

Отношение m = f_d/F_m в выражении (1-5.5) называют индексом угловой модуляции.

Для простоты, считая начальные фазы модулирующего и несущего колебаний равными нулю (Ф_m = 0 и j_n = 0), и раскрывая при этом условии выражение (1-5.5), имеем:

(1-5.6)

Функции cos[msin(2F_mt)] и sin[msin(2F_mt)]являются периодическими и могут быть представлены в виде рядов Фурье:

(1-5.7)

(1-5.8)

Здесь J_n(m) - функции Бесселя (цилиндрические функции) 1-го рода n-го порядка от действительного аргумента. ( Буква J читается как "йот" или "жи").

Графики такого рода функций Бесселя 0-го, 1-го, 2-го и 3-го порядков изображены на рис. 1-5.2 сплошными линиями. На этом же рисунке пунктирной линией приведен график функции Бесселя 16-го порядка. Из рис. 1-5.2 видно, что начиная со второго порядка чем больше порядок функции Бесселя, тем при больших значениях аргумента эта функция становится заметно отличной от нуля. Например, J₁₆(11) = 0,005, J₁₆(12) = 0,014 и т. д.

Рис. 1-5.2

Выражение (1-5.6) с учетом (1-5.7) и (1-5.8) можно преобразовать к виду:

(1-5.9)

Из выражения (1-5.9) следует, что амплитуда k-ой (по отношению к нулевому компоненту на частоте несущего колебания) составляющей спектра ЧМ сигнала равна произведению амплитуды несущего колебания A_n на функцию Бесселя J_k(m).

Согласно (1-5.9) в самом общем случае спектр частотно-модулированного гармоническим колебанием сигнала содержит бесконечно большое число компонентов. Однако с учетом того, что функции Бесселя больших порядков для малых аргументов фактически не отличаются от нуля, спектры реальных сигналов располагаются практически на ограниченных интервалах оси частот. Так, например, для частного случая, когда m<<1, с учетом того, что J₁(m) " m/2 и J_o(m) " 1, для частотно-модулированного колебания справедливо приближенное равенство:

(1-5.10)

То есть при очень малых индексах угловой модуляции заметными остаются всего три компонента из общего числа всех составляющих спектра частотно-модулированного гармоническим колебанием сигнала. Таким образом, в этом случае количественно спектр ЧМ сигнала не будет отличаться от спектра АМ сигнала, исследуемого в лабораторной работе 1-4. Однако фаза верхней боковой составляющей спектра ЧМ сигнала отличается от фазы верхней боковой составляющей спектра АМ сигнала на 180 градусов.

С увеличением индекса угловой модуляции m=f_d/F_m (либо с увеличением девиации частоты f_d, либо с уменьшением частоты модулирующего сигнала F_m) спектр ЧМ сигнала в соответствии характером поведения функций Бесселя (см. рис. 1-5.2) расширяется и содержит число компонентов приблизительно равное удвоенному значению индекса модуляции m. Т. е. можно считать, что полоса частот F, занимаемая спектром ЧМ сигнала, может быть приближенно оценена

следующим образом: F"2m/T =2mF_m=2f_d. Отсюда следует вывод о том, что при больших значениях индекса угловой модуляции m полоса частот F, занимаемая спектром ЧМ сигнала, приблизительно равна удвоенному произведению индекса угловой модуляции и частоты модулирующего колебания или удвоенному значению девиации частоты.

Н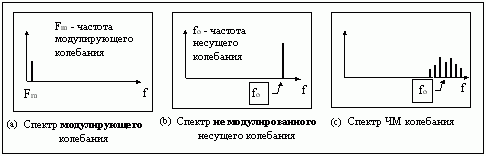 а рис. 1-5.3 приведены спектрограммы, которые соответствуют сигналам, изображенным на рис. 1-5.1.

Рис. 1-5.3.

Манипулированные по частоте сигналы.

На рис. 1-5.4(а) приведена осциллограмма манипулирующей последовательности прямоугольных видеоимпульсов. На рис. 1-5.4(b) показана осциллограмма высокочастотной (не манипулированной) несущей. На рис. 1-5.4(с) изображено частотно-манипулированное колебание.

Отношение периода последовательности импульсов Т к длительности одного импульса Т_и называется скважностью: q=T/T_и.

Частотно-манипулированные сигналы называют часто ЧТ-сигналами, потому что они используются в частотной телеграфии.

Определим спектр манипулирующей последовательности.

Постоянная составляющая периодической последовательности видеоимпульсов U_o равна площади одного импульса, усредненной на периоде:

(1-5.11)

Коэффициенты ряда Фурье можно определить с помощью известных выражений:

(1-5.12)

Амплитуда n-ой гармоники периодической последовательности видеоимпульсов равна:

(1-5.13)

Разница частот f соседних спектральных составляющих обусловлена периодом последовательности T и равна f=1/T. Из выражения (1-5.13) следует, что первый минимум огибающей спектра зависит от длительности видеоимпульсов и имеет значение f₁ = 1/Tи.

Количество спектральных гармонических компонентов, расположенных в пределах основного лепестка sinc-функции, равно скважности манипулирующей периодической последовательности.

Частотно-манипулированный сигнал описывается выражением:

(1-5.14)

Очевидно, что этот сигнал можно представить как два амплитудно-манипулированных колебания, одно из которых с частотой (fo + fd) манипулировано по амплитуде обычным способом, а второе c частотой (fo - fd) - инверсированным колебанием:

(1-5.15)

С учетом результатов исследования, полученных в лабораторной работе 1-4, можно утверждать, что спектр модулирующего колебания одновременно переносится на частоты (fo + fd) и (fo - fd).

На рис. 1-5.5 приведены спектрограммы, которые соответствуют сигналам, изображенным на рис. 1-5.4.

Рис. 1-5.4

Имитационные модели.

Н а рис. 1-5.6 приведена блок-схема имитационной модели, посредством которой проводятся исследования при частотной модуляции гармоническим колебанием. Анализатор спектра реализован на принципах дискретного преобразования Фурье.

Рис. 1-5.6

Н а рис. 1-5.7 приведена блок-схема имитационной модели, посредством которой проводятся исследования при частотной манипуляции сигнала периодической последовательностью видеоимпульсов типа "меандр".

Рис. 1-5.7