2. Двоїстий симплекс-метод

Оцінками плану прямої задачі є рядок , а оцінками плану двоїстої – стовпчик «План» з компонентами вектора вільних членів системи обмежень В.

Двоїстий симплекс-метод:

Нехай необхідно розв’язати задачу лінійного програмування, подану в канонічному виді:

, (1)

, (2)

. (3)

Тоді двоїстою до неї буде наступна задача:

, (4)

. (5)

Нехай, початковий базис складається з m векторів , причому хоча б одна з компонент вектора від’ємна.

Нехай , однак за критерієм оптимальності плану, всі оцінки векторів .

На підставі першої теореми двоїстості план двоїстої задачі відшукуємо у вигляді: . Цей план не є оптимальним для прямої задачі, оскільки він не задовольняє умову невід’ємності змінних (3) і не є оптимальним для двоїстої задачі, бо всі оцінки векторів оптимального плану двоїстої задачі мають бути невід’ємними.

Отже, вектор, що відповідає компоненті , потрібно виключити з базису початкової задачі, а вектор двоїстої задачі, що відповідає від’ємній оцінці, включити до базису двоїстої.

У прямому симплекс-методі спочатку виявляють змінну, яку слід ввести у базис, а в двоїстому симплекс-методі навпаки — спочатку визначають змінну, яку виключають з базису, а потім змінну, яку вводять у базис.

Алгоритм двоїстого симплексного методу:

1. Необхідно звести всі обмеження задачі до виду « », ввести додаткові невід’ємні змінні, визначити початковий базис та перший опорний план .

2. Якщо всі оцінки векторів і компоненти вектора-стовпчика «План» для всіх , то задача розв’язана.

Інакше необхідно вибрати найбільшу за модулем компоненту і відповідну змінну виключити з базису.

3. Якщо в і-му рядку, що відповідає змінній , не міститься жодного , то цільова функція двоїстої задачі необмежена на багатограннику розв’язків, а початкова задача розв’язку не має. Інакше існують деякі і тоді для відповідних стовпчиків визначають аналогічно прямому симплекс-методу оцінки :

( ),

що дає змогу вибрати вектор, який буде включено в базис.

4. Виконавши крок методу повних виключень Жордана-Гаусса, переходять до наступної симплексної таблиці (Переходять до пункту 2).

Приклад 2.

Знайти мінімальне значення функції:

,

за умов:

.

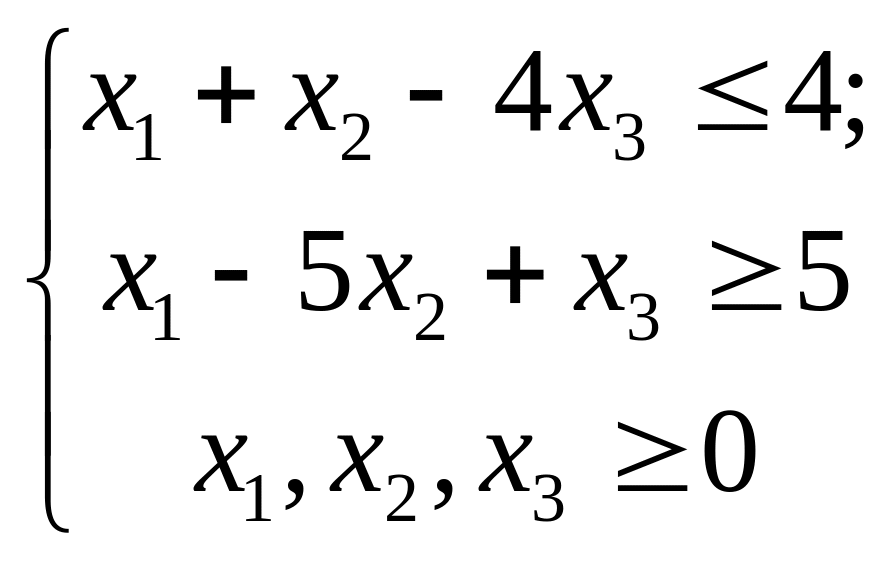Розв’язання:

Помножимо другу нерівність на (– 1) і введемо додаткові змінні.

Початковий базис: вектори А₄ та А₅.

Псевдоплан: .

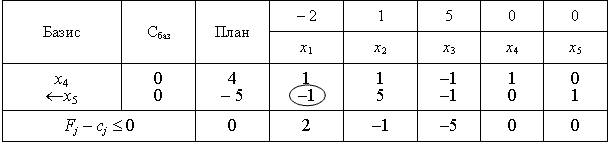
- тому виведемо вектор А₅ і змінну х₅.

Введемо – на основі розрахунку значення :

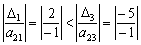, = ввести вектор А1. Розв’язувальним елементом буде а₂₁ (–1).

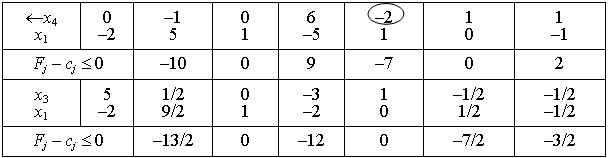
Оптимальний план початкової задачі:

,

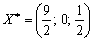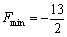
та оптимальний план двоїстої задачі:

, .

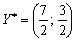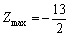3. Метод відтинаючих площин (метод Гоморі)

варіанти:

1. Перший алгоритм Гоморі для рішення повністю цілочисельних задач.

2. Другий алгоритм Гоморі для рішення частково цілочисельних задач.

Ідея розрахунків методом відтинаючих площин для розв’язання повністю цілочисельних задач (1-й метод Гоморі) полягає у такому підході:

1. лінійна задача 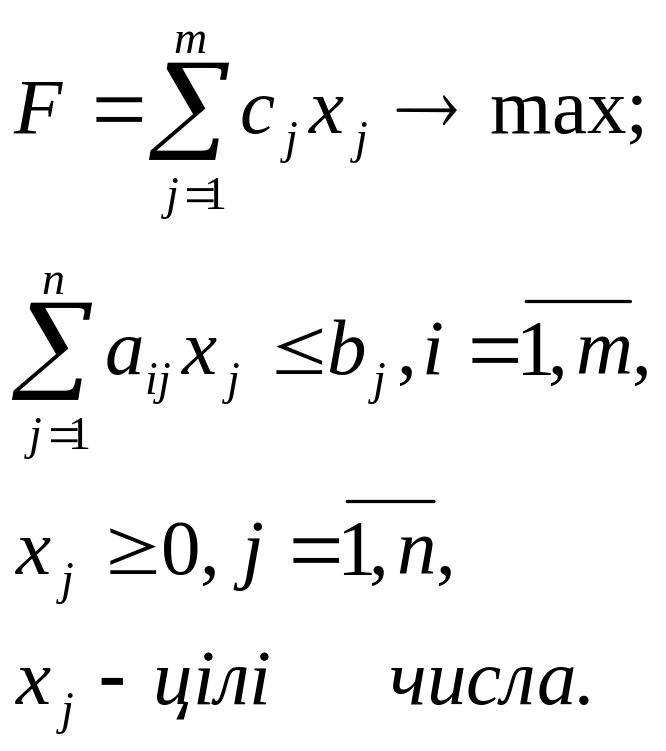(1)

(1)

Опорний план, який має канонічний вигляд:

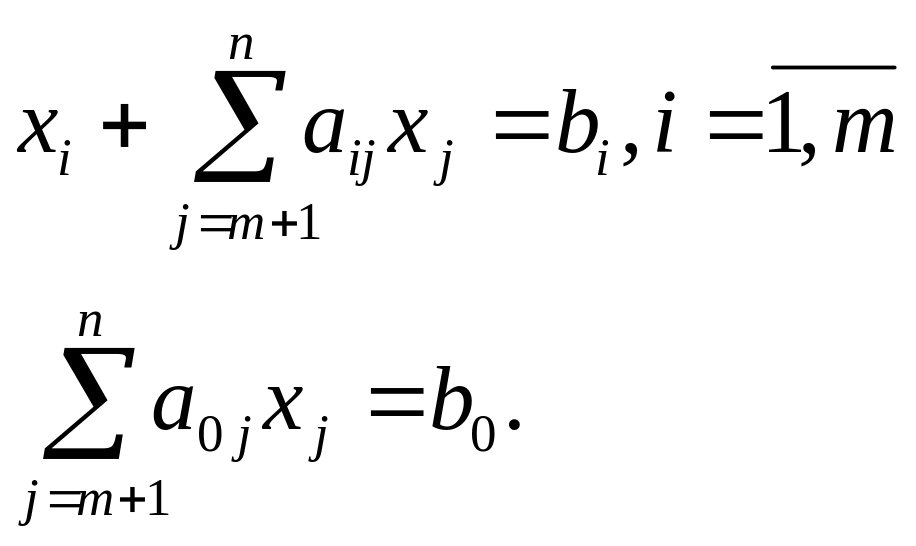(2)

2. якщо серед рівнянь-обмежень (2) є дробові значення базисних змінних x_i = b_i, то обирають серед них таке значення, яке має найбільшу дробову частину. Це рівняння

Перетворюють у додаткову нерівність:

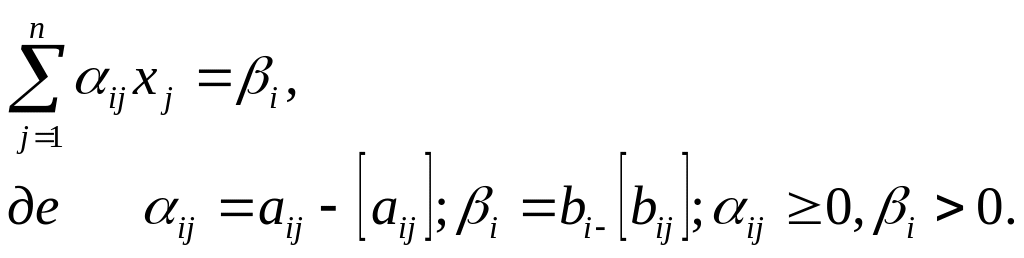(3)