
❶Матрица – система m-n чисел, расположенных в прямоугольной таблице из м-строк и n-столбцов.
Числа этой таблицы – элементы матрицы
Равные матрицы – матрицы, у которых совпадает количество строк и столбцов
Матрица, состоящая из одной строки называется – строчной
Матрица состоящая из одного столбца называется - столбцевой
Порядок матрицы – число строк или столбцов
Диагональная
матрица –
квадратная матрица, у которой все
элементы, не принадлежащие главной
диагонали равны нулю А=
Единичная матрица – диагональная матрица, у которой все элементы главной диагонали равны 1
А=
❷ Действия над матрицами
1)Сложение(происходит поэлементно)
А= В=
В= С=А+В=
С=А+В=
2)Вычитание (поэлементно)
3)Умножение матрицы на число
λА
=
Линейные операции над матрицами обладают линейными свойствами
А + В = В + А
(А + В) + С = А + (В + С)
А + О = А
А + (-А) = О
4) умножение матриц(Для согласованных)
Матрица А называется согласованной с матрицей В если числ столбцов матрицы А равно числу строк матрицы В
Следует помнить из согласованности матрицы А с матрицей В не следует согласованность матрицы В с матрицей А
Если матрицы А и В – квадратные матрицы одного порядка, то они взаимно согласованны
А*В = В*А если это выполняется то матрицы А и В наз. перестановочными или комутотивными
Свойства умножения матриц
1) (А*В)*С = А(В*С)
2) λ(А*В) = (λ*А)В
3) (А+В)*С = АС + ВС
4) С (А+В) = СА + СВ
❸Определителем квадратной матрицы 2-порядка наз. число равное
А= =а11*а22 – а21*а12
(Δ,det) Определителем (Δ) квадратной матрицы 3-порядка наз. число
Правило Сарриоса

Свойства определителей
1)если в матрице какая-либо строка или столбец состоит из нулей, то определитель равен 0
2)при перестановке 2-х строк определитель меняет знак на противоположный
3)определитель, содержащий 2 одинаковые строки равен 0
4)общий множитель элементов строки можно выносить за знак определителя
❹ Минором какого-либо элемента определителя наз. – определитель, полученный из данного вычеркиванием той строки и того столбца, которым принадлежит данный элемент
 М21
М21

Алгебраическим
дополнением элемента aik
определителя
наз. – его минор, взятый со знаком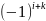
Матрицей, обратной квадратной матрице А наз. – квадратная матрица В, удовлетворяющая равенство АВ=ВА=Е
❻ Обратная матрица может существовать только для квадратной матрицы и обе матрицы имеют один и тот же порядок
Матрицу
, обратную матрице А обозначают
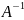
= *C
C
- присоединенная матрица
*C
C
- присоединенная матрица
А * = * А = Е
Практическое применение обратной матрицы широко используется при решении систем уравнений, неравенств, которым приводят практические задачи, а также задачам факторного анализа
❺ Ранг матрицы – наибольший из порядков ее миноров, отличных от нуля
❼Решением системы наз. такой набор чисел (), что при его подстановке в систему вместо соответствующих неизвестных каждое уравнение системы обращается в тождество.
Если система имеет хотя бы одно решение она наз. совместной
Система , не имеющая ни одного решения, наз. – несовместной
Система наз. определенной если она имеет единственное решение
Неопределенной, если она имеет более одного решения.
В этом случае каждое решение наз. частным решением системы.
Совокупность всех частных решений наз. общим решением.
Решить систему – это значит выяснить совместна она или несовместна ,если она совместна – найти общее решение
Две системы наз. эквивалентными (равносильными) если они имеют одно и тоже общее решение.
Систему можно записать в матричном виде
А*Х=В
А= - матрица системы( коэффициенты из
неизвестных
- матрица системы( коэффициенты из
неизвестных
Х=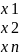 - матрица неизвестных
- матрица неизвестных
B=
 - столбец свободных членов
- столбец свободных членов
Расширенная матрица
 =
=
В туристической деятельности может быть достаточно большое число неизвестных которое при заданных условиях записываются в виде управлений
Основные методы решения систем линейных уравнений
1)Метод Крамера
2)Решение систем с помощью обратной матрицы
Х
=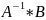
3)Метод Гаусса
❽ Метод Гаусса
Одним из наиболее универсальных и эффективных методов решения линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных
Процесс решения по методу Гаусса состоит из 2х этапов:
1)«прямой ход» - система приводится к ступенчатому виду (треугольник)
2)«обратный ход» - идет последовательное определение неизвестных из этой ступенчатой системы
Практическая направленность использования основ линейной алгебры в сфере туризма и гостеприимства.
Практические задачи связаны с линейным программирование и ранее изученными методами решения систем линейных уравнений. Методы линейного программирования были положены в 1939г. Контаровичем. Этот метод связан с проблемами планирования производства, расходами сырья.
❾ Метод Крамера
Если определитель системы отличен от нуля, то система наз. невырожденной
Пусть задана система уравнений с n-неизвестными и она записана в матричном виде (А*Х=В)
Если Д-определитель матрицы А не равен нулю, то система совместна и определенна.
Ее решение задается формулой
 *В
*В
Другую форму записи этого утверждения дают формулы Крамера
 =
=
Х= 1,2….n
 - определитель
получающийся из Д заменой
- определитель
получающийся из Д заменой
 1-ого
столбца на столбец свободных членов
1-ого
столбца на столбец свободных членов
❶❶ Величины, которые полностью определяются своим численным значением наз. скалярными(S,V,t,m,длина)
Однако встречаются и другие величины (скорость,сила,ускорения) определяются не только своим числовым значением, но и направлением – такие величины наз. - векторными
Векторная величина геометрически изображется с помощью вектора
Вектор – это направленный, прямолинейный отрезок т.е. отрезок, имеющий определенную длину и определенное направление
Если
А – начало вектора, а В – его конец, то
 обозначение вектора
обозначение вектора
Вектор наз. противоположным вектору
наз. противоположным вектору
Длиной или модулем вектора наз. Длина отрезка и обозначается | |
Вектор,
длина которого равна нулю наз.
нулевым
 (нулевой вектор не имеет направления)
(нулевой вектор не имеет направления)
Вектор,
длина которого равна 1 наз. единичным

Единичный
вектор, направление которого совпадает
с направлением
 наз. ортом
вектора
и обозначается
наз. ортом
вектора
и обозначается
Векторы
и
 наз. коллинеарными
если они лежат на одной прямой или на
параллельных (
||
)(
= λ
)
наз. коллинеарными
если они лежат на одной прямой или на
параллельных (
||
)(
= λ
)
Коллинеарные векторы могут быть направлены одинаково или противоположно
Нулевой вектор считается коллинеарным любому вектору
Два вектора и наз. равными ( = ) если они коллинеарные, одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку о пространства.
Три (и более) вектора наз. компланарными если они лежат в одной плоскости или в параллельных плоскостях
Совместим параллельным переносом начало неколлинеарных векторов а и в, начало и концы векторов образуют вершины Δ, угол между вектором и наз. Угол при вершине этого Δ, соответствующий началу векторов, если векторы сонаправлены, то угол между ними равен нулю, если противоположно направлены , то угол равен 180⁰
❶❷ Линейные операции над векторами
Под линейными операциями над векторами понимают операции + и – векторов, а также умножение вектора на число
Пусть заданы
и
два произвольных вектора, возьмем
произвольную т. О и построим вектор
 =
от точки А построим вектор
=
от точки А построим вектор
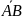 =
.
Вектор
=
.
Вектор
 наз. суммой
векторов
(начало 1 вектора и конец 2 вектора)
наз. суммой
векторов
(начало 1 вектора и конец 2 вектора)
Сумма 2-х векторов можно также построить по правилу параллелограмма
Под разностью векторов и понимается вектор
 =
-
=
-
= +
Конец 2-ого и конец 1-ого
Отметим, что в параллелограмме построенном на векторах и одна направленная диагональ является суммой + , а другая разностью
Можно вычитать векторы по правилу:
- = + (- )
Произведением вектора на скаляр (число) λ наз. вектор λ , который имеет длину |λ|*| |
Коллинеарен вектору , имеет направление вектора если λ>0 и противоположное направление если λ<0
Линейные операции и свойства векторов
+
 +
+
( и
 +
=
+(
+
)
+
=
+(
+
) (
( *
) = (
*
) = (
 )
)
(
 )
=
)
=
 +
+

λ( + ) =
 + λ
+ λ
❶❸ Системы координат на плоскости
Для определения положения точек на плоскости пользуются различными системами координат.
Под системой координат надо понимать условия, которые позволяют однозначно определить положение точки на плоскости или в пространстве при помощи чисел.
На плоскости чаще всего пользуются декартовой системой координат (ДСК) и полярная СК.
Каждая из них может быть косоугольной и прямоугольной
Декартовая СК
ДСК(прямоуг.) наз. совокупность двух пересекающихся под прямым углом осей координат, для которых указаны масштаб и направление.
Полярная СК
Пусть на плоскости задана точка О назовем ее полюсом, проходящую через нее ось – полярной осью (Ох), укажем единицу масштаба и будем определять положение произвольной точки М на плоскости по отношению к полюсу и полярной оси

М(Р;ϕ)


 х
х
ОМ
- полярный радиус, если
 <
0 то ОМ’ расположен на продолжении ОМ
<
0 то ОМ’ расположен на продолжении ОМ
Φ – полярный угол, измеряется в радианах
Угол в 1 радиан(57⁰)- центральный угол окружности, длина дуги которого равна R окружности
❶❹ Аналитическое представление вектора в ДСК
Если
обозн. вектор
и принять, то А( ;
; )
В(
)
В( ;
; ),
то координаты вектора
={
-
;
-
}
),
то координаты вектора
={
-
;
-
}
Координаты вектора получаются разностью координат его конца и начала
❶❺Действия над векторами
Пусть заданы вектора
( ;
; )
)
( )
произвольные векторы на плоскости,
тогда над ними можно производить
следующие действия:
)
произвольные векторы на плоскости,
тогда над ними можно производить
следующие действия:
1) = {
+
= {
+
 ;
+
;
+
 }
}
2) = {
-
;
-
}
= {
-
;
-
}
3)m = {m ; m }
4) = {
*
;
*
}
– скалярное произведение
= {
*
;
*
}
– скалярное произведение
Скалярным
произведением 2-х векторов
наз. такое число , которое равно
произведению длин этих векторов на
 угла между ними
угла между ними
 =
=
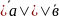 |*cos
ϕ
|*cos
ϕ
В екторное
произведение 2-х векторов явл. Такой
3-й вектор, который численно равен S
параллелограмма, построенного на данных
векторах и направлен перпендикулярно
плоскости этих векторов
екторное
произведение 2-х векторов явл. Такой
3-й вектор, который численно равен S
параллелограмма, построенного на данных
векторах и направлен перпендикулярно
плоскости этих векторов
в
а



Нормирование вектора
Пусть направляющий вектор( 0 ) – единичный вектор ( ; )
Тогда
 * |
* | ; |
|=
1
; |
|=
1
=

Длина вектора
|
=
 (пространство)
(пространство)
|
=
 (плоскость)
(плоскость)
Если
вектор
=
задан координатами, то А( )
В(
)
В(
|
= {
❷⓿Различные виды уравнения прямой
Каждая
прямая на плоскости
 определяется линейным уравнением 1-й
степени с 2-мя неизвестными, обратно
каждое линейное уравнение 1-ого порядка
с 2-мя неизвестными определяет некоторую
прямую на плоскости
определяется линейным уравнением 1-й
степени с 2-мя неизвестными, обратно
каждое линейное уравнение 1-ого порядка
с 2-мя неизвестными определяет некоторую
прямую на плоскости
1) Ах + Ву + С = О общее уравнение прямой, где А,В,С – постоянные коэффициенты, причем А и В одновременно не обращаются в 0

Н ормальный
вектор прямой(
ормальный
вектор прямой(
 = (А;В))
˩ прямой
= (А;В))
˩ прямой
Частные случаи уравнения:
 С = 0 – проходит
через начало координат
С = 0 – проходит
через начало координат
 = 0 - уравнение
будет || оси
= 0 - уравнение
будет || оси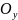
 0
0
 - уравнение || оси
- уравнение || оси
В и С = 0 – совпадает с
 - совпадает с
- совпадает с
2) Уравнение прямой с угловым коэффициентом
у = kх + в, где k = tgɑ
k
– угловой коэф. прямой , tgɑ
- угол, который прямая образует с положит.
направлением
 в - ордината точки пересечения с
в - ордината точки пересечения с
(||)

(˩)


3 )Уравнение прямой, проходящей через данную точку в данном направлении
К(х - )
=
)
=

К= tgɑ
 ;
; - координ. точки, которая задана
- координ. точки, которая задана
4)Уравнение прямой, проходящей через 2 данные точки


 К,
проходящий через 2 данные точки
определяется
К,
проходящий через 2 данные точки
определяется
К=
❷❹ Множество – совокупность, семейство, собрание, группа, набор.
К одному множеству обычно относят объекты, обладающие некоторыми одинаковыми признаками.
Объекты, составляющие множество наз. элементами множества.
Если множество А состоит из х,у,…z, то
А=
Множество А и В наз. равными ( совпадающими) , если каждый элемент множества А явл. элементом множества В и каждый элемент В является элементом А.
Принадлежность элемента Х множеству А обозначается:
Х ͼ А; у ͼ А
ͼ А; у ͼ А
Основатель теории множеств немецкий математик Георг Кантор: « Множество есть многое мыслимое нами как единое»
Множество, содержащее конечное число элементов называется конечным множеством.
Множество, содержащее бесконечное число элементов называется бесконечным множеством.
Множество,
содержащее n
элементов
называется
 –элементным
множеством.
–элементным
множеством.
Множество не содержит повторяющихся элементов и порядок их записи в списке не имеет значения.
 В
математике рассматривают также
множество, которое не содержит ни одного
элемента, такие множества называются
пустыми. (
o )
В
математике рассматривают также
множество, которое не содержит ни одного
элемента, такие множества называются
пустыми. (
o )
Необходимость введения пустого множества обуславливается тем, что иногда заранее неизвестно существуют ли элементы, удовлетворяющие данному характеристическому св-ву
Подмножество возникает всякий раз, когда некоторое множество рассматривают как часть другого множества или выделяют в некотором множестве другое множество
Если любой элемент множества В принадлежит множеству А, то множество В наз. подмножеством множества А ; В ϲ А; А Ɔ В
Часто элементы множеств упорядочивают по какому-либо признаку, которым они обладают
Упорядоченное множество – это такое множество, элементы которого занумерованы определенным образом
Множество двухзначных четных положительных чисел не превосход. 20
А = {10,12,14,16,18,20}
Рассмотрим конечную упорядоченную последовательность элементов из некоторого заданного множества А символом Аn, которую назовем кортежем
Кортеж – это конечная упорядоченная последовательность элементов какого-либо множества, которая допускает повторение элементов
Если А - множество цифр, то кортеж – это будет конечная последовательность чисел.
Число элементов кортежа наз. длиной кортежа
Кортеж, не содержащий ни одного компонента (длина равна 0) наз. пустым кортежем и обозначается <>
2
картежа ɑ =
< >
>
ɣ
=<
 >
наз. равными,
если они имеют одинаковую длину, причем
их компоненты, имеющие одинаковый
номер, то n=m,
>
наз. равными,
если они имеют одинаковую длину, причем
их компоненты, имеющие одинаковый
номер, то n=m,

Отличия понятия кортеж от понятия множества:
1) в кортеже компоненты могут повторятся, в множестве все элементы различны
2) в множестве порядок элементов не имеет значение, а в картеже имеет
3) в упорядоченном множестве в отличие от кортежа элементы также не повторяются
❷❺ Операции над множествами
Объединением или суммой множеств А и В наз. множество С, состоящее из элементов, каждый из которых принадлежит или множеству А или В
С = АUВ
Законы для объединения множеств:
Если А U В = В U А
А U (В U С) = (А U В) U С
Пересечением множеств А и В наз. множество С, состоящее из всех элементов, каждый из которых принадлежит и множеству А и множеству В:
С = А∩В
Законы пересечения множеств:
А∩В = В∩А
А∩ (В∩С) = (А∩В)∩С
Разностью множеств А и В наз. множество С, состоящее из всех элементов множества А , которые принадлежат множеству В
С = А \ В
❷❻ Комбинаторика – область математики, в которой изучается вопрос о том сколько различных конфигураций, удовлетворяющих тем или иным условиям можно составить из заданных объектов
Перебор всех возможных вариантов или хотя бы подсчитывать их число – комбинаторн
С комбинаторными вычислениями приходится иметь место представителям многих специальностей: администраторы, диспетчера.
Правила комбинаторного сложения
Иногда удается разбить все изучаемые случаи на несколько групп, причем каждая искомая комбинация входит в одну группу. В этом случае общее число комбинации равно сумме чисел комбинации во всех группах(правило суммы)
 Если
элемент а
можно выбрать из множества А
n(A)
способами, а элемент в
из множества В
n(B)
способами, причем множества А
и В (A∩B
= O
) не имеют общих элементов , то выбор
или элемента а или элемента в можно
сделать способами , где n(АUВ)
= n(А)
+n(В)
Если
элемент а
можно выбрать из множества А
n(A)
способами, а элемент в
из множества В
n(B)
способами, причем множества А
и В (A∩B
= O
) не имеют общих элементов , то выбор
или элемента а или элемента в можно
сделать способами , где n(АUВ)
= n(А)
+n(В)
Немного сложнее обстоит дело, когда множества А и В имеют общие элементы, т.е. пересечение множеств А и В не пусто.
Поэтому правило сложения для пересекающихся множеств можно записать следующим образом:
Если элемент а из множества А можно выбрать n(А) способами, а элемент в из множества В n(B) способами, причем множества А и В имеют n(А∩В) общих элементов, то выбор или элемента а или элемента в можно сделать n(АUВ) = n(А) +n(В)- n(А∩В)
Правило сложения можно записать и для 3 пересек. Множеств
n(АUВUС)=n(А)+n(В)+n(С)-n(А∩В)-n(А∩С)-n(В∩С)-n(А∩В∩С)
Правила комбинаторного умножения
Часто при составлении комбинаций из двух элементов известно сколькими способами можно выбрать первый элемент, а затем сколькими способами второй, причем выбор первого элемента не влияет на число способов выбора второго. Сколькими способами можно выбрать пару, состоящую из первого и второго элементов
Правило:
Если элемент а можно выбрать из множества А n(A) способами и если после каждого такого выбора элемент в можно выбрать из множества В n(B) способами, то выбор пары (а,в) в указанном порядке можно выбрать n(A) * n(B) способами
Правило произведения можно применять при составлении комбинаций не только двух, но и большего числа элементов:
Пусть
требуется последовательно выбрать
k
элементов, причем выбор любого элемента
не влияет на число выборов последующих.
Если выбор первого элемента можно
произвести
 способами, второго
способами, второго
 способами…до k
– го элемента, то выбор k
– го
способами…до k
– го элемента, то выбор k
– го
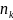 способами, то выбрать все k
элементов можно
способами, то выбрать все k
элементов можно

❷❼,❷❽
1)Перестановки Рn
В множестве из n- элементов
Свойство 1
Поскольку выбор первого элемента в перестановке не повлияет на числа возможностей выбора второго, выбор второго элемента не повлияет на число возможностей третьего, здесь можем воспользоваться правилом произведения
Произведение первых n-натуральных чисел n(n-1) (n-2)(n-3)*…*1*2*3 называется n- факториал и обозначается n! (5!=1*2*3*4*5)
Свойство 2
Рассмотрим задачу :
Сколькими
способами из n
различных предметов можно выбрать m
различных предметов и расположить их
в m
различных местах. Такое расположение
наз. размещением
из n
по m
и обозначается

=
Отметим, что если все k-групп одинаковы, т.е. каждая состоит из одних и тех же различных между собой n-элементов , то получаем число размещений с повторениями

Свойство 3

Рассмотрим задачу:
Какими
способами можно из множества , содержащего
n-элементов
выбрать подмножество, содержащее
m-элементов,
такое подмножество наз. сочетанием
из n
по m
и обозначается

❷❾ Изучением случайных явлений и процессов занимается теория вероятности.
Под испытанием понимают наблюдение, опыт, эксперимент
Случайным событием наз. такой исход испытания, который при соблюдении условий испытания может произойти, а может и не произойти
Для краткости их наз. событием
Достоверным событием наз. событие, которое при соблюдении условий испытания обязательно произойдет.
Невозможным событием наз. событие, которое заведомо не может произойти при соблюдении условий испытания
События наз. несовместимыми, если они взаимно исключают друг друга, т.е. никакие из них не могут появиться вместе, в противном случае события наз. совместимыми
2)Вероятность события. Основные свойства вероятности.
Испытания характеризуются не только своими возможными исходами и количеством, но и степенью их появления.
Степень возможности того, что случайное событие произойдет определяет специальная математическая характеристика, которая наз. вероятностью (Вероятность события А обозначается Р(А))
О вероятности может говорить:
1)только в связи с появлением того или иного события
2)вероятность событий можно сравнивать между собой
3)вероятность всякого события не может быть больше вероятности достоверного события
Пусть m(А) – это число элементарных событий, благоприятствующих наступлению события А в результате испытания
n(E) – общее число равновозможных элементарных событий, которые могут произойти в результате испытания, тогда вероятностью события А наз. отношение
❸⓿ - классическое
определение вероятности
- классическое
определение вероятности
Элементарные события должны быть равновозможными, т.е. условия испытания обеспечивают одинаковую возможность появления каждого из них. В противном случае вероятность события нельзя будет определить по формуле
Свойства вероятности:
1)Вероятность достоверного события равна 1
2)вероятность невозможного события равна 0
3)вероятность случайного события А есть положительное число, заключенное между 0 и 1 0≤Р(А)≤1
3)Вероятность объединения событий и правило сложения вероятностей
Событие, которое происходит т.и т. т. к. происходит хотя бы одно из событий А или В наз. объединением событий А и В, поэтому высказывание «произошло событие АUВ» обозначает, что произошло событе А или произошло событие В или произошли оба события
