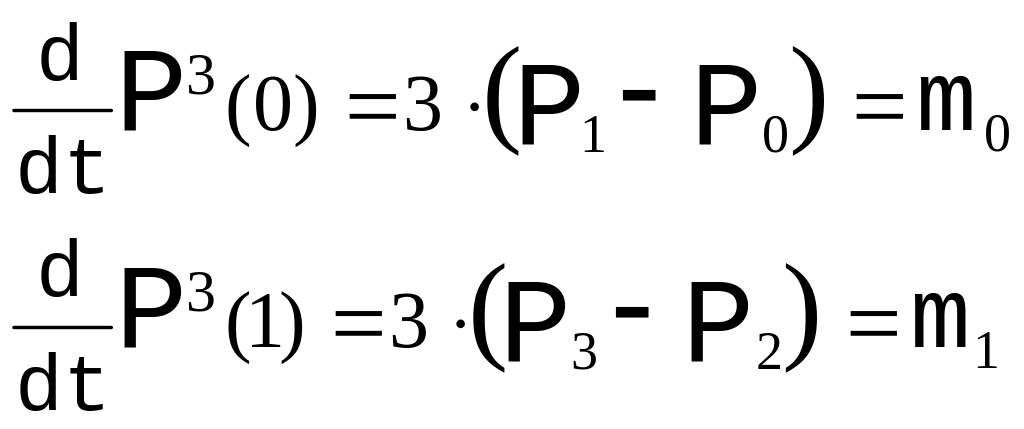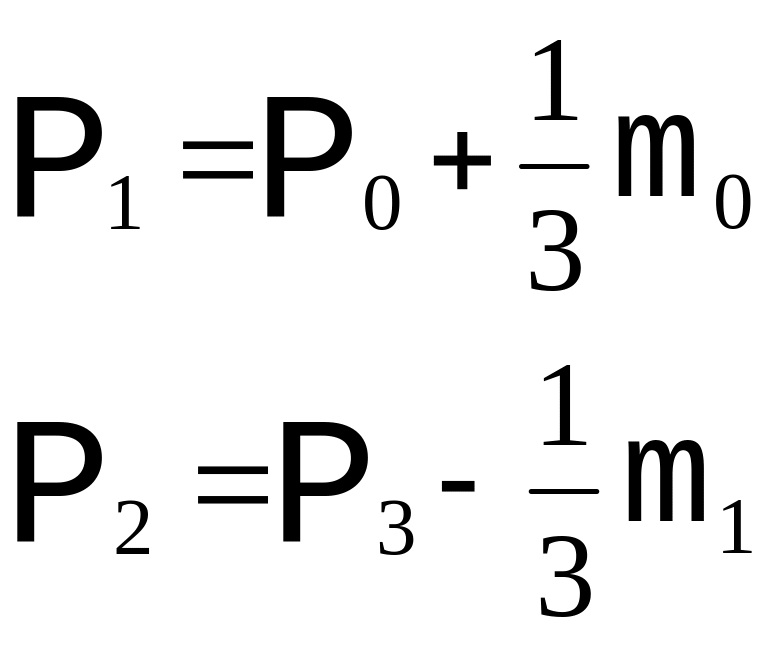Свойства кривых Безье
1) Инвариантность относительно аффинных преобразований;
2) Инвариантность относительно линейных замен параметризации;
Кривая Безье принадлежит выпуклой оболочке опорных точек (следует из геометрического способа построения);
Следствие: Если все опорные точки лежат на одной прямой, то кривая Безье вырождается в отрезок, соединяющий эти точки.
4) Кривая Безье проходит через
и
![]() ;
;
5) Симметричность: если рассматривать контрольные точки в противоположном порядке, то кривая не измениться;
6) Степень многочлена, представляющего кривую в аналитическом виде на 1 меньше числа опорных точек;
7) Векторы касательных в точках
и
коллинеарны
![]() и
и
![]() ,соответственно.
,соответственно.
Замечание:
Хотя все выкладки проводились в
![]() ,
аналогичные построения и свойства
справедливы и в
,
аналогичные построения и свойства
справедливы и в
![]() .
.
Визуализация кривых Безье
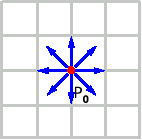
1) Прямой метод
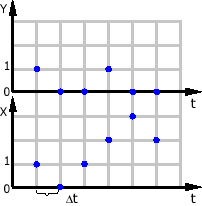
Рис. 8. Построение кривых Безье прямым методом.
|
Подберем шаг dt так, чтобы dx и dy были <1 (т.е. мы не пропустим ни одного пиксела).
Алгоритм: t=0; while(t≤1) { x=x(t); y=y(t); plot(x,y); t+=dt; }
Недостаток: при малых смещениях по x и y много итераций проходит зря. |
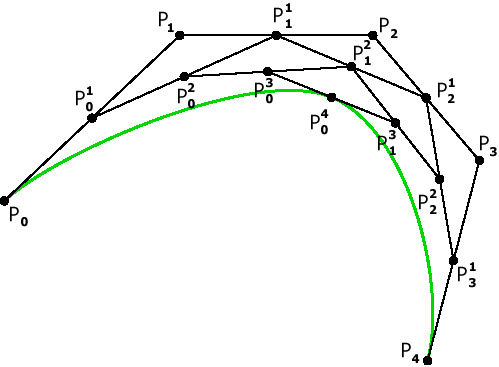
Метод разбиения (subdivision)
Рис. 9. Построение кривой Безье методом разбиения.
|
Предложен de Casteljau.
Если
рассмотреть участок между
|
Алгоритм:
PutPixel(![]() );
);
PutPixel( );
DrawCurve
(![]() )
)
{
// Проверка на завершение
if ( BBox( ) < pixelsize ) return;
if ( - прямая линия с точностью до пиксела )
{
Нарисовать эту линию;
return;
}
Найти
![]() ;
;
PutPixel(![]() );
);
// Нарисовать половинки
DrawCurve(![]() );
);
DrawCurve(![]() );
);
}
2) Сплайны, составленные из кривых Безье
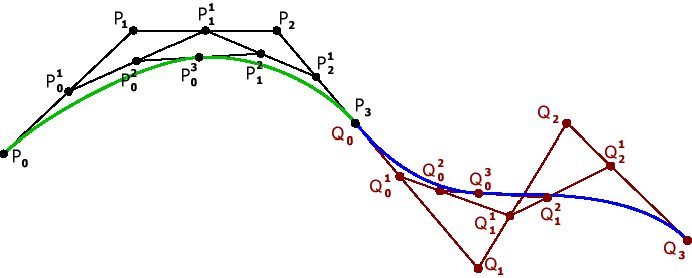
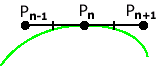
Рис. 10. Состыкованные кубические кривые Безье.
Д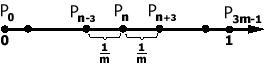 ля
упрощения будем считать, что параметризация
равномерная, т.е. длины отрезков, которые
пробегает параметр на каждом из участков,
равны.
ля
упрощения будем считать, что параметризация
равномерная, т.е. длины отрезков, которые
пробегает параметр на каждом из участков,
равны.
Для того чтобы рассмотреть условия на и , необходимо найти производные кривых Безье:
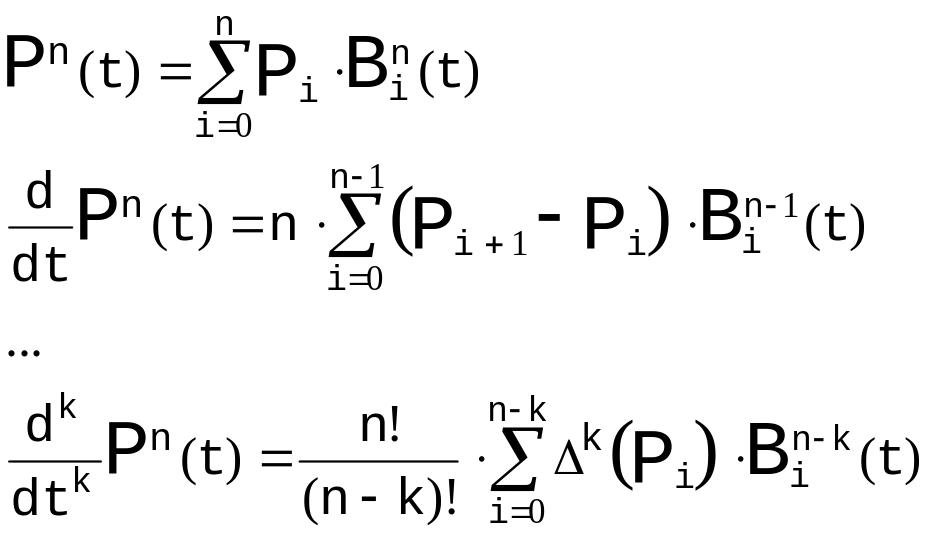 ,
где
,
где
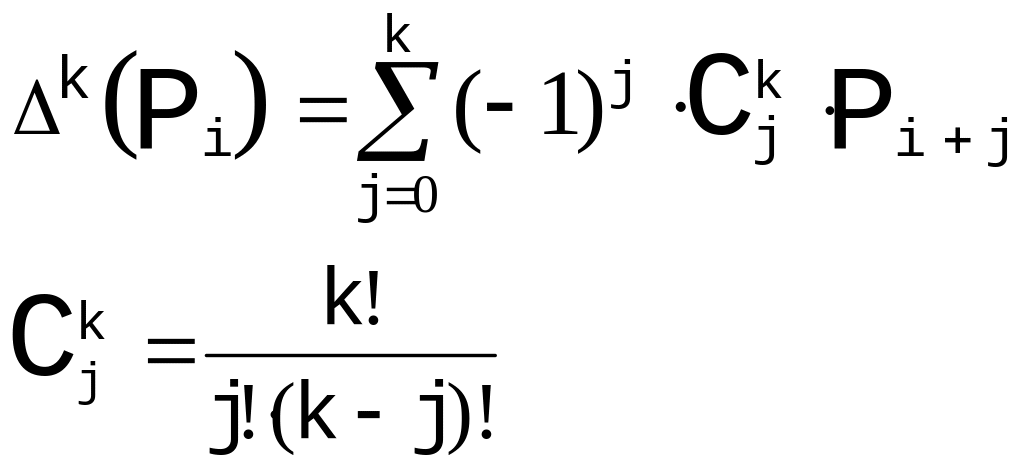
Ограничимся в рассмотрении кубическими кривыми Безье, которые более всего распространены.
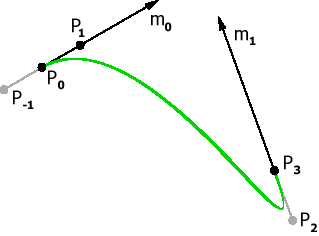
1) Требование
Рис. 11. Стыковка с требованием |
Пусть заданы значение производных на концах: m0 и m1 :
Таким образом, для того, чтобы в точках стыковки производные были равны необходимо, чтобы
|
2) Требование
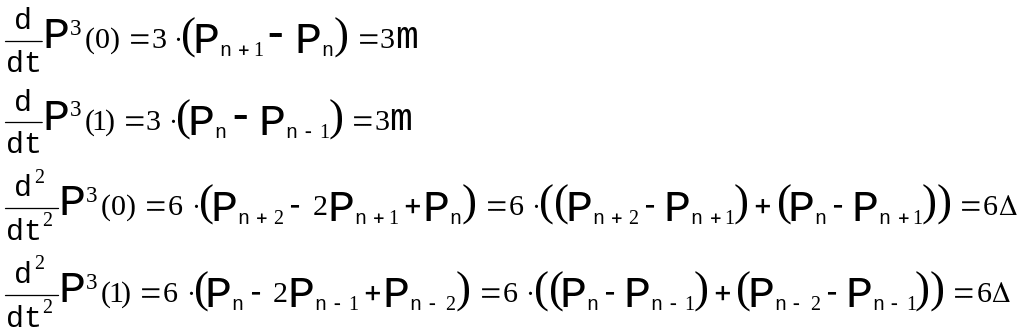
Рис. 12. Стыковка с требованием . |
Из требования
в точках стыковки получаем
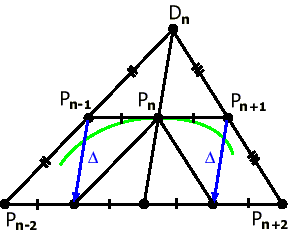
Распространяя эти
рассуждения на все точки стыковки,
получаем, что для задания формы такого
сплайна достаточно задать точки
|
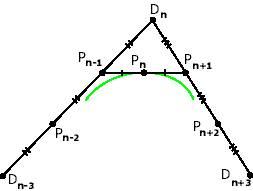
Рис. 13. Связь между точками для соседних сегментов. |
Замечание: Для замкнутой кривой задание краевых точек не нужно.
|