
- •Решить задачу «Производство-потребление»:
- •Аналитическая геометрия на плоскости
- •Векторная алгебра и аналитическая геометрия в пространстве
- •Квадратичные формы.
- •1.2 Типовые аттестационные работы
- •1.3. Вопросы к экзамену
- •1.4 Типовой экзаменационный билет по дисциплине «Линейная алгебра»
- •Технологии и формы преподавания и обучения
Квадратичные формы.
а)Привести квадратичную форму F(x,y,z), к каноническому виду;
б)определить знакоопределенность квадратичной формы.
Вариант 1.
F(x, y, z) = 4x2 + 6y2+4z2 + 4xz – 8y–4z + 3
Вариант 2.
F(x, y, z) = x2 + 5y2+z2 + 2xy + 6xz +2yz–2x + 6y–10z
Вариант 3.
F(x, y, z) = x2 + y2–3z2 – 2xy – 6xz–6yz + 2x + 2y + 4z
Вариант 4.
F(x, y, z) = x2 – 2y2+z2 + 4xy – 8xz – 4yz–14x – 4y + 14z + 16
Вариант 5.
F(x, y, z) = 2x2 + y2+2z2 – 2xy – 2xz + x–4y – 3z + 2
Вариант 6.
F(x, y, z) = x2 – 2y2+z2 + 4xy – 10xz+4yz + x + y – z
Вариант 7.
F(x, y, z) = 2x2 + y2+2z2 – 2xy – 2xz+4x – 2y
Вариант 8.
F(x, y, z) = x2 + y2–4z2 + 2xy + 4xz+4yz – 6z + 1
Вариант 9.
F(x, y, z) = 4xy+2x + 4y – 6z – 3
Вариант 10.
F(x, y, z) = xy + xz+ yz+ 2x + 2y – 2z
Вариант 11.
F(x, y, z) = 4x2 + 6y2+4z2 + 4xz – 8y–4z + 3
Вариант 12.
F(x, y, z) = x2 + 5y2+z2 + 2xy + 6xz +2yz–2x + 6y–10z
Вариант 13.
F(x, y, z) = x2 + y2–3z2 – 2xy – 6xz–6yz + 2x + 2y + 4z
Вариант 14.
F(x, y, z) = x2 – 2y2+z2 + 4xy – 8xz – 4yz–14x – 4y + 14z + 16
Вариант 15.
F(x, y, z) = 2x2 + y2+2z2 – 2xy – 2xz + x–4y – 3z + 2
Вариант 16.
F(x, y, z) = x2 – 2y2+z2 + 4xy – 10xz+4yz + x + y – z
Вариант 17.
F(x, y, z) = 2x2 + y2+2z2 – 2xy – 2xz+4x – 2y
Вариант 18.
F(x, y, z) = x2 + y2–4z2 + 2xy + 4xz+4yz – 6z + 1
Вариант 19.
F(x, y, z) = 4xy+2x + 4y – 6z – 3
Вариант 20.
F(x, y, z) = xy + xz+ yz+ 2x + 2y – 2z
1.2 Типовые аттестационные работы
Типовая аттестационная работа №1
Координатная, матричная и векторная формы записи СЛАУ. Дайте определение решения СЛАУ. Общее и частное решения СЛАУ.
Найти ранг матрицы при различных значениях параметра
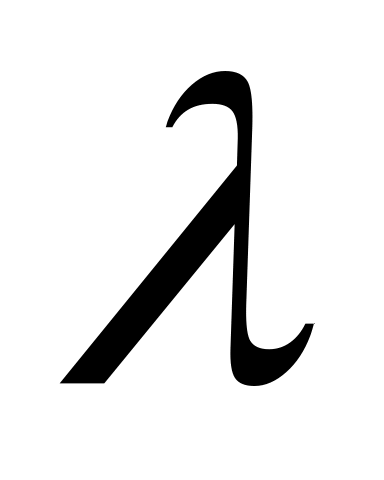 :
:
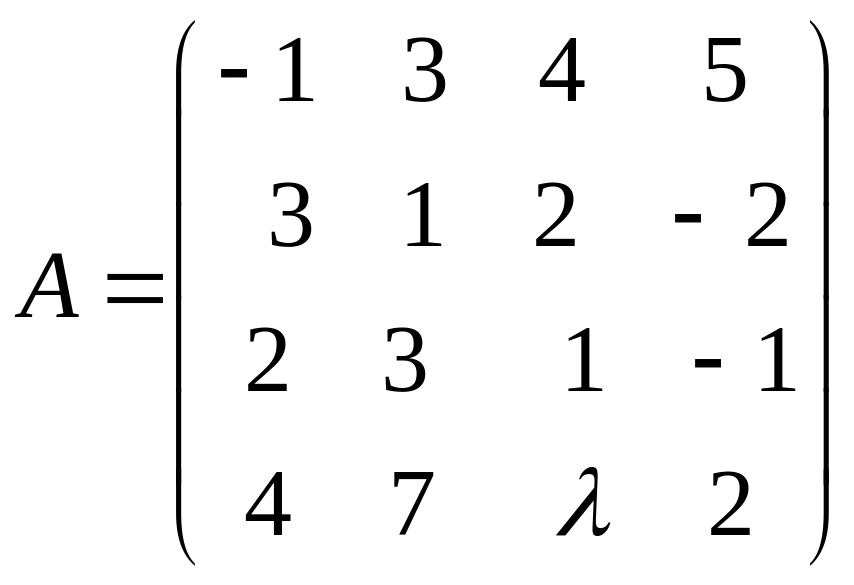
3. Решить матричное уравнение:
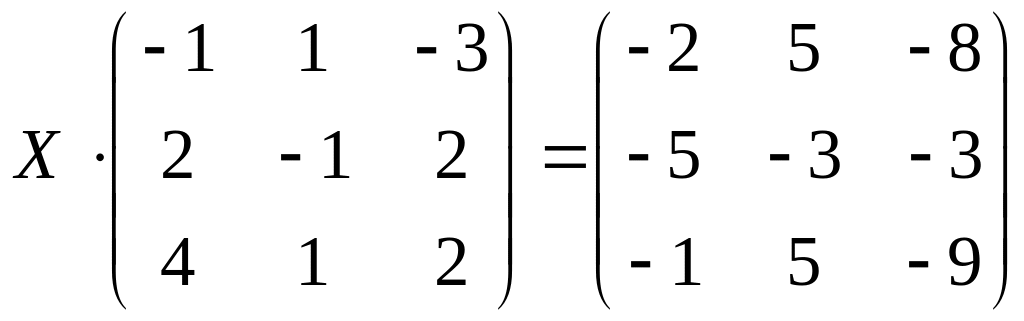
4. Исследовать и найти решение (если оно существует) системы линейных уравнений:

Типовая аттестационная работа №2
Векторное и смешанное произведение векторов.
Выяснить являются ли векторы a=(2,-1,3), b(1,4,-1), c(0,-9,5) линейно зависимыми.
Векторы e1, e2, e3 и х заданы своими координатами в некотором базисе. Показать, что векторы e1, e2, e3 сами образуют базис и найти координаты вектора х в этом базисе.
Найти собственные значения и собственные векторы матрицы А =
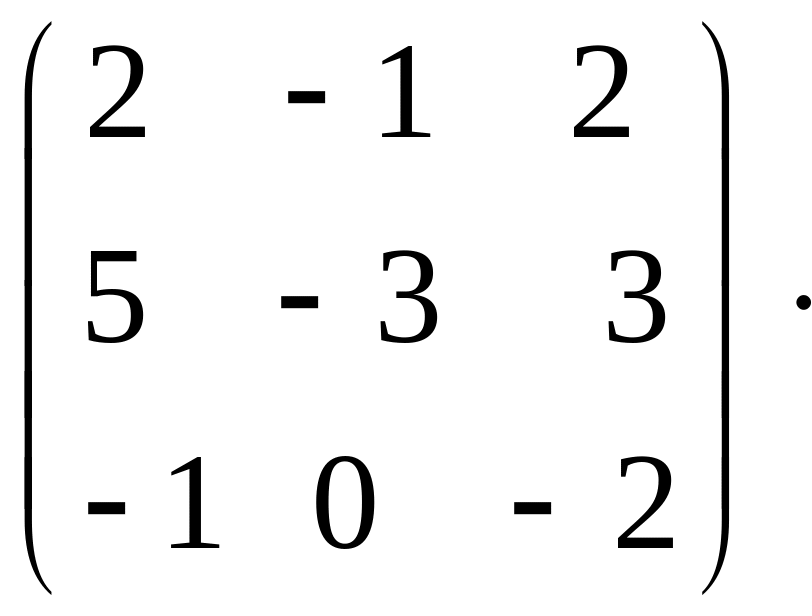
Типовая аттестационная работа №3
1.Определить тип кривой по заданному уравнению, привести к каноническому виду и построить кривую, найти координаты фокусов. Для эллипса и гиперболы определить эксцентриситет, составить уравнения асимптот для гиперболы; для параболы найти значение параметра, составить уравнения директрисы:
![]()
2.Написать уравнение плоскости, проходящей через точку М(2,-4,3), перпендикулярно ее радиусу вектору ОМ
1.3. Вопросы к экзамену
Матрицы, их классификация, сложение матриц и умножение матрицы на число, умножение матрицы на матрицу, транспонирование матрицы, свойства операций над матрицами.
Элементарные преобразования матриц и матрицы элементарных преобразований, теорема о приведении произвольной матрицы к верхней трапециевидной форме.
Определитель и след квадратной матрицы, свойства определителей.
Ортогональная матрица, теорема об определителе ортогональной матрицы.
Линейные операции над геометрическими векторами и их свойства.
Линейное пространство, подпространство линейного пространства, линейное многообразие, линейная оболочка, сумма и пересечение подпространств, изоморфизм линейных пространств.
Линейная зависимость векторов и ее геометрический смысл.
Базис и размерность линейного пространства, координаты вектора.
Ранг матрицы, теорема о базисном миноре, инвариантность ранга матрицы относительно ее элементарных преобразований.
Аффинная и прямоугольная декартова системы координат.
Проекции геометрического вектора на плоскости и в пространстве.
Скалярное, векторное и смешанное произведения геометрических векторов.
Преобразование аффинной и прямоугольной декартовой системы координат.
Преобразование координат вектора при переходе к новому базису.
Системы линейных уравнений: основные определения, каноническая форма записи системы линейных алгебраических уравнений.
Система линейных уравнений с квадратной невырожденной матрицей, правило Крамера.
Элементарные преобразования системы линейных алгебраических уравнений.
Исследование и решение системы линейных алгебраических уравнений методом последовательного исключения неизвестных Жордана — Гаусса.
Геометрические свойства решений системы линейных уравнений.
Поиск базисных решений, общего решения и фундаментального решений системы линейных алгебраических уравнений.
Обратная матрица: определение, свойства, условие существования.
Обращение матрицы методом Жордана.
Прямая, различные виды уравнений прямой на плоскости и плоскости в пространстве.
Взаимное расположение прямых на плоскости и плоскостей в пространстве, Прямая на плоскости и плоскость в пространстве в прямоугольной декартовой системе координат.
Прямая в пространстве, взаимное расположение прямых в пространстве.
Комплексные числа и операции над ними.
Многочлены, деление многочленов, корни многочлена, теорема Безу.
Эллипс, гипербола, парабола, их канонические уравнения и свойства.
Общее уравнение линии второго порядка на плоскости, характеристический многочлен, метод вращений.
Классификация линий второго порядка на плоскости, каноническое уравнение, метод Лагранжа.
Евклидовы пространства, длина вектора и ее свойства.
Ортогональные векторы, ортогональный и ортонормированный базис линейного пространства, процесс ортогонализации.
Линейный оператор и его матрица, свойства линейного оператора.
Произведение линейных операторов, образ и ядро линейного оператора, обратный оператор.
Собственные значения и собственные векторы матрицы.
Собственные значения и собственные векторы линейного оператора.
Приведение квадратичной формы к каноническому виду методом Лагранжа.
Критерий Сильвестра положительной определенности квадратичной формы.
