1.     Математическая модель. Ее основные элементы

Математи́ческая моде́ль — это математическое представление реальности^[1].

Математическое моделирование — это процесс построения и изучения математических моделей.

Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его математической моделью и затем изучают последнюю.

 Моделирование — это опосредованное практическое или теоретическое исследование объекта, при котором непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель):

1. находящаяся в некотором объективном соответствии с познаваемым объектом;

2. способная замещать его в определенных отношениях;

3. дающая при её исследовании, в конечном счете, информацию о самом моделируемом объекте.^[2]

По учебнику Советова и Яковлева ^[3]: «модель (лат. modulus — мера) — это объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала». (с. 6) «Замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели называется моделированием». (с. 6) «Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи».

По Самарскому и Михайлову ^[4], математическая модель — это «„эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям, и т. д.» Существует в триадах «модель-алгоритм-программа». «Создав триаду „модель-алгоритм-программа“, исследователь получает в руки универсальный, гибкий и недорогой инструмент, который вначале отлаживается, тестируется в пробных вычислительных экспериментах. После того как адекватность (достаточное соответствие) триады исходному объекту установлена, с моделью проводятся разнообразные и подробные „опыты“, дающие все требуемые качественные и количественные свойства и характеристики объекта». (с.7-8)

По монографии Мышкиса ^[5]: «Перейдем к общему определению. Пусть мы собираемся исследовать некоторую совокупность   свойств реального объекта   с помощью математики (здесь термин объект понимается в наиболее широком смысле: объектом может служить не только то, что обычно именуется этим словом, но и любая ситуация, явление, процесс и т. д.). Для этого мы выбираем (как говорят, строим) „математический объект“   — систему уравнений, или арифметических соотношений, или геометрических фигур, или комбинацию того и другого и т. д.,— исследование которого средствами математики и должно ответить на поставленные вопросы о свойствах  . В этих условиях   называется математической моделью объекта   относительно совокупности   его свойств». (с.8)

По Севостьянову А. Г.^[6] : «Математической моделью называется совокупность математических соотношений, уравнений, неравенств и т.п., описывающих основные закономерности, присущие изучаемому процессу, объекту или системе».

2.     Основные типы моделей

Математические модели, используемые в экономике, можно подразделять на классы по ряду признаков, относящихся к особенностям моделируемого объекта, цели моделирования и используемого инструментария: модели макро- и микроэкономические, теоретические и прикладные, оптимизационные и равновесные, статические и динамические. Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупненные материальные и финансовые показатели: ВНП, потребление, инвестиции, занятость, процентную ставку, количество денег и другие. Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики, либо поведение отдельной такой составляющей в рыночной среде. Вследствие разнообразия типов экономических элементов и форм их взаимодействия на рынке микроэкономическое моделирование занимает основную часть экономико-математической теории. Наиболее серьезные теоретические результаты в микроэкономическом моделировании в последние годы получены в исследовании стратегического поведения фирм в условиях олигополии с использованием аппарата теории игр. Теоретические модели позволяют изучать общие свойства экономики и ее характерных элементов дедукцией выводов из формальных предпосылок. Прикладные модели дают возможность оценить параметры функционирования конкретного экономического объекта и сформулировать рекомендации для принятия практических решений. К прикладным относятся прежде всего эконометрические модели, оперирующие числовыми значениями экономических переменных и позволяющие статистически значимо оценивать их на основе имеющихся наблюдений. В моделировании рыночной экономики особое место занимают равновесные модели. Они описывают такие состояния экономики, когда результирующая всех сил, стремящихся вывести ее из данного состояния, равна нулю. В нерыночной экономике неравновесие по одним параметрам (например, дефицит) компенсируется другими факторами (черный рынок, очереди и т.п.). Равновесные модели дескриптивны, описательны. В нашей стране долгое время преобладал нормативный подход в моделировании, основанный на оптимизации. Оптимизация в теории рыночной экономики присутствует в основном на микроуровне (максимизация полезности потребителем или прибыли фирмой); на макроуровне результатом рационального выбора поведения экономическими субъектами оказывается некоторое состояние равновесия. В моделях статических описывается состояние экономического объекта в конкретный момент или период времени;динамические модели включают взаимосвязи переменных во времени. В статических моделях, обычно зафиксированы значения ряда величин, являющихся переменными в динамике, — например, капитальных ресурсов, цен и т.п. Динамическая модель не сводится к простой сумме ряда статических, а описывает силы и взаимодействия в экономике, определяющие ход ' процессов в ней. Динамические модели обычно используют аппарат дифференциальных и разностных уравнений, вариационного исчисления. Детерминированные модели предполагают жесткие функциональные связи между переменными моделями.Стохастические модели допускают наличие случайных воздействий на исследуемые показатели и используют инструментарий теории вероятностей и математической статистики для их описания.

3.     Функциональная зависимость.

    Функциональная зависимость - это такая связь математических (не случайных) переменных, при которой в любой моментвремени каждое единственное значение одной переменной связано только с одним единственным значением другой.       В живых системах и социальных системах реально такой связи нет, так как переменные всех живых систем, адекватные ихвероятностной сущности - случайные переменные. Функциональная зависимость - это абстракция, сильно упрощенная модельреальности. Необоснованное использование функциональной зависимости в познании может вести к утрате значительной части информации об изучаемом объекте, неэффективному исследованию. Вместе с тем, при наличии достаточных оснований для выбора функциональной зависимости, она может быть полезным инструментом познания.

4.     Построение и анализ графиков функций

Построение графиков и исследование функций - важные темы математического анализа. Чтобы выполнить построение, нужно сначала исследовать функцию. А чтобы исследовать, нужно знать алгоритм, уметь находить область определения, производную первого и второго порядка, односторонние пределы, асимптоты и так далее. Рассмотрим алгоритм полного исследования функции.

Исследование функций

1. Находим область определения.

Например, y=lnx определена для x>0, y=x для x≥0, y=1x для x≠0, y=ex для x∈ℝ, ℝ - множество действительных чисел, (-∞,+∞), от минус бесконечности до плюс бесконечности.

2. Находим точки пересечения с осями координат.

x=0, y = ? y=0, x = ?

3. Находим точки разрыва, исследуем на непрерывность.

Например, для y=1x x = 0 - точка разрыва, y=ex непрерывна на всей числовой оси.

4. Исследуем на чётность и нечетность.

Например, y=1x - нечётная, так как y(-x) = -1x = -y(x).

5. Исследуем на периодичность.

Например, для y=cosx период равен T=2π.

6. Находим асимптоты.  Вертикальные асимптоты находятся с помощью односторонних пределов в точках разрыва из пункта 3, горизонтальные и наклонные асимптоты находятся по формулам: y=kx+b, k=limx→∞yx, b=limx→∞(y-kx).

7. Исследуем на монотонность, находим интервалы возрастания и убывания, находим первую производную.

8. Находим вторую производную, точки перегиба и интервалы выпуклости, вогнутости.

9. Строим график.

Построение графиков

Построение можно выполнить на основе проведенного анализа, можно с помощью программы для построения графиков, скачать и использовать которую можно бесплатно.

Вы можете нам отправить задание по дифференциальному исчислению или заказать решение контрольной работы по математическому анализу.

Рассмотрим пример для y=1-x33.

D(y)=ℝ. Общего вида, т.е. ни чётная, ни нечётная. x=0→y=1;y=0→x=1⇒A(0,1),B(1,0) - точки пересечения с осями координат. k=limx→∞1-x33x = limx→∞1x3-13=-1,  b = limx→∞(1-x33+x) = limx→∞(1-x33+x)((1-x3)23+x2-x1-x33)(1-x3)23+x2-x1-x33= limx→∞1-x3+x3(1-x3)23+x2-x1-x33 = limx→∞1(1-x3)23+x2-x1-x33=0. y=kx+b⇒y=-x - наклонная асимптота. y' = 13(1-x3)-23·(-3x2) = -x2(1-x3)-23<0⇒функция убывает на ℝ, экстремумов нет. y'' = -2x(1-x3)-23+x2·23(1-x3)-53·(-3x2) = -2x(1-x3)-23-2x4(1-x3)-53 = -2x(1-x3)53 y''=0⇒x=0,x≠1.

Вогнута на (-∞,0)∪(1,+∞), выпукла на (0,1). x=0,x=1 - точки перегиба.

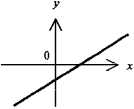
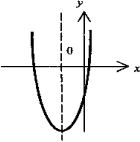
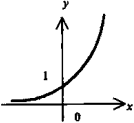
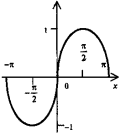
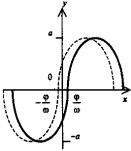
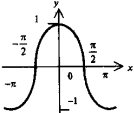
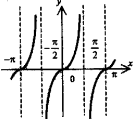
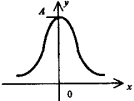
5.     Элементарные функции и их графики

рафики элементарных функций

Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность) Парабола - график функции квадратного трёхчлена у = ах2 + bх + с. Имеет вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 - максимум. Точки пересечения (если они есть) с осью абсцисс - корни соответствующего квадратного уравнения ax2 + bx +с =0 Гипербола - график функции  . При а > О расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0). Экспонента (показательная функция по основанию е) у = еx. (Другое написание у = ехр(х)). Асимптота - ось абсцисс. Логарифмическая функция y = logax (a > 0) у = sinx. Синусоида - периодическая функция с периодом Т = 2π у = а•sin(ωx+φ) - функция гармонических колебаний. Обозначения: а - амплитуда, ω - частота (ω = 2π/Т), φ - фаза (сдвиг). Косинусоида у = cosx (графики у = sinx и у = cosx сдвинуты по оси х на  ) Тангенсоида y = tgx. Точки разрыва при х =  (2k -1), где k = 0, ±1, ±2,.. Вертикальные асимптоты в этих точках. Гауссиана у = Аe-(ax2). Кривая "нормального" закона распределения ошибок, у которого ,  , σ 2 - дисперсия ошибки. Симметрия относительно оси у. у = secx - кривая "цепной линии", эту форму принимает абсолютно гибкая нить, подвешенная в параллельном поле тяжести. А полная функция периодична, и её асимптоты х =  (2k -1), как у функции y = tgx. Круг с центром в точке (xo, yo) радиуса r. (x-xo)2 + (y-yo)2 = r2 Эллипсс центром в точке (xo, yo). Большая полуось а, малая b, эксцинтриситет ,  Затухающее колебание y = Ae-ax•sin(ωx+φ)

.    6. Задачи, решаемые методом дифференциального исчисления.

Дифференциальное исчисление — широко применяемый для экономического анализа математический аппарат. Базовой задачей экономического анализа является изучение экономических величин, записываемых в виде функций.

 Задачи, решаемые методом дифференциального исчисления:

1. в экономике очень часто требуется найти наилучшее, или оптимальное значение того или иного показателя: наивысшую производительность труда, максимальную прибыль, максимальный выпуск, минимальные издержки и т.д. Нахождение оптимального значения показателя сводится к нахождению экстремума функции.

2. задачи на экстремум функций нескольких переменных (т.к. экономические показатели обычно зависят от многих факторов). Многие задачи включают не только максимизируемую (минимизируемую) функцию, но и ограничения (скажем, бюджетное ограничение в задаче потребительского выбора). Это — задачи математического программирования.

3. важный раздел методов дифференциального исчисления, используемых в экономике, называется методами предельного анализа. Предельный анализ в экономике — совокупность приемов исследования изменяющихся величин затрат или результатов при изменениях объемов производства, потребления и т.п. на основе анализа, их предельных значений. Предельный показатель (показатели) функции у == f (х) — это ее производная (в случае функции одной переменной) или частные производные (в случае функции нескольких переменных).

4. часто требуется узнать, на какую величину вырастет результат, если будут увеличены затраты или, наоборот, насколько уменьшится результат, если затраты сократятся. С помощью средних величин ответ на этот вопрос получить невозможно. В подобных задачах требуется определить предел отношения приростов результата и затрат, т.е. найти предельный эффект.

5. предельная норма замены важна в задачах потребительского выбора (взаимозаменяемость благ), в задачах оптимизации производства (взаимозаменяемость труда и капитала) и в ряде других задач. Пусть y=f{x₁ x₂). Если мы хотим сохранить значение функции у неизменным, то это означает, что приращение у , а значит и его главная линейная часть должны быть равны нулю. Иными словами, о = dy = у'_X1 • d_X1 + у'_X2 • dx_X2. Отсюда предельная норма замены — - dx₁/dx₂ = Y’_X2/Y’_X1 , то      есть равняется отношению частных производных функции у по первому и второму факторам.

Методы дифференциального исчисления широко применяются не только для анализа взаимодействия отдельных экономических факторов, определения их взаимозаменяемости или оптимального сочетания, но и в сложных моделях экономики, в частности — в моделях экономической динамики.