4.2. Дисперсия и среднее квадратическое отклонение

Дисперсия и среднее квадратическое отклонение дают представление о разбросе случайных величин относительно их среднего значения.

4.2.1. Дисперсия случайной величины

Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

Для вычисления дисперсии можно использовать слегка преобразованную формулу

,

так как М(Х), 2 и – постоянные величины. Таким образом,

.

4.2.2. Свойства дисперсии

Свойство 1. Дисперсия постоянной величины равна нулю. Действительно, по определению

Свойство 2. Постоянный множитель можно выносить за знак дисперсии с возведением его в квадрат.

Доказательство

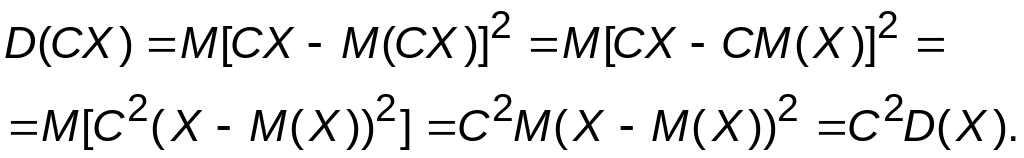
Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:

Центрированная величина обладает двумя удобными для преобразования свойствами:

Свойство 3. Если случайные величины Х и Y независимы, то

Доказательство. Обозначим . Тогда и .

Поэтому

Во втором слагаемом в силу независимости случайных величин и свойств центрированных случайных величин

,

поэтому

.

Пример 4.5. Если a и b – постоянные, то D(aХ+b)=D(aХ)+D(b)= .

4.2.3. Среднее квадратическое отклонение

Дисперсия, как характеристика разброса случайной величины, имеет один недостаток. Если, например, Х – ошибка измерения имеет размерность ММ, то дисперсия имеет размерность . Поэтому часто предпочитают пользоваться другой характеристикой разброса – средним квадратическим отклонением, которое равно корню квадратному из дисперсии

Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.

Пример 4.6. Дисперсия числа появления события в схеме независимых испытаний

Производится n независимых испытаний и вероятность появления события в каждом испытании равна р. Выразим, как и прежде, число появления события Х через число появления события в отдельных опытах:

Так как опыты независимы, то и связанные с опытами случайные величины независимы. А в силу независимости имеем

Но каждая из случайных величин имеет закон распределения (пример 3.2)

	0	1
Р	1-р	р

и (пример 4.4). Поэтому, по определению дисперсии:

,

где q=1-p.

В итоге имеем ,

Среднее квадратическое отклонение числа появлений события в n независимых опытах равно .

4.3. Моменты случайных величин

Помимо уже рассмотренных случайные величины имеют множество других числовых характеристик.

Начальным моментом k-го порядка случайной величины Х ( ) называется математическое ожидание k-й степени этой случайной величины.

Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени соответствующей центрированной величины.

Легко видеть, что центральный момент первого порядка всегда равен нулю, центральный момент второго порядка равен дисперсии, так как .

Центральный момент третьего порядка дает представление об асимметрии распределения случайной величины. Моменты порядка выше второго употребляются сравнительно редко, поэтому мы ограничимся только самими понятиями о них.