2. Повторные независимые испытания

2.1. Формула Бернулли

В теории вероятностей и ее приложениях большое значение имеет простая схема случайного эксперимента, которую называют схемой Бернулли, или схемой независимых испытаний. Испытания или опыты называют независимыми, если вероятность каждого исхода не зависит от того, какие исходы имели другие опыты, т.е. вероятность каждого исхода остается постоянной от опыта к опыту.

Пусть производится независимых опытов, в каждом из которых может появиться или не появиться событие A. Причем вероятность появления события в каждом опыте равна p, а вероятность непоявления равна: q=1–p. Требуется найти вероятность того, что в n независимых опытах событие A произойдет ровно k раз. В качестве примеров описанной схемы можно назвать бросание монеты (A – выпадение герба), стрельбу по цели в неизменных условиях (A – попадание в цель), изготовление деталей при заданном технологическом режиме (A – изготовление бракованной детали) и т.д.

Найдем вероятность . Все возможные случаи появления события A k раз в n опытах можно перебрать следующим образом. Возьмем k букв A и n- k букв и будем их между собой переставлять. Каждая перестановка соответствует определенной очередности появления или непоявления события A. Например, соответствует ситуации, в которой событие появилось в первом опыте, во втором и третьем не появилось, появилось в четвертом и т.д. Всего вариантов будет столько, сколькими способами можно из n мест выбрать k различных (порядок не важен) и поставить на них букву A, т.е. способов. Вероятность любого из этих способов (в силу независимости опытов, а значит, и событий) равна по теореме умножения вероятностей . Появление хотя бы одного из этих несовместных исходов приводит к появлению интересующего нас события, поэтому

или

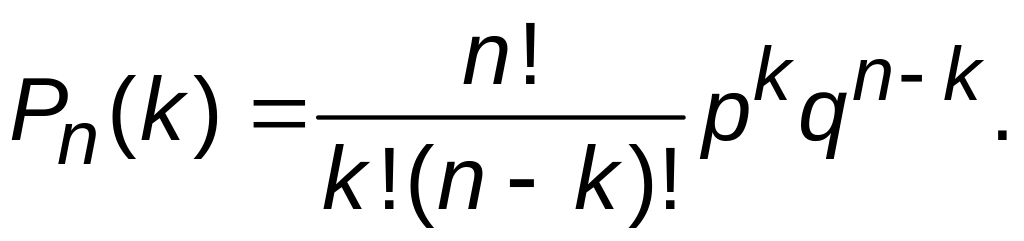
Это и есть формула Бернулли.

Замечание. При вычислении факториалов используют формулы: n!=1 , 1!=1, 0!=1.

Пример 2.1.

Хлебозавод выпускает изделий высшего сорта. Взяли наугад четыре изделия. 1) Какова вероятность того, что среди них только одно высшего сорта? 2) Хотя бы одно изделие высшего сорта?

Решение

В данном случае вероятность того, что взятая наугад буханка имеет высший сорт, равна p =  , не имеет: q= и не изменяется от изделия к изделию. Поэтому можно считать, что мы имеем дело со схемой независимых испытаний и можем воспользоваться формулой Бернулли.

1. .

2. Вторую вероятность легче вычислить с помощью противоположного события:

.

Вычислим все вероятности: , , , , и сравним их между собой. Для наглядности построим многоугольник распределения вероятностей. На горизонтальной оси отметим значения k , а на вертикальной – соответствующие им вероятности (рис 2.1).

Рис. 2.1.

Нетрудно видеть, что есть такое значение числа появления событий (k=3), которому соответствует наибольшая вероятность. Назовем такое значение наивероятнейшим и обозначим через k₀. Для небольших n можно отыскать наивероятнейшее значение простым перебором, но для больших n следует найти наиболее экономный способ.

Рассмотрим общий случай.

Зафиксируем n и убедимся в том, что с ростом k сначала возрастает, а потом, достигнув наибольшего значения при k=k₀ (которое может повториться дважды), убывает. Для этого рассмотрим отношение

Так как kq>0, то из полученного выражения следует

1) , если ;

2) , если ;

3) , если .

Итак, , но отстоит влево от не дальше чем на единицу (иначе между ними поместилось бы , которое, согласно неравенству, было бы наивероятнейшим). Поэтому . Так как k₀ – целое число, а длина интервала равна единице, то приходим к выводу: наивероятнейшим числом появлений события в n независимых опытах является целое число k₀, заключенное в пределах или . Наивероятнейших чисел будет два, если целое (рис. 2.2).

Рис. 2.2.

Пример 2.2.

а) Игральный кубик подбрасывается 50 раз. Каково наиболее вероятное число выпадения двух очков?

Здесь n=50, p=1/6, q=5/6.

Следовательно, k₀=8.

б) Если кубик подбрасывается всего 17 раз, то наивероятнейших чисел будет два, так как (целое число). В этом случае k₀=2 или k₀=3.