
10169
.pdf
60
P ω 2 = D * - статическая деформация (прогиб) от действия амплитудного
значения гармонической нагрузки.
Обозначая через |
μ = |
|
|
1 |
|
|
- динамический |
коэффициент, |
||||||
|
|
|
|
|
|
|||||||||
|
- λ2 )2 + γ 2 × λ2 |
|||||||||||||
|
(1 |
|
|
|
|
|
|
|
||||||
выражение (8.6) примет вид: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
A1 = μ × D * . |
|
|
|
|
|
|
(8.7) |
||
|
|
|
|
|
|
|
|
|
|
|||||
Если пренебречь силами сопротивления, то |
|
|
|
|
|
|
|
|||||||
y = A×sin (ω t + α ) + A × sinθ t , |
где: |
A = |
|
|
* |
. |
|
|||||||
1 |
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
1 |
− λ2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
При резонансе θ = ω , т.е. |
частота нагрузки |
совпадает |
с собственной |
|||||||||||
частотой. В этом случае λ = 1 и динамический коэффициент будет равен: μ = γ1 ,
аамплитуда вынужденных колебаний A1 ® ¥ , что не соответствует
действительности. Поэтому в этом случае необходимо учитывать силы сопротивления.
8.1. Коэффициент динамичности при гармонической
нагрузке и его анализ
Коэффициент динамичности μ показывает, во сколько раз динамический эффект (например, перемещение) превышает статический. В соответствии с (8.7)
динамический коэффициент представляет отношение амплитуды вынужденных колебаний к статической деформации от действия амплитудного значения гармонической нагрузки, т.е.:
μ = |
A |
= |
|
1 |
|
. |
(8.8) |
|
|
|
|
|
|||||
|
D * |
(1 - λ2 )2 + γ 2 × λ2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 8.2

61
Проанализируем полученное выражение
(8.8). С этой целью построим график зависимости коэффициента динамичности от отношения частот при различных значениях коэффициента неупругого сопротивления материала γ ( см. рис. 8.2). При λ → 0 , т.е.
при θ PP ω , коэффициент динамичности μ = 1
для всех видов материалов. Это означает,
что влияние гармонической нагрузки с амплитудным значением P в этом случае будет аналогично ее статическому действию.
-При λ → ∞ , т.е. когда θ FF ω , коэффициент
μ→ 0 вне зависимости от материала. Это
|
|
|
означает, что влияние гармонической |
|||||||||||
|
|
|
нагрузки в этом случае отсутствует. |
|
||||||||||
|
|
|
- При |
λ = 1 , |
θ = ω |
- условие резонанса. В |
||||||||
|
|
|
этом |
случае |
коэффициент |
динамичности |
||||||||
|
|
|
|
μ = |
1 |
является |
функцией |
коэффициента |
||||||
|
|
|
|
γ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
неупругого сопротивления материала и будет |
|||||||||||
Рис. 8.2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
составлять, |
например: для |
конструкций |
из |
стали |
μ = |
1 |
= 40, |
для |
||||||
|
||||||||||||||
0,025 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
конструкций |
из дерева |
μ = |
1 |
|
= 20, |
для |
железобетонных конструкций |
|||||||
|
|
|||||||||||||
|
|
|||||||||||||
0,05
μ = 1 = 10. 0,1
Как видно из графиков, на большей части диапазона λ функции изменения коэффициентов динамичности при разных значениях γ совпадают. В этой связи в расчетах на действие гармонической нагрузки учет сил неупругого сопротивления выполняют только в так называемой резонансной зоне, для
которой 0,85 ≤ ( λ = |
θ |
) ≤ 1,15 |
(8.9) . |
|
|
|
ω |
|
|
За пределами резонансной зоны коэффициент неупругого сопротивления материала можно не учитывать и определять коэффициент динамичности по формуле:

|
|
62 |
|
|
|
|
|
|
|
μ = |
|
1 |
|
= |
1 |
. |
(8.10) |
||
|
|
|
|
|
|||||
|
|
|
1 - λ2 |
||||||
(1 - λ2 )2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
9.Вынужденные колебания систем с конечным числом степеней свободы без учета сил сопротивления при действии гармонической нагрузки
Дифференциальные |
уравнения движения |
системы с “ |
n |
“ |
степенями |
|||||||
свободы при действии гармонической нагрузки Pi (t) = Pi × sin θ t , |
(i= |
1, |
2, …, n ) с |
|||||||||
одинаковой частотой θ и фазой без учета сил сопротивления имеют вид: |
||||||||||||
&& |
|
|
&& |
|
|
&& |
|
* |
|
|
|
|
+ M |
|
+...+ M n |
×δ1n |
+ y1 |
= D1P × sinθ t; |
|
|
|||||
M 1 ×δ11 × y1 |
2 ×δ12 × y2 |
× yn |
|
|
||||||||
.................................................................................................. |
|
|
(9.1) |
|||||||||
&& |
|
|
&& |
|
|
&& |
|
* |
|
|
||
|
|
|
|
|
|
|
|
|||||
+ M |
|
+ ...+ M n |
×δ in |
+ yi |
= DiP × sinθ t; |
|
|
|||||
M 1 ×δ i1 × y1 |
2 ×δ i 2 × y2 |
× yn |
|
|
||||||||
&& |
|
|
&& |
|
|
&& |
|
* |
|
|
|
|
|
|
+...+ M n |
×δ nn |
+ yn = DnP × sinθ t, |
|
|
||||||
M 1 ×δ n1 × y1 |
+ M 2 ×δ n 2 × y2 |
× yn |
|
|
||||||||
или в общем виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
∑δ ij |
× M j × y j + yi |
|
* |
|
|
|
|
|
(9.2) |
|
|
|
= DiP × sinθ t , |
|
|
||||||||
|
|
|
|
&& |
|
|
|
|
|
|
|
|
|
|
j =1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где: D*iP = ∑δ ij × Pj - |
прогиб в |
направлении |
оси |
yi , вызванный |
статическим |
|||||||
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
действием амплитудных значений гармонической нагрузки, с начальными
условиями y0i |
, y |
0i , (i = 1, 2, ..., n) при t = 0 . |
|
& |
|
Число уравнений (9.2) всегда равно степени свободы системы.
Решение этой системы дифференциальных уравнений складывается из
общего решения однородных уравнений и частного решения неоднородных уравнений, т.е. : yi = yi, собст.
Решение соответствующих однородных дифференциальных уравнений
получено ранее (см. п. 6.1 “Формы собственных колебаний”) и имеет вид:
n |
|
yi, с = ∑ ρik × A1k × sin (ωk t + α k ), (i = 1, 2, ... , n) . |
(9.3) |
k =1
Частное решение выражает вынужденные колебания системы, каждая масса которой совершает колебания по гармоническому закону с частотой нагрузки, и имеет вид:
yi, в = Ai × sinθ t, (i = 1, 2, ... , n) , (9.4).
Подставляя (9.4) в (9.1), получим систему алгебраических уравнений вида:
|
|
|
63 |
|
|
|
|
|
|
|
|
|
|
(M |
1 |
×δ |
11 |
×θ 2 |
-1) × A + M |
2 |
×δ |
12 |
×θ 2 × A +...+ M |
n |
×δ |
1n |
×θ 2 × A + D* |
|
|
|
1 |
|
2 |
|
n 1P |
||||||
.........................................................................................................
M |
1 |
×δ |
i1 |
×θ 2 × A + M |
2 |
×δ |
i 2 |
×θ 2 |
× A + ... + M |
n |
× |
δ |
in |
×θ 2 × A + D* |
||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
n |
i |
|||||||
M |
1 |
×δ |
n1 |
×θ 2 × A + M |
2 |
×δ |
n2 |
×θ 2 × A +...+ (M |
n |
×δ |
nn |
×θ |
2 -1) × A + D* |
|||||||
|
|
1 |
|
|
|
|
2 |
|
|
|
|
n |
n |
|||||||
(9.5)
из которой определяются все значения амплитуд
A1 , A2 , ... , An , характеризующих форму
|
вынужденных колебаний системы: |
A = - |
Di |
|
, |
|
|
|
|||||
|
|
|
i |
D0 |
|
|
|
|
|
|
|
||
(9.6). |
|
|
|
|
|
|
В (9.6) : |
D0 - определитель системы уравнений (9.5), а Di |
получается из |
||||
D0 заменой i − го столбца столбцом свободных членов. |
|
|
|
|
|
|
Таким образом, решением уравнений (9.2) будет: |
|
|
|
|
|
|
|
n |
|
|
|
|
|
yi |
= yi, собст. + yi, вынужд. = yi, с = ∑ ρik × A1k × sin (ωk t + α k ) + Ai |
× sinθ t . (9.7) |
|
|||
k=1
Вэтом выражение A1k и α k - постоянные в количестве 2n, определяемые
из начальных |
условий |
y0i , y0i , (i = 1, 2, ..., n) |
при |
t = 0 . |
Когда |
частота |
θ |
|||
|
|
|
& |
|
|
|
|
|
|
|
совпадает с одной из собственных частот ωi , определитель D0 |
|
|
||||||||
обращается в ноль, а амплитуды Ai |
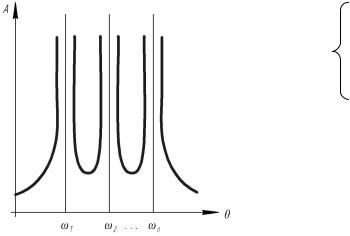
- в бесконечность. График зависимости Ai |
от |
||||||||
частоты |
θ в связи с этим будет иметь вид, показанный |
на |
рис. 9.1, из которого |
|||||||
видно, |
что |
система |
попадает |
в резонанс |
при |
каждом |
значении |
|||
θ = ωi , |
(i = 1, 2, ... , n). |
Нарастание |
амплитуд |
до |
бесконечности объясняется |
|||||
отсутствием сил неупругого сопротивления материала. |
В |
случае |
учета сил |
|||||||
сопротивления |
|
|
|
|
|
|
|
|
|
|
амплитуды будут иметь конечное значение. |
|
|
|
|
|
|
||||
10.Приближенные методы определения основной собственной частоты колебаний
Исследование систем с распределенными массами, степень свободы которых равна бесконечности, представляет в общем случае сложную математическую задачу. Однако, при динамическом расчете сооружений часто бывает возможно ограничиться рассмотрением только главных колебаний
64
основного тона. Поэтому широкое применение получили приближенные методы определения основной собственной частоты колебаний.
Энергетический метод. Формулы Рэлея.
При свободных колебаниях, если пренебречь силами сопротивления имеет место закон сохранения механической энергии
здесь  – потенциальная, а
– потенциальная, а 
 – кинетическая энергии системы при колебаниях.
– кинетическая энергии системы при колебаниях.
Если считать, что колебания отдельных точек системы около их положения равновесия происходят по гармоническому закону, то движение представляется
уравнением
где 



 – уравнение собственной
– уравнение собственной
формы колебаний.
Тогда все точки системы одновременно проходят через положение
равновесия, когда 



 ,
, 



 и кинетическая энергия – максимальна, а когда
и кинетическая энергия – максимальна, а когда
одновременно достигает крайних положений, где их скорости равны нулю, т.е.
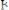



 и потенциальная энергия – максимальна.
и потенциальная энергия – максимальна.
Таким образом,
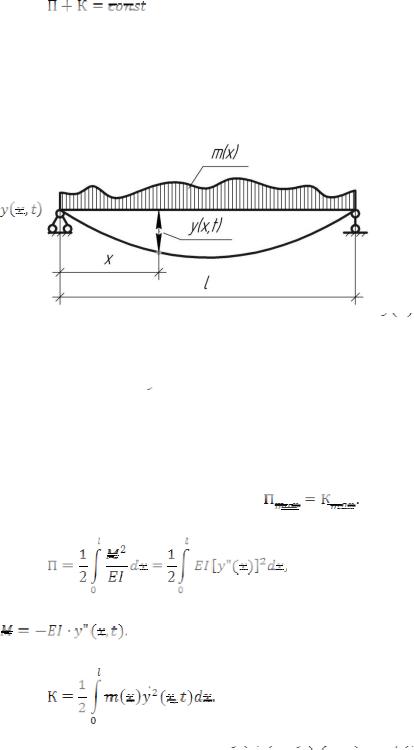
Потенциальная энергия системы при колебаниях будет
так как изгибающий момент
Кинетическая энергия системы равна
Вычислим производные от 
























 входящие в выражения потенциальной и кинетической энергии
входящие в выражения потенциальной и кинетической энергии

65
И определим максимальные значения потенциальной и кинетической энергии
Подставляя эти выражения в закон сохранения механической энергии получим формулу Рэлея для определения основной собственной частоты
Эта формула показывает, что если бы было известно точное уравнение формы собственных колебаний 



 , то при его постановке можно было бы получить точное значение собственной частоты.
, то при его постановке можно было бы получить точное значение собственной частоты.
Однако, уравнение формы колебаний неизвестно. Поэтому его задают приближенно. Принятая для решения собственная форма колебаний должна отвечать граничным условиям, т.е. условиям закрепления концов стержня.
При наличии в системе сосредоточенных масс 

 , формула будет иметь
, формула будет иметь
вид
Здесь 

 – ордината собственной формы колебаний в точке, где находится масса
– ордината собственной формы колебаний в точке, где находится масса 

 .
.
Часто уравнения собственной формы колебаний принимают подобным уравнению прогиба от статической нагрузки 











 , т.е. от сил тяжести,
, т.е. от сил тяжести,
соответствующих массам системы. При этом в выражение потенциальной энергии системы можно заменить более простым, численно равным выражением работы внешних сил, т.е. нагрузки 




Максимальное значение работы будет
Формула Рэлея запишется в виде

66
Если в системе кроме распределенной имеются сосредоточенные массы


 , то формула будет иметь вид
, то формула будет иметь вид
Способ приведенной массы
В этом способе система с бесконечной степенью свободы (рис. )
заменяется динамически эквивалентной системой с одной степенью свободы,
имеющей одну массу 

 , сосредоточенную в точке
, сосредоточенную в точке 
 (рис. )
(рис. )
Две системы будут динамически эквивалентными, если они имеют одинаковые кинетические энергии в любой момент времени.
Закон движения системы запишем в форме
Скорость колебаний
И кинетическая энергия системы будет
Соответственно, для системы с одной степенью свободы
Приравнивая выражения для кинетических энергий будем иметь
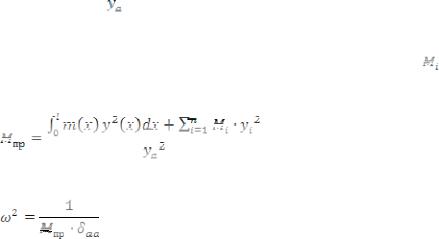
|
|
|
|
|
|
|
|
|
|
|
|
|
67 |
|
|
|
|
||||||||||
|
|
|
|
Здесь |
|
|
|
– ордината собственной формы |
|
колебаний |
точке, где |
||||||||||||||||
сосредоточена приведенная масса. |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
При наличии в системе сосредоточенных масс |
|
|
, формула будет иметь |
||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основная собственная частота колебаний определяется выражением
68
Список литературы
1.В. А. Киселев. Строительная механика. Спец. курс. М.: Стройиздат, 1980.
–616 с.
2.А. Ф. Смирнов, А. В. Александров, Б. Я. Лащенников и др. Строительная механика. Динамика и устойчивость сооружений. - М.: Стройиздат, 1984.
–416 с.
3.Н. И. Безухов, О. В. Лукин, Н. В. Колкунов. Устойчивость и динамика сооружений в примерах и задачах. – М.: Высшая школа, 1987. – 110 с.

69
Лампси Борис Борисович Юдников Сергей Георгиевич
УСТОЙЧИВОСТЬ И ОСНОВЫ ДИНАМИКИ СООРУЖЕНИЙ
Учебно-методическое пособие по подготовке к лекциям по дисциплине « Устойчивость и основы динамики
сооружений» для обучающихся по направлению подготовки 08.05.01 Строительство уникальных
зданий и сооружений специализация Строительство высотных и большепролетных зданий и
сооружений
Федеральное государственное бюджетное образовательное учреждение высшего образования « Нижегородский государственный архитектурно-строительный университет» 603950, Нижний Новгород, ул. Ильинская, 65.
http://www. nngasu.ru, srec@nngasu.ru
