
10169
.pdf
40
б) Стержень с двумя соединительными решетками Формула для определения критической силы получается из предыдущей, если в
ней заменить 
 на 2
на 2
 и
и 
 на 2
на 2
 , т.е. здесь следует учитывать обе системы соединительных решеток
, т.е. здесь следует учитывать обе системы соединительных решеток
8.Устойчивость стержней с планками
Рассмотрим стержень с планками. Полагая, что нулевые точки эпюры изгибающих моментов, в случае деформации стержня, будут на середине расстояний между планками. Вырежем элемент длиной а. Относительный сдвиг будет 








 .
.
Удельное перемещение 

 получим по правилу Верещагина, рассматривая участок стержня, как раму. Построим эпюру изгибающих моментов и перемножим ее на себя
получим по правилу Верещагина, рассматривая участок стержня, как раму. Построим эпюру изгибающих моментов и перемножим ее на себя



















 =
=


Здесь 

 – жесткость ветви,
– жесткость ветви, 

 – жесткость планки, соединяющих ветвей. Тогда получим
– жесткость планки, соединяющих ветвей. Тогда получим

 =
=
Подставляя в формулу для Ркр, получим выражение для критической силы
41
II. Динамика стержневых систем
1.Динамические расчеты конструкций
Динамика сооружений – это раздел строительной механики, изучающий колебания упругих систем и, соответственно, методы определения усилий и деформаций в конструкциях, подверженных действию динамических нагрузок.
Динамика сооружений возникла на базе аналитической механики и теории колебаний. На их основе были решены многие важные задачи: колебания маятника, явление удара, колебания стержня и систем с конечным и бесконечным числом степеней свободы. Дальнейшее развитие теории расчета сооружений на динамические нагрузки привело к возникновению ряда специальных направлений:
динамики стержневых систем, пластин, оболочек, динамики оснований и фундаментов и других.
Многие воздействия на сооружения носят ярко выраженный динамический характер. При этих воздействиях сооружения приходят в движение и, хотя перемещения оказываются в большинстве случаев небольшими, скорости и,
главное, ускорения могут достигать величин, опасных для конструкций и для сооружения в целом. К подобным воздействиям относятся сейсмические толчки,
ветровые порывы, а также, например, динамические воздействия технологического происхождения: движение неуравновешенных частей машин и механизмов, движение поездов, кранов и т.п.
Как известно из курса механики, ускоренные или замедленные движения масс вызывают инерционные силы, действующие на конструкцию так же, как и статические нагрузки. Поэтому задачей динамического расчета сооружения является определение инерционных сил, появляющихся при динамических воздействиях.
Особенностью динамических нагрузок является то, что в большинстве случаев они вызывают колебания. При периодическом повторении малых динамических воздействий в определенных условиях происходит накопление энергии системы, выражающееся в постепенном увеличении амплитуды колебаний, а вместе с ней и интенсивности инерционных сил до очень больших размеров. Это явление, называемое резонансом, особенно опасно для сооружений тем, что разрушение может произойти при малых воздействиях и в
42
конструкциях, достаточно прочных по отношению к обычным статическим
нагрузкам.
Существенным отличием динамических методов расчета от статических является введение нового переменного – времени, которое участвует в уравнениях либо в явном виде, либо в виде производных от неизвестных функций по времени. Обычно там, где статическая задача решается при помощи обычных алгебраических или трансцендентных уравнений, соответствующая динамическая задача требует уже решения дифференциальных уравнений с производными по времени. Именно в этой связи динамические расчеты сооружений существенно
сложнее статических.
В динамике сооружений, как и в статике сооружений, оперируют не с действительными конструкциями, а с их расчетными схемами. Особенностью этих расчетных схем является обязательный учет массы конструкции, а также ее
упругих свойств.
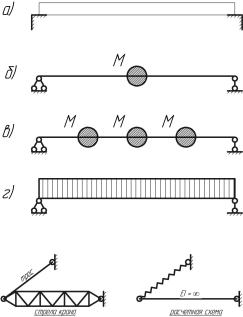
Так, например, при расчете систем, преимущественно работающих на изгиб, расчетные схемы представляются в
виде идеально упругих невесомых балок, а
массу конструкции сосредотачивают в одной или нескольких точках, или же считают массу
равномерно-распределенной |
по всей длине |
|
балки (рис. 1.1). |
Для |
конструкции, |
имеющей большую изгибную жесткость и опирающейся с одной стороны на упругую
опору (рис. 1.2), расчетная схема может быть представлена в виде стержня бесконечной жесткости, шарнирно прикрепленного с одной стороны и имеющего упругую связь с другой стороны.
Задачами динамического расчета являются:
-определение динамических перемещений и скоростей с целью установления возможности их допущения для выполнения нормального технологического процесса и установления допустимых колебаний для различных условий жизни человека (производственных, жилищно-бытовых и т.п.);
-обеспечение несущей способности сооружения, которое производится из предельного условия:
43
N max (t) ≤ φ ,
где: N max (t) - максимальные усилия, деформации или напряжения,
возникающие в элементах сооружения при колебаниях;
φ- предельно допустимые величины, устанавливаемые из условий
прочности, устойчивости, жесткости и выносливости.
Расчет упругих систем на динамическую нагрузку производят в следующей
последовательности:
-назначают расчетную схему сооружения для выполнения динамического расчета;
-определяют нагрузки, действующие на систему;
-составляют дифференциальное уравнение движения системы, решая которое получают уравнение движения системы;
-исследуют уравнение движения системы и находят максимальные значения усилий, деформаций, напряжений.
2. Степень динамической свободы систем
Степенью динамической свободы системы называется число независимых геометрических параметров (обобщенных координат),
определяющих положение всех масс системы в любой момент времени при любом ее движении. По сравнению со статикой, в динамике сооружений задача определения степени свободы системы значительно усложняется. Строго говоря,
любые сооружения вследствие их деформативности и распределения собственной массы вдоль осей всех стержней будут системами с бесконечным числом степеней свободы. В связи со сложностью расчета таких систем, при решении практических задач пользуются упрощенными схемами с конечным числом степеней свободы, стремясь как можно больше понизить это число. Так в системах, преимущественно работающих на изгиб (балки, рамы и др.), обычно пренебрегают малыми продольными и угловыми деформациями в сравнении с большими изгибными, а также малыми распределенными массами в сравнении с большими сосредоточенными, например массой балки в сравнении с массой расположенного на ней оборудования. Практически, степень свободы определяют минимальным количеством условных дополнительных связей,
которые нужно ввести в расчетную схему, чтобы полностью устранить
44
возможность перемещений масс системы, пренебрегая при этом
перемещениями второго порядка малости. |
|
|
|
|
|
|
|
Пример 1. Определить степень свободы W |
|||||
|
системы, |
состоящей |
из |
двутавровой |
балки |
|
|
№ 36 (g = 0,7кН / м) пролетом |
2,0 |
м с |
|||
|
установленным на |
ней |
электродвигателем |
|||
|
массой 7,0 тонн (рис. 2.1). |
|
|
|
||
|
Решение. |
Балка с |
включенным |
двигателем |
||
|
совершает колебания. Масса двигателя, |
|||||
|
заключенная в небольшом объеме, в 50 раз |
|||||
|
больше массы балки, распределенной по ее |
|||||
|
длине. В связи с этим определяющей движение |
|||||
Рис. 2.1 |
системы будет масса двигателя, а саму балку |
|||||
|
при этом можно считать невесомой. |
|
|
|||
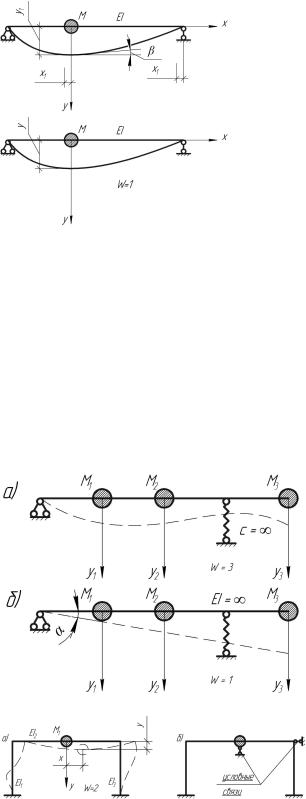
Если учесть, что углы поворота балки малы (а при расположении двигателя в середине пролета угол поворота сечений вообще равен нулю) и исключить из рассмотрения горизонтальные перемещения, обусловленные продольной деформацией балки, приходим к упрощенной расчетной схеме, которая является системой с одной степенью свободы.
Пример 2. Определить степень динамической свободы W системы,
изображенной на рис. 2.2.
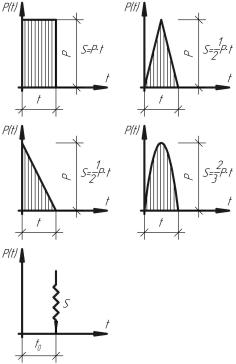
Рис. 2.2 |
Пример 3 Пренебрегая продольными |
|
|
|
деформациями, определить степень |
|
динамической свободы W системы, |
|
изображенной на рис. 2.3. |
Рис 2.3 |
|
45
3. Динамические нагрузки
Динамическими называют нагрузки, величина, направление или точки приложения которых изменяются во времени настолько быстро, что в элементах конструкции возникают силы инерции. Силы инерции возникают вследствие сообщения массам сооружения ускорений при колебаниях.
Динамические нагрузки характеризуются законом изменения во времени
P(t). В том случае, если этот закон может быть представлен в аналитическом или,
хотя бы, в графической зависимостях, динамическую нагрузку называют хорошо определенной или детерминированной. В том случае, если закон изменения динамической нагрузки не может быть задан аналитически, но возможно его представление через теорию случайных функций, нагрузка называется случайной
или недетерминированной.
К детерминированным нагрузкам относятся:
- импульсивные нагрузки
Импульсивными называют внезапно приложенные и быстро исчезающие нагрузки, продолжительность действия которых мала в сравнении с периодом основного тона собственных колебаний (t ≤ 0,1 T , где T − период собственных колебаний) . Выделяют однократный, повторяющийся и периодический
импульс. Импульсы различаются по форме и могут быть прямоугольными, треугольными,
параболическими и др. – см. рис. 3.1. Значение однократного импульса равно площади
t
соответствующих фигур S = ∫ P(t)dt .
0
Периодический импульс состоит из одинаковых импульсов, повторяющихся через равные промежутки времени, называемые периодом Ts (рис. 3.2). Импульсивные нагрузки возникают от работы вырубных прессов, штамповочных автоматов, долбежных станков, а также при движении транспорта.
Эффект действия импульсивных нагрузок
Рис. 3.1
определяется только величиной импульса и не

Рис. 3.2
Рис. 3.3
Рис.3.4
Рис. 3.5
46
зависит от его амплитуды и закона изменения во времени
- Ударные нагрузки создаются при ударе тел конечной массы о сооружение, чаще всего при падении тел (рис. 3.3). Такие нагрузки возникают при работе копров, молотов,
подъеме или складировании тяжелых деталей.
В отличии от нагрузки импульсивной в этом случае к массе сооружения добавляется масса ударяющегося тела. Длительность действия ударных нагрузок - t = ( 0,1 ¸ 3,0) T. Эффект действия этих нагрузок существенно зависит от амплитуды, закона изменения во времени и относительной длительности. Как правило,
ударные нагрузки задаются в виде функции или графика.
- Простые гармонические (вибрационные)
нагрузки возникают как правило при вращении неуравновешенных масс – частей механизмов
имашин: вентиляторов, центрифуг,
вибраторов, компрессоров, электромоторов.
Этот вид нагрузок изменяется по законам
(рис.3.4):
P(t) = P × sin (θ t + α ) ; |
|
|
P(t) = P × cos (θ t + α ) |
, |
(3.1) |
где: P - амплитуда нагрузки; |
θ |
- круговая |
частота, т.е. число изменений нагрузки в |
2π |
||||||||
сек.; |
(θ t + α ) - фаза; |
α - |
начальная фаза; |
||||||
Tp = |
2π |
- период, т.е. |
время одного полного |
||||||
θ |
|||||||||
|
|
|
|
|
|
|
|
||
изменения гармонической нагрузки. |
|
|
|
||||||
Величина обратная периоду |
fp = |
1 |
= |
θ |
[гц] |
||||
Tp |
2π |
||||||||
|
|
|
|
|
|
|
|||
характеризует число изменений нагрузки в секунду и измеряется в герцах.
47
Выразим основные параметры гармонической нагрузки. С этой целью
рассмотрим деталь машины, вращающейся равномерно с угловой скоростью θ и |
||
неуравновешенной массой M на расстоянии |
r от оси вращения (рис.3.5). |
|
Нормальное ускорение W = -r ×θ 2 , направленное |
к оси вращения, создает |
|
центробежную силу инерции P = - M ×W = M × r ×θ 2 , |
(3.2). |
Сила P постоянна по |
модулю, если пренебречь малой величиной r |
в сравнении с размерами |
|
сооружения, но изменяет свое направление при вращении в зависимости от |
угла |
(θ t + α ) . Проектируя силу P на оси координат, получим выражения |
для |
вертикальной Py и горизонтальной Px составляющих нагрузки, совпадающие с
(3.1). Таким образом, при вращении детали механизма с неуравновешенной массой, на сооружение действуют две гармонические силы, отличающиеся по
фазе на π . Круговая частота гармонической нагрузки совпадает с угловой
2
скоростью вращения, а амплитуда определяется выражением (3.2).
n
- Сложные гармонические нагрузки P(t) = ∑ Pi × sin(θi t + α i ) . Этот вид
i=1
загружения создается механизмами с кривошипно-шатунными механическими схемами – поршневые компрессоры, лесопильные рамы и др.
- Подвижные нагрузки создаются в результате перемещения механизмов или машин по строительным конструкциям.
К случайным или недетерминированным нагрузкам относятся:
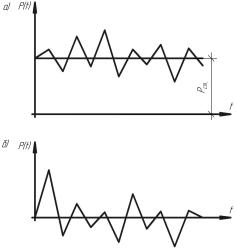
- ветровая нагрузка. Она имеет статическую и динамическую составляющие (рис. 3.6а). Статическая составляющая учитывает установившийся скоростной напор ветра. Ее необходимо определять при расчете любых зданий и сооружений. Динамическая составляющая характеризует пульсацию скоростного напора ветра вследствие его порывов и учитывается при расчете высотных сооружений: башен,
теле-радио мачт, высотных зданий с высотой
более 40 м.
Рис. 3.6
48
-сейсмическая нагрузка. Она возникает в результате колебаний грунта при землетрясениях и носит случайный характер. Эта нагрузка не имеет статической составляющей (рис. 3.6б).
Кроме рассмотренных существуют и другие виды динамических нагрузок,
оказывающих существенное влияние на процесс колебания сооружений.
4. Понятие о коэффициенте динамичности
Достаточно сложные динамические расчеты на практике стремятся привести специальными приемами к более простым статическим расчетам.
Одним из таких способов является введение коэффициента динамичности μ .
Коэффициент динамичности показывает во сколько раз динамический эффект превышает статический. Он определяется в зависимости от вида действующей динамической нагрузки.
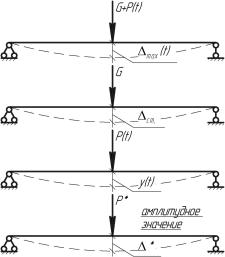
Рассмотрим упругую систему, находящуюся под действием статической нагрузки G и
динамической нагрузки P(t). Выразим величину
максимального прогиба системы |
|
max (t) . |
|
|||
По принципу независимости действия сил: |
|
|||||
max (t) = |
ст. + y(t) ; |
y(t) = μ × D * , |
где: |
|
||
D * - |
прогиб |
от |
амплитудного значения |
|||
динамической нагрузки. Поэтому: |
|
|
|
|||
|
Dmax (t) = Dст. + μ × D * . |
|
|
|||
Аналогично |
выражаются |
усилия |
от |
|||
динамической нагрузки:
Рис. 4.1
Smax (t) = Sст. + μ × S * .
5. Колебания систем с одной степенью свободы
При колебаниях систем различают свободные и вынужденные колебания.
Вынужденными называют колебания, вызванные воздействием возмущающей силы.
Свободными называют колебания, вызванные начальными возмущениями.
В динамике сооружений под начальными возмущениями понимают либо начальную скорость, либо начальное перемещение.

49
Пусть на систему с одной степенью свободы действует динамическая нагрузка P(t) рис. 5.1. В момент времени t на массу M будут действовать силы:
- собственный вес массы Q = m × g = C × yст ;
-возмущающая сила P(t);
-восстанавливающая сила упругости (уп-
ругое сопротивление балки):
|
|
|
|
|
|
|
|
|
Fy = C × ( yст + y) ; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
- сила сопротивления среды (ее изме- |
|||||||||||
|
|
|
|
|
нение считают пропорциональным скорос- |
|||||||||||
|
|
|
|
|
ти движения системы): |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
& |
|
& |
dy |
- скорость; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Fc = b × y , y = |
dt |
||||||||
|
|
|
Рис. 5.1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
- сила инерции Fи |
= M |
×W |
= M × y , |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
&& |
|
|
&& |
= |
d 2 y |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
dt 2 |
|
- ускорение; C - |
коэффициент |
|
жесткости |
системы, численно |
||||||||||
где: W = y |
|
|
||||||||||||||
равный силе, |
которую нужно |
приложить к |
массе, |
чтобы |
ее перемещение |
|||||||||||
равнялось 1. Коэффициент жесткости “C” связан c удельным перемещением точки приложения массы выражением C = 1/ δ11 , где δ11 - перемещение точки приложения сосредоточенной массы от единичного значения силы P, приложенной в этой
точке в направлении возможного перемещения массы; g = 9,81м/ с2 - ускорение
свободного падения, b − коэффициент пропорциональности.
Применяя принцип Даламбера (“движущуюся систему масс можно считать уравновешенной, если кроме действующих на них сил приложить силы инерции,
равные Fи = M ×W = M × &y& ”) и используя условие равновесия в виде ∑Y = 0 ,
получим дифференциальное уравнение движения системы с одной степенью свободы:
M × y + C × ( yст |
+ y) + b × y - C × yст - P(t) = 0 , или |
M × y + b × y + C × y = P(t) . |
(5.1) |
||
&& |
& |
&& |
& |
|
|
5.1.Свободные колебания системы с одной степенью свободы без учета сил сопротивления
Если в уравнении (5.1) принять P(t) =0, то получим дифференциальное
уравнение движения системы при свободных колебаниях без учета сил
