
10169
.pdf
20
Будем рассматривать рамы, составленные только из прямолинейных стержней и загруженные только узловой нагрузкой. В этом случае при значениях сил меньших критической величины все стержни остаются прямолинейными.
Следовательно, устойчивой формой равновесия остается прямолинейная форма стержней. В критическом состоянии прямолинейная форма перестает быть устойчивой и становится возможной искривленная (деформированная) форма равновесия. Для определения этой формы необходимо найти обычные неизвестные метода деформаций – углы поворота узлов и их линейные перемещения.
Например, на рис. 2.1 показана рама,
неизвестными в которой по методу перемещений будут шесть углов поворота свободных жестких узлов и два линейных система будет иметь, следовательно, шесть заделок
и два опорных стержня, препятствующих линейным смещениям.
Канонические уравнения составим для деформированного состояния рамы,
которое наступит при критическом значении нагрузки. Так как нагрузка приложена в узлы, то она не вызовет во вновь введенных связях основной системы никаких реакций, следовательно уравнения будут однородными:
r11 × Z1 + r12 × Z 2 + ... + r1n × Z n = 0 ;
r21 × Z1 + r22 × Z 2 + ... + r2n × Z n = 0 ;
………………………………….. (2 .1) rn1 × Z1 + rn 2 × Z 2 + ... + rnn × Z n = 0 .
В этих уравнениях Z1 , Z 2 , ... , Z n - неизвестные углы поворота и линейные смещения.
Смысл уравнений остается тот же, что и при статическом решении задачи по методу перемещений, а именно: суммарная реакция в любой введенной
(дополнительной) связи должна быть равна нулю.
Для того, чтобы система имела решение, отличное от нуля, т.е. для того,
чтобы рама кроме прямолинейного, могла иметь уравновешенное деформированное состояние, необходимо, чтобы определитель системы (2.1)
был равен нулю:

21
r11 r12 . . . r1n
D = |
r21 |
r22 . . . |
r2n |
= 0 . (2.2) |
|
. . . . . . . . . . . . . . . |
|
||
|
rn1 |
rn 2 . . . |
rnn |
|
Между коэффициентами rik |
системы уравнений (2.2) и коэффициентами rik |
|||
обычных уравнений метода перемещений существует принципиальное отличие,
вытекающее из самой природы рассматриваемой задачи. В обычных уравнениях коэффициенты rik не зависят от внешней нагрузки: нагружена система или нет, -
для того, чтобы вызвать в данном закреплении данное перемещение, всегда требуется одно и то же усилие. В задаче об устойчивости во внимание принимаются те изгибающие моменты, которые возникают от продольной силы после того, как стержень принял криволинейную форму. Поэтому для единичного поворота или смещения конца стержня, нагруженного продольной силой, требуется иное усилие rik , чем для незагруженного. Эти коэффициенты являются функциями продольных сил.
Например, чтобы повернуть конец сжатого стержня на угол, равный
единице (рис. 2.2), требуется, очевидно, тем меньшее значение момента r11 |
, чем |
|||||
сильнее |
сжат |
стержень. |
Продольная |
|||
сжимающая сила как бы уменьшает жесткость |
||||||
стержня при работе его на изгиб. |
В обычном |
|||||
методе перемещений мы не можем подчинить |
||||||
коэффициенты rik |
требованию D = 0 , |
так как |
||||
они являются величинами постоянными. При |
||||||
этом |
можно доказать, |
что для |
них |
всегда |
||
D F 0 , |
а |
условие |
D = 0 никогда не |
выпол- |
||
няется. |
В задаче |
об |
устойчивости, где |
|||
коэффициенты являются функциями |
продольных |
сил, условие |
D = 0 |
|||
позволяет определить критическое значение этих сил.
Для определения критической нагрузки методом перемещений введем
следующие допущения:
- рассматривается только узловая нагрузка, не вызывающая поперечного
изгиба стержней;
22
-все стержни системы считаются несжимаемыми и нерастяжимыми. Это позволяет считать расстояние между узлами стержня до и после деформации системы постоянным;
-при определении поперечных сил не учитывается изменение угла
наклона сечения за счет изгиба стержня;
-при вычислении перемещений учитываются сжимающие силы,
возникающие в стержнях до деформации системы. Влияние приращений продольных сил в момент потери устойчивости не учитывается.
Первое допущение вызвано тем, что рассматривается потеря устойчивости только первого рода. Наличие вне-узловой нагрузки вызывает продольно-поперечный изгиб стержней рамы, при этом будет иметь место потеря устойчивости второго рода.
Последние три допущения обусловлены тем, что при потере устойчивости деформированная форма равновесия отличается от исходной формы весьма малыми перемещениями.
Реакции во вновь введенных связях и входящие в уравнение устойчивости определяются из уравнений равновесия той или иной (соответствующей)
отсеченной части системы. Но для их определения необходимо знать выражения концевых усилий в сжато-изогнутых стержнях основной системы метода деформаций от единичных угловых и относительных линейных смещений концов стержней при различных типах их закреплений.
2.1. Усилия и деформации сжато-изогнутого стержня
Рассмотрим стержень, сжатый двумя равными и противоположно
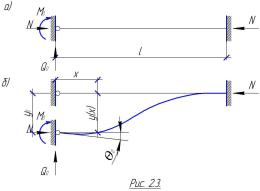
направленными силами N (см. рис. 2.3). Стержень имеет постоянную по длине l
жесткость EI . На рис. 2.3а стержень изображен прямолинейным в состоянии
неустойчивого (прямолинейного) равновесия, когда N N кр. , не превышая ее значение. На рис. 2.3б изображена устойчивая криволинейная форма равновесия стержня, когда N ³ N кр.
При потере устойчивости стержня сила N
|
|
|
23 |
|
|
|
|
|
|
|
|
может несколько измениться, но так как мы |
|||||
|
|
|
считаем |
отклонение |
от |
первоначальной |
||
|
|
|
формы бесконечно малым, то приращением |
|||||
|
|
|
N по сравнению с N можно пренебречь. |
|||||
|
|
|
Допустим, что в момент потери устойчивости |
|||||
|
|
|
стержня его левая опора переместилась на |
|||||
|
|
|
величину |
y0 , при этом |
опорное |
сечение |
||
|
|
|
стержня |
повернулось |
на |
угол θ0 |
и в нем |
|
|
|
|
возникли реактивные усилия - момент M 0 и |
|||||
|
|
|
поперечная сила Q0 . |
Величины y0 , θ0 , M 0 |
||||
|
|
|
и Q0 называют начальными параметрами. |
|||||
Составим дифференциальное уравнение изогнутой оси стержня: |
|
|||||||
y // = - |
M (x) |
= - [M |
0 + Q0 × x + N × ( y - y0 )] × |
1 |
, |
(2.3) |
|
|
|
EI |
|
||||||
|
EI |
|
|
|
|
|
||
где знак минус перед скобкой соответствует принятому правилу знаков, при котором положительным значениям изгибающих моментов соответствуют отрицательные значения второй производной от прогиба и наоборот. Если
обозначить |
n 2 = |
N |
|
|
|
|
и |
подставить |
|
в |
(2.3), |
|
то |
получим |
неоднородное |
|||||||||||||||||||
EI |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
дифференциальное уравнение изгиба второго порядка: |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y // + n 2 × y = |
|
N |
× y0 |
- |
M 0 |
|
- |
Q0 |
|
× x . |
|
|
|
(2.4) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
EI |
|
EI |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Общее решение этого уравнения состоит из решения однородного |
|||||||||||||||||||||||||||||||||
дифференциального |
уравнения |
y0 |
= A × sin nx + B × cos nx |
и |
частного решения |
|||||||||||||||||||||||||||||
неоднородного уравнения, которое отыскивается в виде: |
|
|
y1 = Сx + D . |
В |
||||||||||||||||||||||||||||||
приведенных |
|
выражениях |
A, |
B, |
С |
|
и |
|
|
D |
- |
|
|
постоянные |
интегрирования, |
|||||||||||||||||||
определяемые из граничных условий. |
|
После определения постоянных |
||||||||||||||||||||||||||||||||
интегрирования и выполнения некоторых преобразований, |
получим уравнение |
|||||||||||||||||||||||||||||||||
оси сжато-изогнутого стержня в следующим виде: |
|
|
|
|
|
|
||||||||||||||||||||||||||||
y(x) = y0 + θ0 |
× |
sin nx |
- |
M 0 |
× (1 - cos nx) - |
|
Q0 |
|
× (nx - sin nx) , или учитывая, что n 2 = |
N |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
EI |
|||||||||||||||||||||||||||
|
|
|
n |
N |
|
|
|
|
|
|
n × N |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
y(x) = y0 |
+ θ0 × |
sin nx |
- |
|
M 0 |
× (1 - cos nx) - |
|
Q0 |
|
× (nx - sin nx) |
(2.5) |
|
|
||||||||||||||||||||
|
n2 × EI |
n3 × EI |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

24
Уравнения для угла поворота θ (x) оси стержня в произвольном сечении,
расположенном на расстоянии " x" от левой опоры, а также изгибающего момента и поперечной силы могут быть получены из выражения (2.5):
θ (x) = y / (x) = θ0 × cos nx - [ |
M 0 |
× sin nx + |
Q0 |
× (1 - cos nx)] × |
1 |
; |
|
|||
|
||||||||||
n |
n2 |
|
|
|||||||
|
|
|
|
|
|
EI |
|
|||
M x |
= - EI × y // (x) = EI ×θ0 × n × sin nx + M 0 × cos nx + |
Q0 |
× sin nx ; |
(2.6) |
||||||
|
||||||||||
|
= - EI × y /// (x) = EI × n 2 × θ0 × cos nx - M 0 |
|
n |
|
|
|
||||
Qx |
× n × sin nx + Q0 |
× cos nx . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Используя выражения (2.5) и (2.6) можно определить реакции стержней,
загруженных продольной силой, при различных условиях их закрепления по
концам.
Например, для стержня с жестко защемленными по концам обеими
опорами, при повороте левой опоры на |
угол |
θ0 |
= 1 , |
при |
y0 = 0 |
и при |
неподвижной правой опоре (т.е. при x = l, |
θb |
= 0; |
yb |
= 0 ), |
можно |
получить |
значения изгибающего момента и поперечной силы на опоре “0” в следующем виде:
M 0 = 4 × i ×ϕ2 (V ) ; |
|
||||
|
|||||
Q0 |
= - |
6 × i |
×ϕ |
4 (V ) . |
(2.7) |
|
|||||
|
|
l |
|
|
|
На противоположном конце стержня, используя выражения (2.6) и (2.7),
получим следующие выражения момента и поперечной силы:
M b = 2 × i ×ϕ3 (V ) ;
|
|
Qb = - |
6 × i |
×ϕ |
4 (V ) . |
(2.8) |
||||||
|
|
|
||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В |
выражениях (2.7) и |
(2.8) V = l |
|
× |
|
Ni |
, i = |
EI i |
- погонная жесткость |
|||
i |
|
|
|
|
||||||||
|
|
i |
|
|
EIi |
|
li |
|||||
|
|
|
|
|
|
|
|
|
||||
стержня, |
а ϕi (Vi ) ( и ηi (Vi ) |
- см. таблицу 2.1) |
- функции А. Ф. Смирнова, для |
|||||||||
которых получены аналитические выражения, табулированные в функции параметра Vi .
Аналогичные выражения значений концевых реактивных моментов и поперечных сил могут быть получены при других закреплениях стержня по концам, а также при относительном линейном смещении опор.
25
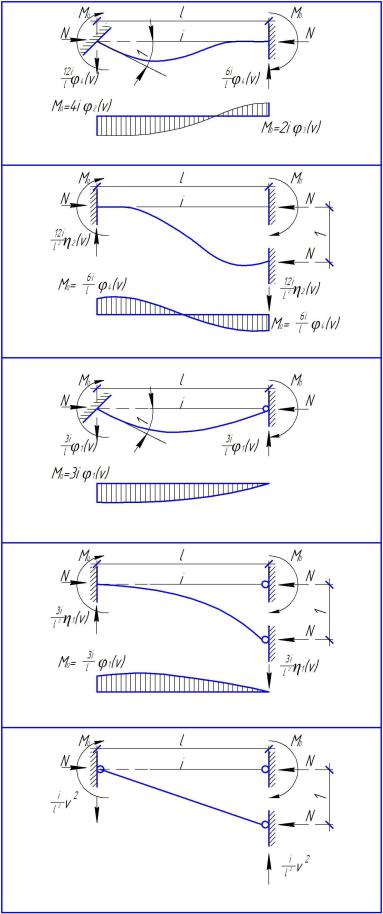
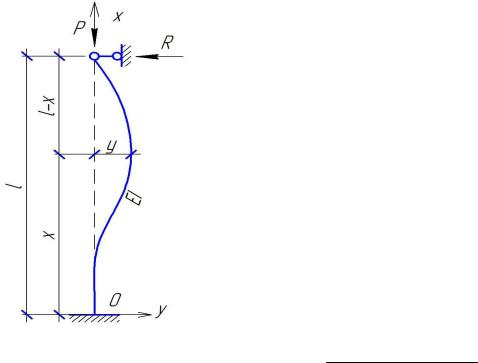
В таблице 2.1 приведены значения концевых усилий в сжато-изогнутом стержне при различных условиях его закрепления по концам от единичных значений углов поворота опор и их линейных смещений.
26
Таблица 2.1.
27
3. Устойчивость прямых однопролетных стержней
Определение критических сил и форм потери устойчивости прямых однопролетных стержней конечной жесткости, т.е. обладающих бесконечным числом степеней свободы, выполняется статическим или энергетическим методами. Система с бесконечным числом степеней свободы имеет бесконечное количество значений критических сил и соответствующих им форм деформированного состояния равновесия. При этом система однородных алгебраических уравнений будет содержать большое число неизвестных, но может быть заменена одним дифференциальным уравнением; обращение определителя в ноль приводит к характеристическому уравнению бесконечно высокой степени, т.е. к трансцендентному уравнению. Применение статического и энергетического методов определения критических сил рассмотрим на примерах.
3.1. Определение критической нагрузки для однопролетных
стержней статическим способом
Пример. Определить критическую силу для стержня с одним
защемленным и другим шарнирным концами (см. рис. 3.1). |
|
|
|||||||||||
Рассмотрим |
|
деформированную |
форму |
||||||||||
равновесия, |
используя дифференциальное |
||||||||||||
уравнение изогнутой оси стержня: |
|
|
|||||||||||
|
|
|
y // = - |
|
M |
|
|
. |
|
(3.1) |
|||
|
|
|
EI |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||
В этом выражении M - |
изгибающий момент в |
||||||||||||
произвольном сечении, расположенном на |
|||||||||||||
расстоянии “x” |
от одной из опор (см. рисунок): |
||||||||||||
|
|
M = -P × y - R × (l - x). |
|
(3.2) |
|||||||||
Подставляя (3.2) в (3.1) |
получим: |
|
|
||||||||||
y // = - |
P |
× y - |
R |
× (l - x) , |
|
или |
с |
учетом |
|||||
|
|
||||||||||||
|
EI |
EI |
|
|
|
|
|||||||
обозначения |
n 2 = |
P |
, |
|
(3.3), получим: |
||||||||
|
|||||||||||||
|
|
|
|
|
EI |
|
|
|
|
||||
|
|
y // + n 2 × y = |
|
R |
(x - l) . |
|
(.3.4) |
||||||
|
|
|
|
|
|||||||||
EI
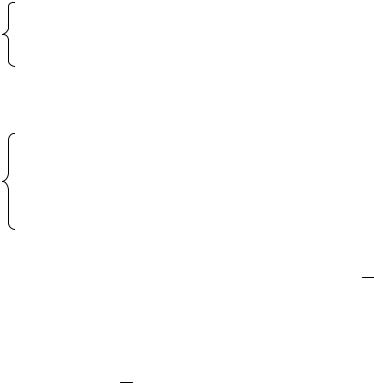
28
Получили неоднородное дифференциальное уравнение второго порядка,
решение которого |
складывается |
|
из |
суммы |
решений y = y0 + y1 , где: |
||||||||||||||||
y0 |
= A × sin nx + B × cos nx |
- общее |
решение соответствующего |
однородного |
|||||||||||||||||
дифференциального уравнения; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y1 =C × (x - l) - |
частное решение неоднородного дифференциального уравнения. |
||||||||||||||||||||
Подставляя частное решение неоднородного дифференциального |
|||||||||||||||||||||
уравнения в (3.4), будем иметь: |
y // = 0 , |
|
или: |
|
|
P |
× C × (x - l) + |
R |
× (l - x) = 0 , |
||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
EI |
|||
откуда |
C = |
R |
. |
Тогда общее решение примет вид: |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y = A × sin nx + B × cos nx + |
R |
(x - l). |
(3.5) |
||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
||
В |
выражении |
(3.5) |
A, B |
и |
C = |
R |
|
- произвольные |
постоянные, |
||||||||||||
P |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
определяемые из граничных условий (условий закрепления концов стержня). При закреплении стержня по концам по рис. 3.1 граничными будут следующие условия:
при x = 0, |
у = 0, |
y / |
= 0 ; |
|
|
|
|
||
при x = l, |
y = 0. |
|
|
|
|
|
|
|
(3.6) |
Подставляя граничные условия (3.6) в общее решение дифференциального |
|||||||||
уравнения (3.5), получим: |
|
|
|
|
|
|
|
|
|
|
B |
- |
|
|
R |
× l |
= 0 ; |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
P |
|
|
||
A × n |
|
+ |
R |
= 0 ; |
|
||||
|
|
|
|
|
|
||||
|
P |
|
|||||||
A ×sin nl + B × cos nl |
|
|
= 0 . |
|
|||||
|
|
|
|
|
|
(3.7) |
|||
Эти уравнения имеют два решения. Первое решение – когда A = B = R = 0 .
P
Этот случай соответствует исходному (недеформированному) состоянию равновесия. Второе ненулевое решение, соответствующее деформированному
состоянию равновесия, когда A ¹ 0, B ¹ 0, R ¹ 0 . В этом случае определитель
|
|
|
P |
|
|
системы уравнений (3.7) должен быть равен нулю т.е. |
|
||||
|
1 |
-l |
|
|
|
|
0 |
|
|
||
|
n |
0 |
1 |
= 0 . |
(3.8) |
|
sin nl |
cos nl |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
В соответствии |
|
со свойством определителей, его можно разложить по |
||||||||||||||||||||||||||||||
элементам любой |
i-ой строки по формуле D = ai1 × Ai1 + ai 2 × Ai 2 |
+ . . . + ain |
× Ain , |
где |
|||||||||||||||||||||||||||||
|
= (-1)i+ j |
|
a11 . . . a1 j . . . a1n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A |
|
a |
i1 |
. . . a |
ij |
. . . a |
in |
|
|
|
- |
|
адъюнкты соответствующих элементов ( |
т.е. |
|||||||||||||||||||
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
an1 . . . anj . . . ann |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
миноры , взятые со знаком “-“ |
или “+” |
по указанной формуле). |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Раскрывая определитель (3.8) по элементам 1-ой строки, |
получим: |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
-1 |
|
|
n |
|
1 |
|
- l |
|
|
n |
0 |
|
|
= 0 , |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin nl |
0 |
|
|
|
|
sin nl |
cos nl |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или: |
sin nl - nl × cos nl = 0 , |
tg nl = nl . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Такие |
|
уравнения |
решаются |
с |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
помощью |
специальных |
таблиц |
или |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
графическим способом, как показано |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на |
рис. |
3.2. |
|
Наименьший |
корень |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения |
nl = 4,493. |
|
После |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в (3.3) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подстановки этой величины |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получаем |
|
значение |
критической |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
силы: Pкр. |
= |
20,19 |
× EI . |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3.2. Определение критической нагрузки для
однопролетных стержней энергетическим способом
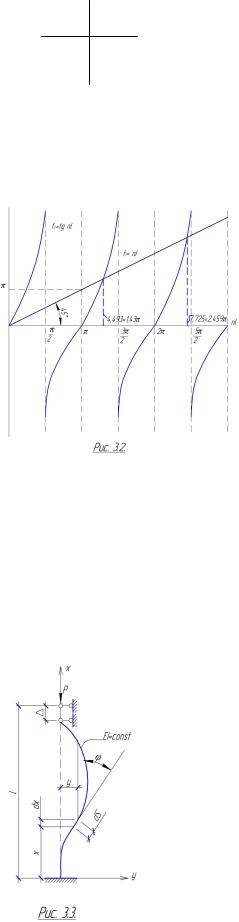
Вычислим критическую нагрузку для стержня изображенного на рис. 3.3
используя энергетический признак безразличного равновесия (1.4) δV = δA .
Приращение |
потенциальной |
энергии |
||||||||||||
деформации |
|
(учитывая, |
что |
|
M = - y // × EI ) |
|||||||||
выразится следующим образом: |
|
|
|
|
||||||||||
|
|
|
1 |
l |
M |
2 |
|
1 |
|
l |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
δV = |
∫ |
|
dx = |
× EI ∫ [y // ] |
dx |
(3.9) |
|||||||
|
EI |
|
||||||||||||
2 |
0 |
2 |
|
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
Работа |
|
внешней |
силы |
|
P |
равна |
||||||||
δA = P × D . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сближение концов стержня ( dx = ds × cos ϕ ) :
