10169

10

Статические признаки устойчивости системы

Статические признаки основаны на условиях равновесия системы в отклоненном состоянии.

Рассмотрим систему в отклоненном состоянии, близком к исходному состоянию равновесия. Если силы, удерживающие систему в отклоненном состоянии, больше заданных, то система в отклоненном состоянии не удержится,

авернется в исходное состояние. Такое равновесие называется устойчивым:

∑внутр.сил F ∑внешн.сил - устойчивое состояние равновесия.

Если силы, удерживающие систему в отклоненном состоянии, меньше

заданных, то равновесие будет неустойчивым:

∑внутр.сил P ∑внешн.сил - неустойчивое состояние равновесия.

Если силы, удерживающие систему в отклоненном состоянии, равны

заданным, то равновесие будет безразличным:

∑внутр.сил = ∑внешн.сил - безразличное состояние равновесие.

относительно опоры O . Составляя сумму моментов активных сил относительно точки O,

получим:

можно заметить, что плечо силы P, которая опрокидывает тело, возрастает, а плечо силы

Q, которая удерживает тело, уменьшается, т.е.

действующие силы удаляют систему от состояния равновесия. Равновесие неустойчивое.

Энергетические признаки устойчивости системы

Энергетический признак основан на известном принципе Дирихле, согласно которому в устойчивом состоянии равновесия потенциальная энергия системы П имеет минимальное значение по сравнению со всеми соседними положениями

11

системы, отличающимися от исходного бесконечно малыми перемещениями; в

неустойчивом состоянии равновесия – максимальное значение, а в безразличном состоянии разность двух соседних значений потенциальной энергии П равна нулю, т.е. потенциальная энергия не меняется. Этот признак можно проиллюстрировать приведенным выше примером с шариком – см. рис. 1.5. В

случае по рис. 1.5а потенциальная энергия при отклонении возрастает; в случае по рис. 1.5б – она убывает, а в случае безразличного состояния равновесия по

рис. 1.5в потенциальная энергия не изменяется.

Если записать изменение потенциальной энергии системы в форме:

В случае, если отклоненная форма равновесия системы характеризуется несколькими независимыми параметрами, то энергетический признак состояния равновесия можно представить в виде выражения экстремального значения

полной потенциальной энергии системы, т.е.:

∂П = 0 , (i = 1, 2, ..., n), ∂ i

где: П = П0 + П1 = П0 + (δV − δA) - полная потенциальная энергия системы;

П0 - потенциальная энергия в исходном недеформируемом состоянии равновесия; П1 - потенциальная энергия системы, приобретенная в отклоненном состоянии; i - обобщенная координата (параметр), определяющая положение системы в отклоненном деформированном состоянии.

12

1.2.Степень свободы системы

Числом степеней свободы системы W называют количество независимых параметров, определяющих ее положение при отклонении от положения равновесия. Изменение формы или положения системы связано с изменением координат ее характерных точек.

В зависимости от количества отклоненных форм равновесия, принимаемых стержневой системой, различают системы с конечным и бесконечным числом степеней свободы.

Конечным числом степеней свободы обладают стержневые системы,

состоящие из недеформируемых, бесконечно жестких элементов, возможные перемещения которых определяются упругими свойствами опорных закреплений.

Так, на рис. 1.7а и 1.7б показаны системы, деформации которых определяются единственным параметром – например, углом поворота ϕ . Таким образом, эти системы имеют степень свободы W = 1.

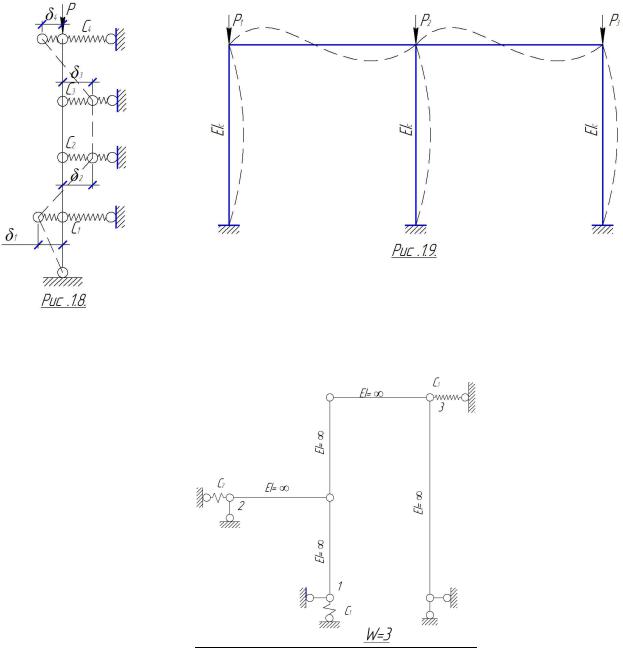
На рис. 1.8 показана система,

деформации которой определяются четырьмя независимыми параметрами

(например, перемещениями Следовательно, система имеет степень свободы W = 4.

Все системы, имеющие в своем составе

деформируемые элементы, имеют число степеней свободы, равное бесконечности. –

см. рис. 1.9.

13

Пример. Определить степень свободы системы по рис.1.10 с жесткостью

стержней EI = ∞ .

Рис. 1.10.

1.3. Устойчивость систем с конечным числом степеней свободы

Основной задачей теории устойчивости сооружений является определение критической нагрузки.

Рассмотрим стержневые системы с конечным числом степеней свободы и выразим для них значения критических нагрузок статическим или энергетическим способами. С этой целью исследуемую систему приводят в состояние

безразличного равновесия, при котором происходит потеря устойчивости, и

выражают критическую нагрузку, используя статические или энергетические признаки устойчивости.

14

Независимо от степени свободы и способа определения критической

нагрузки, расчет выполняют в следующем порядке:

-полагают, что нагрузка достигла критического значения Ркр. и система находится в состоянии безразличного равновесия;

-отклоняют систему по направлениям степеней свободы и определяют ее новое положение параметрами Di ;

-определяют реакции в упругих и неупругих связях для отклоненного состояния;

-составляют уравнения безразличного состояния равновесия в статической или энергетической формах;

-решают полученные уравнения устойчивости и определяют критическую нагрузку.

1.3.1.Определение критической нагрузки для систем с одной степенью свободы

Особенности применения статического и энергетического методов

определения критической нагрузки рассмотрим на примерах.

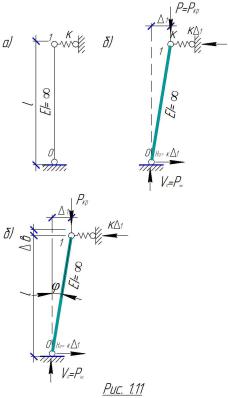
Пример 1. Определить критическую силу для стойки жесткостью EI = ∞ с абсо-

(Pкр. - K × l) × D1 = 0 .

15

Так как для отклоненного состояния D1 ¹ 0 , то сокращая параметр D1 получаем уравнение устойчивости: Pкр. - K × l = 0 .

Решая уравнение устойчивости определяем критическую силу: Pкр. = K × l (кН).

Решение энергетическим методом. Применение этого метода

предусматривает для отклоненного положения системы, находящейся в

В развернутом виде условие безразличного состояния равновесия примет вид:

Сокращая параметр D1 , получаем уравнение устойчивости K × l - Pкр. = 0 , откуда

Pкр. = K × l (кН).

1.3.2. Определение критической нагрузки для систем

снесколькими степенями свободы

Вкачестве примера рассмотрим систему с двумя степенями свободы.

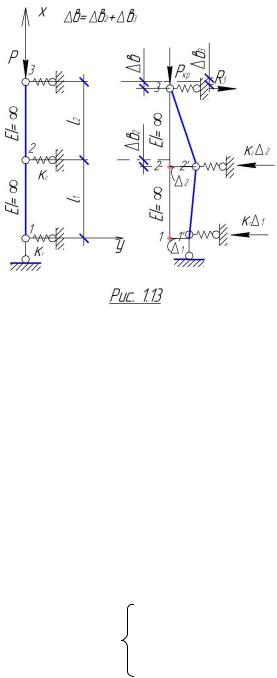
Пример: Для стойки (рис. 1.12а) с высотами участков l1 и l2 (м) ,

жесткостью EI = ∞ при абсолютно жесткой опоре 3 и упругих опорах 1 и 2 с

жесткостью K1 и K2 (кН/м) соответственно, определить критическую силу Pкр.

16

А). Решение статическим методом .

Полагаем, что P=Pкр. и стойка находится в критическом состоянии.

1.Отклоняем стойку по направлению степеней свободы на величину D1 и D2 (см. рис. 1.12б).

2.Определяем реакции в опорах:

∑ X = 0; V1 = Pкр. ; ∑Y = 0; R3 = K1 × D1 + K 2 × D2 .

3. Составляем уравнения безразличного

состояния равновесия:

∑M1 = 0; - Pкр. × D1 + R3 × (l1 + l2 ) - K 2 D2 × l1 = 0;

∑M 2верх. = 0; - Pкр. × D2 + R3 ×l2 = 0.

Сучетом значения реакции R3 (см. п. 2),

получим систему однородных уравнений:

состоянию равновесия. В этом случае должен быть равен нулю определитель системы, который и будет представлять собой уравнение устойчивости.

решая которое, определяем значение критической силы:

17

Из (3) видно, что возможны два значения критической силы. Это объясняется тем, что система с двумя степенями свободы имеет две возможные формы отклоненного (деформированного) состояния равновесия, каждой из которых соответствует свое значение критической силы. Практическое значение имеет лишь наименьшая величина критической силы. При этом формы отклоненного состояния равновесия могут быть построены из уравнений (1).

= 0,382 × K × l , так как именно этому наименьшему значению силы соответствует

P2кр. = 2,618 × K × l (см. рис. 1.12г).

Б). Решение энергетическим методом.

В состоянии равновесия потенциальная энергия системы должна иметь экстремум, т.е.

∂П = 0 , (i = 1, 2, ..., n),

¶Di

где: Di - обобщенная координата (параметр), определяющая положение системы в отклоненном деформированном состоянии;

или:

D1 × (K1 × l1 - Pкр. ) + D2 × Pкр. = 0 ;

D1 × Pкр. × l2 + D2 × (K 2 × l1 × l2 - Pкр. × l2 - Pкр. × l1 ) = 0 .

19

Pкр. × l2 (K 2 × l1 × l2 - Pкр. × l2 - Pкр. × l1 )

который и представляет собой уравнение устойчивости.

Раскрывая определитель, получаем квадратное уравнение для критической

силы:

Как видно из полученного выражения, оно полностью совпадает со значением критической силы, полученной статическим методом.

2. Устойчивость статически неопределимых систем

При расчете статически неопределимых систем, например рам,

энергетическим методом можно столкнуться с достаточно большими трудностями,

во-первых, за счет громоздкости математических выкладок, а во-вторых, при назначении формы упругих линий для многочисленных стоек и ригелей.

Последняя операция достаточно ответственна, так как неудачный выбор формы этих кривых может повлечь за собой значительную неточность определения величины критической нагрузки, причем эта неточность остается неизвестной.

Кроме того, энергетический метод расчета на устойчивость относится к приближенным методам. В то же время имеются точные методы расчета на устойчивость, которые далеко не всегда сложнее приближенных.

Для не слишком сложных статически неопределимых рам можно использовать различные методы аналогичные тем, которые применяются при обычном статическом расчете рам: метод сил, метод перемещений

(деформаций), смешанный метод и др.

Одним из наиболее широко используемых методов расчета рам на устойчивость является метод перемещений. При этом конечно в расчетах на устойчивость этот метод подвергается существенным изменениям в сравнении с его использованием для обычного статического расчета.