
9789
.pdf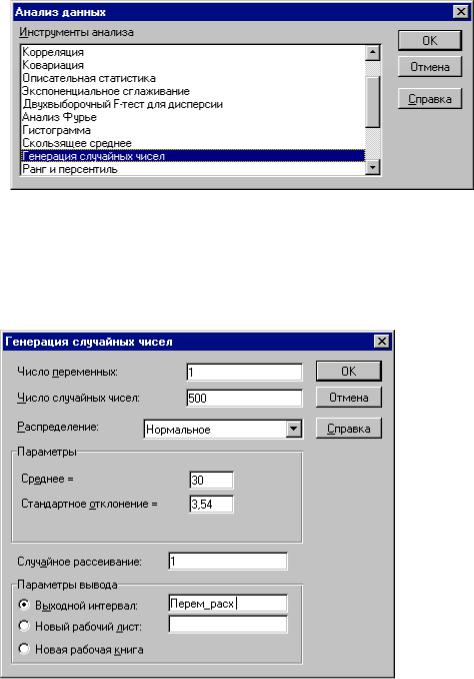
На экране появится диалоговое окно "Генерация случайных чисел". Ука-
жите в списке "Распределения" требуемый тип – "Нормальное". Заполни-
те остальные поля и нажмите кнопку "ОК". Результатом будет заполне-
ние блока ячеек А13.А512 сгенерированными случайными значениями.
Рис. Заполнение полей окна "Генерация случайных чисел"
Приведем необходимые пояснения. Первым заполняемым аргументом диалогового окна "Генерация случайных чисел" является поле "Число перемен-
ных". Оно задает количество колонок ЭТ, в которых будут размещаться сгене-
рированные в соответствии с заданным законом распределения случайные ве-
личины. В случае, если указывается число больше 1, случайные величины бу-
дут размещены в соответствующем количестве соседних колонок, начиная с ак-
101
тивной ячейки. Если это число не введено, то все колонки в выходном диапа-
зоне будут заполнены.
Следующим обязательным аргументом для заполнения является содержи-
мое поля "Число случайных чисел" (т.е. количество имитаций). При этом ППП
EXCEL автоматически подсчитывает необходимое количество ячеек для хране-
ния генеральной совокупности.
Необходимый вид распределения задается путем соответствующего выбо-
ра из списка "Распределения". Выбранный тип распределения определяет внешний вид диалогового окна. В рассматриваемом примере выбор типа рас-
пределения "Нормальное" повлек за собой появление дополнительных аргу-
ментов – его параметров "Среднее" и "Стандартное отклонение. Эти аргументы могут быть заданы только в виде констант. Использование адресов ячеек и соб-
ственных имен здесь не допускается!
Указание аргумента "Случайное рассеивание" позволяет при повторных запусках генератора получать те же значения случайных величин, что и при первом. Таким образом одну и ту же генеральную совокупность случайных чи-
сел можно получить несколько раз, что значительно повышает эффективность анализа. В случае если этот аргумент не задан (равен 0), при каждом последу-
ющем запуске генератора будет формироваться новая генеральная совокуп-
ность.
Последний аргумент диалогового окна "Генерация случайных чисел" – "Параметры вывода" определяет место расположения полученных результатов.
Место вывода задается путем установления соответствующего флажка. При этом можно выбрать три варианта размещения:
102
выходной блок ячеек на текущем листе – введите ссылку на левую верх-
нюю ячейку выходного диапазона, при этом его размер будет определен автоматически и в случае возможного наложения генерируемых значений на уже имеющиеся данные на экран будет выведено предупреждающее сообщение;
новый рабочий лист – в рабочей книге будет открыт новый лист, содер-
жащий результаты генерации случайных величин, начиная с ячейки A1;
новая рабочая книга – будет открыта новая книга с результатами имита-
ции на первом листе.
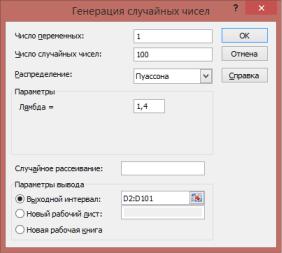
Задача 1. Получите значения 100 случайных величин, распределенных по закону Пуассона. Оцените соответствие экспериментального и теоретического распределения случайных величин.
В Excel добавим пакет «Анализ данных», с помощью функции «Генера-
ция случайных чисел» по заданным параметрам будет получено 100 случайных величин
0 |
4 |
2 |
2 |
3 |
7 |
0 |
1 |
4 |
1 |
0 |
1 |
0 |
0 |
2 |
3 |
1 |
0 |
1 |
0 |
1 |
2 |
1 |
3 |
0 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
4 |
0 |
2 |
1 |
1 |
1 |
5 |
0 |
3 |
2 |
0 |
3 |
2 |
1 |
0 |
1 |
0 |
2 |
2 |
1 |
1 |
2 |
0 |
2 |
1 |
0 |
3 |
2 |
0 |
1 |
1 |
1 |
0 |
2 |
0 |
2 |
0 |
1 |
0 |
0 |
1 |
0 |
2 |
2 |
3 |
2 |
1 |
2 |
103

1 |
2 |
1 |
0 |
2 |
0 |
2 |
0 |
0 |
3 |
2 |
2 |
1 |
2 |
1 |
1 |
0 |
0 |
2 |
1 |
Преобразуем в интервальный вариационный ряд и найдем эмпириче-
скую частоту:
Xi |
fэмп |
|
0 |
0,94086 |
28 |
0,94086 |
1,88172 |
31 |
,88172 |
2,822581 |
28 |
2,822581 |
3,763441 |
8 |
3,763441 |
4,704301 |
3 |
4,704301 |
5,645161 |
1 |
5,645161 |
6,586022 |
0 |
6,586022 |
7,526882 |
1 |
|
|
100 |
Найдем теоретическую частоту:
Шаг h=0,94, для получения эмпирической частоты используется функ-
ция в Excel:
=ЧАСТОТА(массив_данных; массив_интервалов)
fтеор |
Хсер |
|
27 |
0,47043 |
|
37 |
1,41129 |
Для определения частот теоретиче- |
25 |
2,352151 |
ского распределения Пуассона ис- |
11 |
3,293011 |
пользуется формула: |
4 |
4,233871 |
|
1 |
5,174731 |
=Целое(nhi e-λ) |
0,3 |
6,115591 |
|
0,0 |
7,056452 |
|
105,3017119
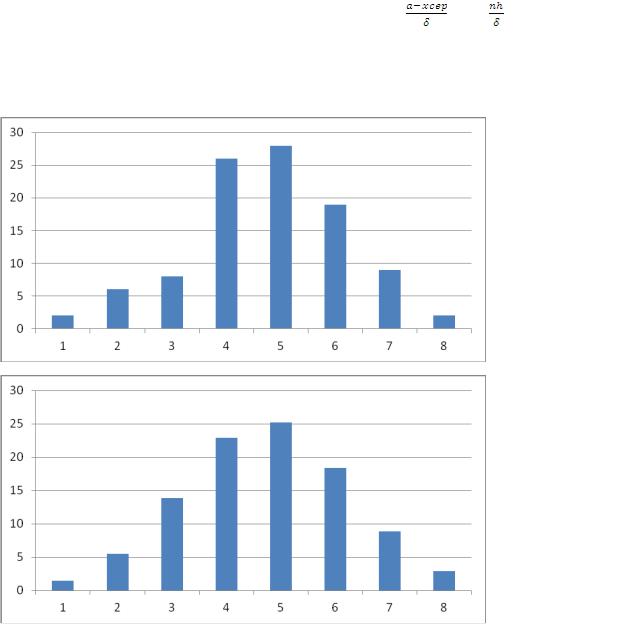
Построим гистограммы частот эмпирического и теоретического распре-
деления Пуассона:
104

Можем предположить, что данное распределение является распределе-
нием Пуассона, данную гипотезу проверяем по ХИ2 критерию:
|
|
|
|
(fэмп- |
|
|
(fэмп- |
|
|
|
Хи2расч |
|
20,95949 |
|
|
fэмп-fтеор |
|
|
fтеор)^2 |
|
|
fтеор)^2/fтеор |
|
|
|
ν |
|
6 |
|
1 |
|
1 |
0,037037037 |
|
|
|
α |
|
0,05 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
Хи2табл |
|
12,59159 |
|
-6 |
|
36 |
0,972972973 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
9 |
0,36 |
|
|
|
|
|
|
|
||||
-3 |
|
9 |
0,818181818 |
|
|
ν – кол-во степеней свободы |
||||||||
-1 |
|
1 |
0,25 |
|
|
ν = 8-1-1, единица вычитается, |
||||||||
0 |
|
0 |
0 |
|
|
т.к. один параметр λ |
||||||||
- |
|
|
|
|
|
|
|
Значение α обычно берут 0,05 |
||||||
0,252254947 |
|
0,063632558 |
0,252254947 |
|
|
|
|
|
|
|
||||
0,950543007 |
|
0,903532008 |
18,2690446 |
|
|
|
|
|
|
|
||||
|
|
|
|
Хи2 |
|
|
20,95949137 |
|
|
|
|
|
|
|
Из расчетов видно, что ХИ2расч > ХИ2табл, расхождение существенно,
следовательно, гипотеза отвергается.
Задача 2. Получите значения 100 случайных величин, распределенных по
нормальному закону распределения; постройте графики распределения плотно-
сти вероятностей; оценить соответствие экспериментального и теоретического
распределения случайных величин.
Любая сумма n нормально распределенных случайных величин дает нам
нормально распределенную случайную величину:
1)ξ = x1 + x2 + … + x12, где хi ξ (0, 1) – случайная величина равномерного распределения.
2)z = 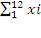 - 6 – случайное число нормального распределения , где N(0; 1).
- 6 – случайное число нормального распределения , где N(0; 1).
105

3) R = (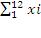 – 6)δ + a, где δ и a – заданные показатели, а R – случайное чис-
– 6)δ + a, где δ и a – заданные показатели, а R – случайное чис-
ло нормального распределения, где N(a; δ).
Таким образом, получаем 100 случайных величин, распределенных по нор-
мальному закону:
-0,4617 |
|
-1,0735 |
|
1,1544 |
|
2,3269 |
1,7836 |
1,6413 |
|
1,3869 |
1,4599 |
-1,1310 |
|
2,0073 |
||||
2,7145 |
|
-1,0618 |
|
0,0641 |
|
-1,6318 |
-2,0518 |
1,7587 |
|
1,7070 |
0,7916 |
0,3054 |
|
-1,5351 |
||||
0,4740 |
|
-2,8972 |
|
0,6228 |
|
0,0421 |
-1,1664 |
2,6478 |
|
1,4559 |
1,1223 |
-3,3992 |
|
-0,9855 |
||||
-0,8915 |
|
-1,6701 |
|
-1,9903 |
|
0,4053 |
0,2715 |
3,3035 |
|
-1,6753 |
-1,6304 |
0,3352 |
|
0,5632 |
||||
0,8607 |
|
2,8577 |
|
2,1845 |
|
-1,1538 |
-1,5079 |
2,6822 |
|
1,2370 |
2,5409 |
0,4750 |
|
-0,3094 |
||||
0,9509 |
|
0,27795 |
|
1,8405 |
|
-0,3855 |
-0,6046 |
4,6563 |
|
0,6685 |
-0,9962 |
0,9298 |
|
0,6172 |
||||
1,7622 |
|
0,28016 |
|
-2,1573 |
|
-0,9110 |
-1,7724 |
-0,4952 |
-0,1796 |
-0,1289 |
1,5728 |
|
-0,0582 |
|||||
-0,5263 |
|
0,57862 |
|
-2,0543 |
|
1,2325 |
1,5041 |
2,0423 |
|
1,0631 |
0,8359 |
2,2769 |
|
3,1301 |
||||
0,6696 |
|
-0,66416 |
|
1,2864 |
|
2,1944 |
1,5474 |
0,5351 |
|
1,4536 |
0,1571 |
-1,1529 |
|
1,5199 |
||||
0,6605 |
|
-0,13585 |
|
0,7067 |
|
3,0001 |
-0,1528 |
1,6662 |
0,2201 |
1,6587 |
-0,0638 |
0,4935 |
||||||
|
Преобразуем в интервальный вариационный ряд и найдем эмпириче- |
|||||||||||||||||
скую частоту: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
xi |
|
fэмп |
|
|
|
|
|
|
|
|
|
|
||||
|
-3,39922 |
|
-2,31649 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
-2,31649 |
|
-1,23376 |
|
11 |
|
|
Шаг h=1,083, для получения эмпири- |
|
|||||||||
|
-1,23376 |
|
-0,15103 |
|
19 |
|
|
ческой частоты используется функ- |
|
|||||||||
|
-0,15103 |
|
0,931699 |
|
30 |
|
|
ция в Excel: |
|
|
|
|
|
|||||
|
0,931699 |
|
2,014429 |
|
24 |
|
|
=ЧАСТОТА(массив_данных; мас- |
|
|||||||||
|
2,014429 |
|
3,097159 |
|
11 |
|
|
|
||||||||||
|
|
|
|
|
сив_интервалов) |
|
|
|
|
|||||||||
|
3,097159 |
|
4,179889 |
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
4,179889 |
|
5,262619 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
Найдем теоретическую частоту: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения теоретиче- |
||
|
fтеор |
|
хсер |
|
t |
|
Фи(t) |
|
|
fтеор(ц) |
|
|
|||
1,782097 |
|
-2,85786 |
|
-2,39348 |
|
0,022747 |
|
2 |
|
ской частоты нормального |
|||||
8,55096 |
|
-1,77513 |
|
-1,61004 |
|
0,109147 |
|
9 |
|
распределения используется |
|||||
22,2096 |
|
-0,6924 |
|
-0,82661 |
|
0,28349 |
|
23 |
|
формула: |
|||||
31,22546 |
|
0,390334 |
|
-0,04317 |
|
0,398571 |
|
32 |
|
f(x) = φ(t), где φ(t) – плот- |
|||||
23,76398 |
|
1,473064 |
|
0,740263 |
|
0,30333 |
|
24 |
|
|
|
|
|||
9,789753 |
|
2,555794 |
|
1,523699 |
|
0,124959 |
|
10 |
|
|
|
|
|||
|
|
|
|
|
ность распределения и φ(t) = |
|
|||||||||
2,183064 |
|
3,638524 |
|
2,307135 |
|
0,027865 |
|
3 |
|
|
|||||
|
|
|
|
|
е- , в Excel φ(t) находится |
||||||||||
0,263514 |
|
4,721254 |
|
3,090571 |
|
0,003364 |
|
1 |
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
99,76843 |
|
|
|
|
|
|
|
|
104 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по формуле |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
=НОРМРАСП(t;0;1;0). Число t |
||
|
|
|
|
|
|
|
|
|
106 |
|
|
|
|
|
|
= |
. |
= 78,344 |
Построим гистограммы частот эмпирического и теоретического нор-
мального распределения соответственно:
Можем предположить, что данное распределение является нормальным распределением, данную гипотезу проверяем по ХИ2 критерию:
|
|
|
|
(fэмп- |
|
|
(fэмп- |
|
|
Хи2расч |
1,69843 |
|
|
fэмп-fтеор |
|
|
fтеор)^2 |
|
|
fтеор)^2/fтеор |
|
|
V |
5 |
|
0 |
|
|
0 |
0 |
|
|
alpha |
0,05 |
|
|||
2 |
|
|
4 |
0,444444444 |
|
|
Хи2табл |
11,0705 |
|
|||
-4 |
|
|
16 |
0,695652174 |
|
|
|
|
|
|||
-2 |
|
|
4 |
0,125 |
|
ν – кол-во степеней свободы |
||||||
0 |
|
|
0 |
0 |
|
|||||||
|
|
|
ν = 8-1-2, две единицы вычи- |
|||||||||
1 |
|
|
1 |
0,1 |
|
|||||||
|
|
|
тается, т.к. два параметра δ и |
|||||||||
-1 |
|
|
1 |
0,333333333 |
|
|||||||
|
|
|
Мх |
|
|
|||||||
0 |
|
|
0 |
0 |
|
|
|
|||||
|
|
|
Значение α обычно берут 0,05 |
|||||||||
|
|
|
|
Хи2 |
|
|
1,698429952 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
107 |
|
|
|
|
|
|
Проведем имитационный эксперимент: |
|
|||||
|
|
|
|
|
|
|
№ |
|
Хи2 |
|
|
|
|
1 |
|
1,69843 |
|
|
|
|
2 |
|
15,47706 |
|
|
|
|
3 |
|
0,908333 |
|
|
С помощью имитационного экспе- |
|
4 |
|
3,947038 |
|
|
||
|
|
|
римента генерируем 100 значений, |
|||
5 |
|
10,71309 |
|
|
||
|
|
|
которые может принимать ХИ2 и |
|||
6 |
|
6,455872 |
|
|
||
|
|
|
находим среднее из них. Его сравни- |
|||
7 |
|
6,419028 |
|
|
||
|
|
|
ваем с ХИ табличным и получаем: |
|||
…………………….. |
||||||
|
||||||
|
|
|
|
|
6,294413 < 11,0705, т.о. |
|
96 |
|
2,067432 |
|
|
||
97 |
|
4,735238 |
|
|
ХИ2расч < ХИ2табл, расхождение не |
|
98 |
|
4,828134 |
|
|
||
|
|
|
существенно, следовательно, гипоте- |
|||
99 |
|
6,913078 |
|
|
||
|
|
|
за принимается. |
|||
100 |
|
2,748333 |
|
|
||
|
|
|
|
|||
|
|
6,294413 |
|
|
|
|
Задачи для раздела 6. Дискретно-событийное моделирование.
Задача 1. Покупатели подходят к кассе супермаркета с интенсивностью,
которая приведена в таблице ниже:
Интервал (мин): |
1 |
2 |
|
3 |
4 |
5 |
Процент: |
40% |
30% |
10% |
10% |
|
10% |
Обычно на обслуживание одного покупателя уходит две минуты. Смо-
делируйте подход первых 20 клиентов к кассе и определите длину очереди при
подходе каждого из них.
Решение.
Для моделирования последовательного прибытия клиентов будем исполь-
зовать случайные числа. Так, если взять случайные двузначные числа, то пер-
вые 40 чисел (00—39) покажут интервал в 1 минуту. Следующие 30 случайных
чисел (40—69) покажут интервал в 2 минуты и т. д. (см. таблицу ниже):
Интервал между |
последователь- |
1 |
2 |
3 |
4 |
|
|
ным прибытием клиентов (мин) |
5 |
||||||
|
|
|
|
||||
Процент клиентов |
|
40% |
30% |
10% |
10% |
10% |
|
|
|
||||||
|
|
|
|
|
|
|
|
Случайные числа |
|
0-39 |
40-69 |
70-79 |
80-89 |
90-99 |
|
|
|
||||||
|
|
|
|
|
|
|
|
108

Смоделируем интервалы последовательного прибытия клиентов. Мы ис-
ходим из того, что отсчет начинается с 0, и видно, что первый клиент прибыва-
ет одной минутой позже. Второй клиент прибывает с интервалом в 2 минуты,
то есть он прибывает на третьей минуте. В принципе, фактическое время при-
бытия любого клиента получается путем прибавления временного интервала по клиенту ко времени прибытия предшествующего клиента. Как видно из модели,
двадцать клиентов прибыли в первые тридцать пять минут.
|
|
|
|
|
|
|
|
|
|
Время |
окон- |
|
случайные |
интервал |
Время |
|
Время обслу- |
Длина |
Время |
Время начала |
чания |
обслу- |
|
Клиент |
числа |
прибытия |
прибытия |
живания |
|
очереди |
ожидания |
обслуживания |
живания |
||
1 |
22 |
1 |
|
1 |
|
2 |
0 |
0 |
1 |
3 |
|
|
|
|
|
||||||||
2 |
65 |
2 |
|
3 |
|
2 |
0 |
0 |
3 |
5 |
|
|
|
|
|
||||||||
3 |
67 |
2 |
|
5 |
|
2 |
0 |
0 |
5 |
7 |
|
|
|
|
|
||||||||
4 |
74 |
3 |
|
8 |
|
2 |
0 |
0 |
8 |
10 |
|
|
|
|
|
||||||||
5 |
15 |
1 |
|
9 |
|
2 |
1 |
1 |
10 |
12 |
|
|
|
|
|
||||||||
6 |
21 |
1 |
|
10 |
|
2 |
1 |
2 |
12 |
14 |
|
|
|
|
|
||||||||
7 |
69 |
2 |
|
12 |
|
2 |
1 |
2 |
14 |
16 |
|
|
|
|
|
||||||||
8 |
2 |
1 |
|
13 |
|
2 |
2 |
3 |
16 |
18 |
|
|
|
|
|
||||||||
9 |
39 |
1 |
|
14 |
|
2 |
2 |
4 |
18 |
20 |
|
|
|
|
|
||||||||
10 |
98 |
5 |
|
19 |
|
2 |
1 |
1 |
20 |
22 |
|
|
|
|
|
||||||||
11 |
5 |
1 |
|
20 |
|
2 |
1 |
2 |
22 |
24 |
|
|
|
|
|
||||||||
12 |
30 |
1 |
|
21 |
|
2 |
2 |
3 |
24 |
26 |
|
|
|
|
|
||||||||
13 |
3 |
1 |
|
22 |
|
2 |
1 |
4 |
26 |
28 |
|
|
|
|
|
||||||||
14 |
50 |
2 |
|
24 |
|
2 |
2 |
4 |
28 |
30 |
|
|
|
|
|
||||||||
15 |
31 |
1 |
|
25 |
|
2 |
2 |
5 |
30 |
32 |
|
|
|
|
|
||||||||
16 |
2 |
1 |
|
26 |
|
2 |
3 |
6 |
32 |
34 |
|
|
|
|
|
||||||||
17 |
97 |
5 |
|
31 |
|
2 |
2 |
3 |
34 |
36 |
|
|
|
|
|
||||||||
18 |
1 |
1 |
|
32 |
|
2 |
2 |
4 |
36 |
38 |
|
|
|
|
|
||||||||
19 |
16 |
1 |
|
33 |
|
2 |
3 |
5 |
38 |
40 |
|
|
|
|
|
||||||||
20 |
59 |
2 |
|
35 |
|
2 |
3 |
5 |
40 |
42 |
|
|
|
|
|
||||||||
Из модели видно, что время ожидания клиента со времени начала работы
109

кассы увеличивается. |
|
|
|
|
|
|
|||||
|
Определим |
абсолютную |
пропускную |
способность |
магазина: |
||||||
А |
Nоб |
|
17 |
60 24,29 человек в час. |
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
Тсист |
42 |
|
|
|
|
|
|
|
|
|
|
Задача 2. Рассмотрите задачу 1, если фактическое время обслуживания |
||||||||||
покупателей различно и распределяется следующим образом: |
|
||||||||||
|
Время обслуживания (мин): |
1 |
2 |
3 |
4 |
5 |
|
||||
|
Процент: |
|
0 |
20 |
30 |
35 |
5 |
|
|||
Смоделируйте подход первых 20 покупателей и определите среднюю длину очереди и среднее время ожидания для каждого из них.
Решение.
Время обслуживания можно смоделировать с помощью двузначных чисел,
как мы это делали ранее. Так, первые 10 случайных чисел (00—09) показывают время обслуживания в 1 минуты. Далее в таблице приведены случайные числа,
которые отражают определенное время обслуживания:
|
|
Время обслуживания (мин) |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Случайные числа |
|
|
0-09 |
|
10-29 |
|
30-59 |
|
60-94 |
|
95-99 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Время |
|
|
|
|
|
|
|
|
|
Время |
|
|
|
|
|
|
Время начала |
окончан |
||
|
|
случайные |
интервал |
Время |
|
случай- |
обслужи- |
Длина |
Время |
ожи- |
обслужива- |
обслуж |
|||||||
Клиент |
числа |
|
прибытия |
прибытия |
ные числа |
вания |
очереди |
дания |
|
|
ния |
|
ния |
||||||
1 |
|
52 |
2 |
|
2 |
51 |
3 |
0 |
0 |
|
2 |
|
5 |
||||||
2 |
|
93 |
5 |
|
7 |
90 |
4 |
0 |
0 |
|
|
7 |
|
11 |
|||||
3 |
|
84 |
4 |
|
11 |
81 |
4 |
0 |
0 |
|
|
11 |
|
15 |
|||||
4 |
|
1 |
1 |
|
12 |
40 |
3 |
1 |
3 |
|
|
15 |
|
18 |
|||||
5 |
|
38 |
1 |
|
13 |
91 |
4 |
2 |
5 |
|
|
18 |
|
22 |
|||||
6 |
|
94 |
5 |
|
18 |
78 |
4 |
1 |
4 |
|
|
22 |
|
26 |
|||||
7 |
|
28 |
1 |
|
19 |
45 |
3 |
2 |
7 |
|
|
26 |
|
29 |
|||||
8 |
|
8 |
1 |
|
20 |
17 |
2 |
3 |
9 |
|
|
29 |
|
31 |
|||||
9 |
|
68 |
2 |
|
22 |
90 |
4 |
3 |
9 |
|
|
31 |
|
35 |
|||||
10 |
|
27 |
1 |
|
23 |
11 |
2 |
4 |
12 |
|
|
35 |
|
37 |
|||||
11 |
|
37 |
1 |
|
24 |
99 |
5 |
5 |
13 |
|
|
37 |
|
42 |
|||||
12 |
|
48 |
2 |
|
26 |
28 |
2 |
5 |
16 |
|
|
42 |
|
44 |
|||||
13 |
|
63 |
2 |
|
28 |
63 |
4 |
6 |
16 |
|
|
44 |
|
48 |
|||||
14 |
|
88 |
4 |
|
32 |
31 |
3 |
5 |
16 |
|
|
48 |
|
51 |
|||||
15 |
|
98 |
5 |
|
37 |
1 |
1 |
4 |
14 |
|
|
51 |
|
52 |
|||||
110
