9758

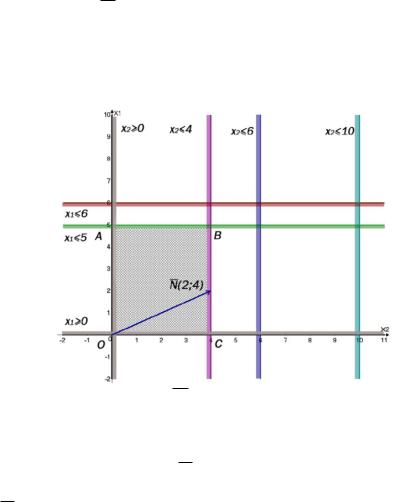
Находим координаты вершин области (х1;х2).

Для точки А координаты вершины (5;0); для точки В координаты вершины

(5;4); для точки С координаты вершины (0;4); координаты точки О(0;0) совпа-

дают с началом координат.

Целевая функция Z 2x1 4x2 max определяет на плоскости семейство параллельных прямых, каждой из которых соответствует определенное значе-

ние.

Вектор N (2;4) с координатами с1=1, с2=4 и выходящий из начала коорди-

нат, перпендикулярный к этим прямым, указывает направление наискорейшего возрастания функции, а противоположный вектор – направление убывания.

Рис.9. Вектор

Для определения Zmax построим линию уровня Z 2х1 4х2 0 , перпен-

дикулярную вектору N (2;4) , и будем передвигать ее в направлении вектора

N (2;4) до тех пор, пока она не коснется последней крайней (угловой) точки многоугольника решений. Координаты этой точки и определяет Zmax .

121

Рис. 10. Графическое нахождение fmax

Из рисунка 10 видно, что Zmax находится в точке В(5;4).

Zmax 2x1 4x2 2 5 4 4 26

Ответ: Максимальная прибыль предприятия 26 тыс. условных единиц в год, для получения такой прибыли предприятие должно выпустить 5 тыс. дета-

лей вида 1 и 4 тыс. деталей вида 2.

3. Симплекс-метод.

х1 6; х2 6;х2 4;х1 5; х2 10;

х1, х2 0

Z 2x1 4x2 max

Запишем задачу в канонической форме, т.е. ограничения-неравенства пе-

репишем в виде равенств, добавляя балансовые переменные:

Z 2x1 4x2 0

122

х1, х2 0

Эта система является системой с базисом (базис s1, s2, s3, s4, s5, каждая из них входит только в одно уравнение системы с коэффициентом 1), x1 и x2 – сво-

бодные переменные. Задачи, при решении которых применяется симплекс-

метод, должны обладать следующими двумя свойствами:

–система ограничений должна быть системой уравнений с базисом;

–свободные члены всех уравнений в системе должны быть неотрицатель-

ны.

Полученная система – система с базисом и ее свободные члены неотрица-

тельны, поэтому можно применить симплекс-метод. Составим первую сим-

плекс-таблицу (Таблица 1) для решения задачи на симплекс-метод, т.е. табли-

цу коэффициентов целевой функции и системы уравнений при соответствую-

щих переменных. Здесь «БП» означает столбец базисных переменных, «Реше-

ние» – столбец правых частей уравнений системы. Решение не является опти-

мальным, т.к. в z – строке есть отрицательные коэффициенты.

Таблица 1

Для улучшения решения перейдем к следующей симплекс-таблице (табли-

ца 2). Для этого надо в таблице 1 выбрать разрешающий столбец, т.е. пере-

менную, которая войдет в базис на следующей итерации симплекс-метода. Он выбирается по наибольшему по модулю отрицательному коэффициенту в z-

строке (в задаче на максимум) – в начальной итерации симплекс-метода это столбец x2 (коэффициент -4).

Затем выбирается разрешающая строка, т.е. переменная, которая выйдет из базиса на следующей итерации симплекс-метода. Она выбирается по наименьшему отношению столбца "Решение" к соответствующим положитель-

ным элементам разрешающего столбца (столбец «Отношение») – в начальной итерации это строка s3 (коэффициент 4).

Разрешающий элемент находится на пересечении разрешающего столбца и разрешающей строки, его ячейка выделена цветом, он равен 1. Следователь-

но, на следующей итерации симплекс-метода переменная x2 заменит в базисе s1.

Заметим, что в z-строке отношение не ищется, там ставится прочерк " - ". В

случае если есть одинаковые минимальные отношения, то выбирается любое из них. Если в разрешающем столбце все коэффициенты меньше или равны 0, то решение задачи бесконечно.

Заполняем таблицу 2.

1) Вычисление строки х2 таблицы 2. Сначала делим все члены разрешаю-

щей строки s3 таблицы 1 на разрешающий элемент (он равен 1 в данном случае)

этой таблицы, получим строку x2 в таблице 2. Т.к. разрешающий элемент в дан-

ном случае равен 1, то строка s3 таблицы 1 будет совпадать со строкой х2 таб-

лицы 2. Строку x2 таблицы 2 мы получили 0 1 0 0 1 20, остальные строки таб-

лицы 2 будут получены из этой строки и строк таблицы 1 следующим образом:

2)Вычисление z-строки таблицы 2. На месте -4 в первой строке (z-строке)

встолбце х2 таблицы 1 должен быть 0 в первой строке таблицы 2. Для этого все элементы строки х2 таблицы 2 (0 1 0 0 1 0 0 4) умножим на 4, получим (0 4 0 0 4

0 0 16) и сложим эту строку с первой строкой (z - строкой) таблицы 1 (-2 -4 0 0 124

0 0 0 0), получим (-2 0 0 0 4 0 0 16). В столбце x2 появился ноль 0, цель достиг-

нута. Элементы разрешающего столбца х2 выделены красным цветом.

3)Строку s1 оставляем без изменений.

4)Вычисление строки s2 таблицы 2. На месте 1 в s2 строке таблицы 1 дол-

жен быть 0 в таблице 2. Для этого все элементы строки х2 таблицы 2 (0 1 0 0 1 0

0 4) умножим на -1, получим 0 -1 0 0 -1 0 0 -4 и сложим эту строку с s2 - стро-

кой таблицы 1 (0 1 0 1 0 0 0 6), получим строку (0 0 0 1 -1 0 0 2). В столбце х2

получен необходимый 0.

5) Вычисление строки s5 таблицы 2. На месте 1 в s5 строке таблицы 1 дол-

жен быть 0 в таблице 2. Для этого все элементы строки х2 таблицы 2 (0 1 0 0 1 0

0 4) умножим на -1, получим 0 -1 0 0 -1 0 0 -4 и сложим эту строку с s5 - стро-

кой таблицы 1 (0 1 0 0 0 0 1 10), получим строку 0 0 0 0 -1 0 1 6. В столбце х2

получен нужный 0. Столбец х2 в таблице 2 стал единичным, он содержит одну 1

и остальные 0.

Разрешающий столбец х1, разрешающая строка s4, s4 выходит из базиса, х1

входит в базис (таблица 3).

В z-строке все коэффициенты неотрицательны, следовательно, получено оптимальное решение x1 = 5, x2 = 4, zmax = 26.

Ответ: Максимальная прибыль предприятия 26 тыс. условных единиц в год, для получения такой прибыли предприятие должно выпустить 5 тыс. дета-

лей вида 1 и 4 тыс. деталей вида 2.

Задача 6. (Пример решения прямой и двойственной задачи).

Пусть в производстве 4-х видов продукции участвуют 4 вида ресурсов. Из-

вестны нормы расхода ресурсов на производство единицы продукции (матрица А), цены ее реализации (матрица С) и запасы ресурсов (матрица В). Определить план производства продукции, максимизирующий выручку от реализации про-

изведенной продукции.

Тогда математическая модель задачи примет вид: найти х1, х2, х3, х4 (объе-

мы производства каждого вида продукции), удовлетворяющие ограничениям:

при которых функция z=4x1+5x2+7x3+9x4 достигает максимума.

126

При решении задачи симплексным методом она приводится к канониче-

скому виду добавлением в левые части ограничений неотрицательных балансо-

вых переменных:

z 4x1 5x2 7x3 9x4 max .

Ответ: для получения максимального дохода от реализации производ-

ственной продукции ее необходимо выпустить в объемах: х1*=67,083; х2*=0;

х3*=15; х4*=103,333. При этом zmax=1303,333.

Двойственная задача. Найти значения переменных у1, у2 у3, у4, удовлетво-

ряющих ограничениям:

w=550y1+400y2+650y3+520y4

Решения этой задачи выпишем из последнего столбца таблицы y1*=0,833, y2*=0, y3*=1,167, y4*=0,167.

Проиллюстрируем свойства двойственных оценок на основе этой задачи. 1. Каждая из оценок указывает, на сколько изменится максимальное значе-

ние целевой функции (максимальная выручка), если изменить на единицу запа-

сы соответствующих ресурсов. Наибольшее изменение выручки произойдет,

если изменить объем 3-го ресурса ( y3* =1,167), а изменение второго ресурса (в

границах устойчивости) не приведет к изменению целевой функции (у2*=0).

2. Оценки у1*, у3*, у4* положительны. Это означает, что при реализации оп-

тимального плана соответствующие ресурсы расходуются полностью. Прове-

127

рим это. Подставим x j* в 1-е сопряженные условия исходной задачи.

4 67,083 2 0 5 15 2 103,333 549,999 550 .

Аналогично для третьего и четвертого ресурсов (проверить самостоятель-

но). Следовательно, 1, 3, 4-й ресурсы дефицитны. у2*=0. Это означает, что в оп-

тимальном решении второй ресурс расходуется не полностью. Проверим это.

Подставим x j во второе ограничение исходной задачи:

3 67,083 315 103,333 349,582 400.

Остаток второго ресурса составляет 400–349б582 50,4. Это и есть значе-

ние балансовой переменной в оптимальном решении исходной задачи.

4. Рентабельными являются 1-я, 3-я и 4-я продукции (х1*, х2*, х3* в оптимальном плане положительны), а нерентабельной 2-я – х2*. Проверим это, подставив уi* в

2 0,833 5 1,167 0,167 7,668 5 .

Итак, оценка ресурсов, необходимых для производства единицы 2-й про-

дукции больше цены единицы этой продукции на 7,668–5=2,668.

Задача 6. (решение целочисленной задачи методом Гомори)

Целочисленная задача линейного программирования задана следующей математической моделью:

z 3x1 x2 max ; 2x1 3x2 6;

2x1 3x2 3

128

x1, x2 x1, x2 0

Решение.

Сначала решаем задачу симплекс-методом без ограничений целочисленно-

сти. Приводим задачу к каноническому виду: z 3x1 x2 max

2x1 3x2 х3 6 2x1 3x2 х4 3

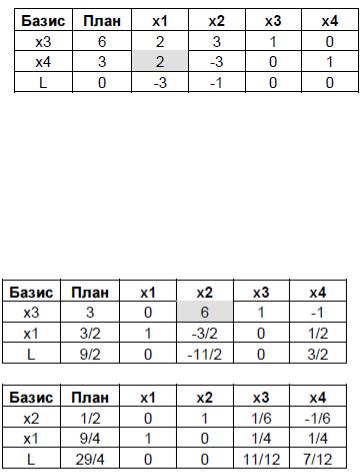
Строим симплекс-таблицу:

В последней оценочной строке есть отрицательные оценки, поэтому нужно делать шаг симплекс-метода. Выбираем столбец с наименьшей оценкой ( x1 ), а

затем разрешающий элемент по наименьшему отношению свободных членов к коэффициентам столбца ( x4 ). Результат шага запишем в таблицу (разрешаю-

щий элемент будем выделять серым). Аналогично будем повторять шаги.

В последней строке нет отрицательных оценок, поэтому оптимальное ре-

шение найдено: x1 = 9 / 4 , x2 =1/ 2 , max L = 29 / 4 .

Продолжим решение, используя алгоритм Гомори.

129

Выбираем переменную с наибольшей дробной частью, то есть x2 (дробная часть 1/2).

Вводим дополнительное ограничение целочисленности:

Добавляем это ограничение к симплекс-таблице и получаем:

Переходим к следующей таблице:

Получили нецелочисленное решение.

Выбираем переменную с наибольшей дробной частью, то есть x2 (дробная часть 3/5).

Вводим дополнительное ограничение целочисленности:

Добавляем это ограничение к симплекс-таблице и получаем:

130