8781

61

Таким образом, при любом процессе в разреженном газе начальные и конечные параметрами связаны равенством (1.5), а поскольку конечное состояние выбрано произвольно, можно заключить, что при любом состоянии

разреженного газа произведение давления на объем, деленное на абсолютную температуру, для данной массы газа есть величина постоянная:

T

Значение постоянной B зависит от массы и рода газа. Из формулы (1.6) следует, что

pV=BT.

Это выражение является уравнением состояния идеального газа и часто называется формулой Клайперона - Менделеева.

Замечание к процедуре вывода уравнения состояния При получении окончательного выражения мы рассмотрели конкретный

термодинамический процесс, состоящий из двух изопроцессов. Результат не изменится, если рассмотреть любой другой путь, состоящий из двух изопроцессов (p1 → p2 при V=const + V1 → V2 при p=const, или T1 → T2 при V=const +V1 → V2 при T=const и т. п.). Рекомендуем вам в качестве полезного упражнения доказать, что результат не зависит от пути, который рассматривается.

Универсальная газовая постоянная. В соответствии с законом,

установленным Авогадро, моли всех газов занимают при одинаковых условиях (т.е. при одинаковых температуре и давлении) одинаковый объем - Vμ . В

частности, при так называемых нормальных условиях (н.у.), т.е. при температуре 00 C и давлении 1атм (1,01×105 Па ), объем моля любого газа Vμ =22,4л/моль= 22,4 ×10−3 м3 / моль. Это позволяет при помощи формулы (1.6)

найти константу B для одного моля газа, которая обозначается R:

Важно, что согласно закону Авогадро, величина R будет одной и той же для любого газа, поэтому ее называют универсальной газовой постоянной.От уравнения (1.7), записанного для одного моля газа

рVμ =RT, (1.9)

легко перейти к уравнению для любой массы газа m. Если один моль газа имеет объем Vμ , то ν молей при тех же условиях будут иметь объем в ν раз больший:

V=νVμ , т.е. Vμ =V/ν. Подставляя это равенство в формулу (1.7), получим:

64

1)Газ сильно разрежен, так что собственный объем молекул газа Vмол Nаm/μ V1 существенно меньше объема сосуда, в котором находится газ (Vмол. < V).

2)Силами взаимодействия между молекулами такого разреженного газа можно пренебречь и учитывать взаимодействие только при столкновении молекул.

3)Столкновения молекул газа между собой и со стенками сосуда являются абсолютно упругими (молекулы - упругие шарики).

4)Молекулы газа совершают беспорядочное тепловое движение, т.е. направления скоростей ориентированы в пространстве совершенно беспорядочно. Это означает, что в каждом направлении в данный момент движется одинаковое число молекул, т.е. N/6, где N - полное число молекул газа (N/3 молекул движется параллельно каждой из осей координат, причем половина из них движется в положительном направлении, а другая - в противоположную сторону).

Давление молекул на стенку сосуда. Давление согласно

определению равно силе, с которой газ воздействует на площадку единичной площади, перпендикулярно площадке:

p = F , S

где S - площадь плоской площадки, например стенки сосуда.Величина суммарной силы воздействия молекул на площадку по III закону Ньютона равна суммарной силе, действующей на систему молекул со стороны площадки. Следовательно, сила может быть найдена по II закону Ньютона для системы материальных точек:

молекул N', которые ударяются о площадку за малое время t, и, во-вторых, изменение импульса каждой молекулы.

Если молекула массы m0 налетает в направлении, перпендикулярном площадке, со скоростью υ, то в результате абсолютно упругого удара с тяжелой площадкой (масса сосуда много больше массы молекулы) молекула отскочит с такой же скоростью в противоположном направлении (это известно из механики). То есть изменение импульса одной молекулы равно:

P1 = m0υ − (−m0υ) = 2m0υ .

Теперь необходимо вычислить число молекул N'. Сколько молекул столкнутся с площадкой за время t? Это будут все молекулы, расположенные

65

в объеме V и летящие в направлении, перпендикулярном площадке. Значит, это составит 1/6 от всех молекул, содержащихся в объеме V:

N ¢ = 1 nDV ,

6

где n - концентрация молекул газа, т.е. число молекул в единице объема.

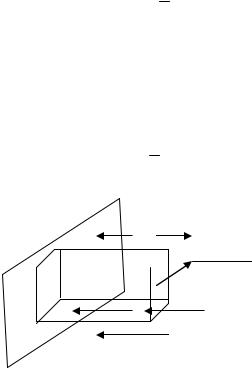
Чем определяется объем V? Это тот объем, из которого молекулы, движущиеся в сторону площадки, успевают ее достичь за время t (см. рис.1.6). Значит, высота равна υΔt, а основание - S, что позволяет определить V= S υΔt и записать выражение для числа столкновений:

N ¢ = 1 nDSυDt .

6

υΔt S

Рис. 1.6. Объем V, из которого молекулы достигают площадки за время t

Таким образом, мы получили формулу:

Это есть основное уравнение молекулярно-кинетической теории идеального газа,} которое означает:

давление в газе пропорционально средней энергии теплового движения молекул и числу молекул в единице объема.

1.6. Замечание о средней квадратичной скорости. Распределение Максвелла молекул по скоростям

66

Выше мы говорили о средней энергии теплового движения молекул. Дело в том, что молекулы движутся неупорядоченно, т.е. их скорости имеют не только случайные направления, но и величину. Спрашивается: какой смысл имеет величина υ2, если разные молекулы имеют разные значения скорости?

Если газ содержит N молекул и занимает объем V, то концентрация молекул равна n=N/V. Предположим, что N1 молекул имеют величину скорости, равную υ1, N2 молекул - скорость υ2 …N k молекул - значение скорости υk. Естественно, что N1 + N2 + … +Nk =N. В таком случае число молекул первой

Таким образом, при упрощенном выводе формулы (1.12) мы заменили реальные скорости частиц некоторой средней скоростью, которая согласно только что полученной формуле является средней квадратичной скоростью, квадрат которой равен среднему арифметическому квадратов скоростей всех молекул газа. В частности, если имеется только 2 молекулы, движущиеся со скоростями υ1 и υ2 (k=2, N1=N2=1, N=2), υ2=(υ21+υ22)/2.

Средняя энергия теплового движения молекул равна кинетической

энергии молекулы, движущейся со средней квадратичной скоростью.

В действительности молекулы могут иметь не дискретные, а непрерывные

значения скоростей. Следовательно, в реальности число групп k молекул,

имеющих разные скорости, бесконечно велико k→∞. В этом случае

69

С другой стороны, величины m0υ2x/2, m0υ2y/2, m0υ2z/2 представляют собой энергию поступательного движения вдоль каждой из трех осей координат или энергию, приходящуюся на одну степень свободы.

Числом степеней свободы называется число независимых координат,

которые необходимо задать для определения положения тела в пространстве.

Положение материальной точки в пространстве определяется тремя координатами - 3 степени свободы. Для того, чтобы задать положение гантельки (т.е. тела, состоящего из двух жестко связанных материальных точек), необходимо задать положение ее центра масс (три координаты) и еще два угла, которые составляет ось гантельки с двумя из осей координат (угол с третьей осью координат не является независимым) - 5 степеней свободы. В общем случае несимметричное твердое тело имеет 6 степеней свободы.

В случае поступательного движения молекул газа, как мы уяснили, на каждую степень свободы приходится 1/3 общей энергии молекулы, т.е.

ε 0 = 1 kT .

2

Если молекула состоит из двух и более атомов, полное число степеней свободы i увеличивается:

i=iпост+iвр.

При этом в тепловом равновесии на каждую степень свободы по- прежнему будет приходиться энергияε0 . Таким образом, с учетом возможности вращательного движения сложных молекул средняя энергия ε движения одной молекулы равна:

Из сказанного ясно, что энергия движения двухатомных молекул равна 5kT/2 (iвр=2), а трех и более атомных молекул - 3kT (iвр=3).

Внутренняя энергия идеального газа. Как уже говорилось, расстояние между молекулами газа при нормальных условиях примерно в 10 раз больше характерного размера молекул. Это означает, что молекулы находятся далеко друг от друга и силой взаимодействия между ними, а следовательно энергией их взаимодействия, можно пренебречь. Именно такая модель невзаимодействующих молекул соответствует идеальному газу.

Внутренняя энергия идеального газа представляет собой суммарную

кинетическую энергию всех молекул данной массы газа.

Средняя кинетическая энергия одной молекулы равна <ε0>=ikT/2, где i - число степеней свободы:

i=3 - для газов, молекулы которых состоят из одного атома и не имеют вращательных степеней свободы (это имеет место для всех инертных газов, например He;

i=5 - для O2, N2, H2 и большинства других простых газов, имеющих двухатомные молекулы;

70

i=6 - для CO2, паров воды H2O) и других газов, имеющих трех-и более атомные молекулы.

Поскольку в одном моле газа содержится Nа молекул, внутренняя энергия одного моля газа равна:

Если масса газа равна m, это составляет n=m/m молей. Следовательно, внутреняя энергия Um массы m газа определится формулой:

Важно! Внутренняя энергия идеального газа зависит только от температуры и не меняется при изменении объема и давления (если при этом

T=const).

В случае других веществ и реальных газов (сжатые до p=100 атм. и более при комнатной температуре газы) ситуация другая. Поскольку концентрация молекул n=p/(kT) возрастает с ростом давления, то объем V1=1/n, приходящийся на одну молекулу, становится сравнимым с объемом самой молекулы. Молекулы сильно сближаются и становится существенной энергия взаимодействия между ними (потенциальная энергия). В этих условиях внутренняя энергия будет зависеть и от расстояния между молекулами, т.е. от объема газа.

1.8. Примеры решения задач

Задача 1

Найти число молекул в 1 см3 газа, находящегося при t=27оC под давлением

10-12 атм.

Определить внутреннюю энергию а)водорода (H2), б)гелия (He), в)углекислого газа (CO2) находящегося в 1см3 в состоянии, соответствующем предыдущей задаче.

Решение:

Заметим, что число молекул N в заданном объеме, полученное в предыдущей задаче, не зависит от вида газа.