8781

191

частот. Этот результат парадоксальный, поскольку тело не имеет бесконечной энергии. Эта особенность классической теории теплового излучения была названа ультрафиолетовой катастрофой, поскольку подрывала все устои физики.

Формула планка*

Тупиковую ситуацию разрешил в 1890 г. немецкий физик-теоретик Макс Планк, предположивший, что электромагнитные колебания излучаются атомами не непрерывно, а дискретными порциями (квантами), энергия которых ε пропорциональна частоте ν

n=0

Заметим что средняя энергия равна kT только для малых частот. Для больших частот эта величина экспоненциально уменьшается. Теперь, заменяя в формуле (7) kT выражение средней энергии, полученной в (9) для величины uν будем иметь :

Это известная формула Планка, которая даёт корректный спектр теплового излучения. Для излучательной способности абсолютно чёрного тела получаются соотношения:

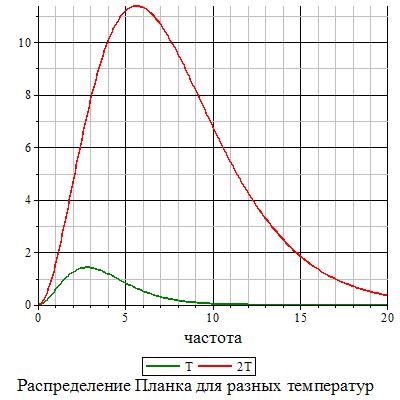
Графики первой из двух функций приведены на рисунке для двух температур, отличающихся в два раза (единицы измерения по осям условные).

192

Закон Стефана – Больцмана. Законы Вина.

Из рисунка видно, что спектр абсолютно черного тела всегда является сплошным, то есть в спектре представлен непрерывный ряд длин волн.

Поскольку энергетическая светимость АЧТ

Rэ = ∞∫ rλdλ, площадь под кривой Кирхгофа пропорциональна излучательной

0

способности АЧТ. С увеличением температуры излучательная способность АЧТ растет. Закон Стефана – Больцмана: энергетическая светимость абсолютно черного тела

пропорциональна четвертой степени его термодинамической температуры

э

где σ = 5,67 ×10−8 Вт× м−2К−4 – постоянная Стефана-Больцмана.

Для реальных тепловых излучателей Rэ = kσТ4 , где k – коэффициент серости.

Закон (11) был получен экспериментально ранее формулы Планка.

Интегрированием распределения Планка, можно получить этот закон, а кроме того показать, что постоянная Стефана-Больцмана выражается через фундаментальные постоянные:

193

σ = 2π 5 k 4

15c 2 h3

Из рис. следует, что для каждой температуры кривые Планка имеют максимум что с ростом температуры максимум смещается в сторону более коротких длин волн, то есть

больших частот. Немецкий физик Вин установил, что длина волны λm , соответствующая максимальному значению спектральной плотности энергетической светимости АЧТ обратно пропорциональна его термодинамической температуре Т:

где C1 = 2,9 ×10−3 м× К .

Это первый закон Вина, или закон смещения Вина.

Второй закон Вина позволяет определить само значение максимальной спектральной плотности энергетической светимости rλm АЧТ при данной температуре Т:

где C2 = 1,29 ×10−5 Втм−3К−5 .

Законы Вина также могут быть получены из формулы Планка. Для этого нужно выразить точку максимума распределения и найти зависимость максимальной излучательной способности от температуры.

Вычисляя производную получим

Уравнение 5(1 - e− x ) = x может быть решено приближенно

(итерациями). Возьмём x0=0 и подставим его в левую часть, тогда в правая часть даст следующее приближение x1=5, подставляя его в левую часть получим x2=5(1-е-5)= 4,97. Видим, что второе приближение мало отличается от первого, следовательно можно его принять в качестве приближённого решения. В результате для первого закона Вина получим:

hc = 4,97

λkT

194

Что даёт коэфициенты, совпадающие с приведённой выше эмпирической формулой (12).

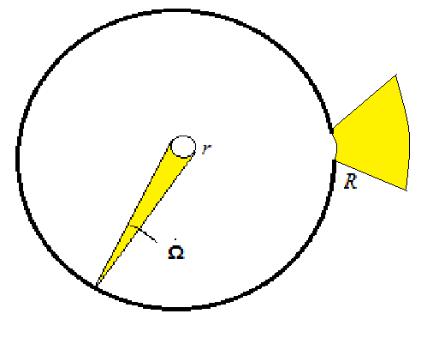
Приведем связь между интенсивностью I излучения абсолютно чёрного тела и равновесной плотностью энергии излучения u в окружающем пространстве. Для простоты вывода рассмотрим тело в виде сферической полости, радиусом R, а величину u вычислим в центре этой полости. По определению [ I ]=Дж/(c м2ср), то есть даёт мощность, выходящую из единичной площади тела в определённом направлении в расчёте на единичный телесный угол (в стерадианах ср).

Выделим в ценре полости небольшой шаровой объём, радиуса r. Этот объём виден из какой то точки полости под телесным углом U=πr2/R2. C с каждого квадратного сантиметра поверхности тела в 1 секунду на рассматриваемый объём падает энергия I U .

Поскольку энергия протекает через площадь πr2, вытекающая за секунду энергия равна должна иметь плотность u1: u1πr2c= I U или

Полная плотность энергии u складывается из излучения всей

поверхности полости, площадью 4πR2 в результате получим окончательную формулу:

Заметим, что если в сферической полости проделать небольшое отверстие, то энергетическая светимость этого отверстия RЭ будет определятся формулой (11), а через плотность энергии внутри полости выразится следующим образом:

Подробности вычислений можно найти в учебниках.

Основы квантовой механики**

Спектр водорода. Постулаты Бора

Простейшим атомом является атом водорода, состоящий из одного протона в ядре и одного электрона, движущегося в кулоновском электрическом поле ядра.

Водородоподобными ионами (изоэлектронными водороду) называют ионы Не+, Li++, Be+++ и

т.д., имеющие ядро с зарядом Ze и один электрон.

Среди оптических свойств атома важнейшим является его спектр излучения. Частоты линий ν в дискретном линейчатом спектре атома водорода описываются формулой Бальмера – Ридберга

где с – скорость света в вакууме; n и n1 – положительные целые числа, причем n1>n.

где Z – порядковый номер элемента в периодической системе Менделеева.

Спектр и энергетические уровни атома водорода были объяснены впервые с помощью постулатов Бора.

Первый постулат Бора (постулат стационарных состояний): в атоме существует набор стационарных состояний, находясь в которых атом не излучает электромагнитные волны. Стационарным состояниям соответствуют стационарные орбиты, по которым электроны движутся с ускорением, но излучение света при этом не происходит.

196

Правило квантования орбит: в стационарном состоянии атома электрон, движущийся по круговой орбите, имеет квантованные значения момента импульса, удовлетворяющие условию:

стационарного состояния в другое испускается или поглощается один фотон. Излучение фотона происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией. При обратном переходе происходит поглощение фотона. Энергия hν фотона равна модулю разности энергий в двух состояниях атома:

2. Корпускулярно-волновая двойственность свойств частиц вещества. Волны де Бройля

Физика атомов, молекул и их комплексов, в частности кристаллов, а также атомных ядер и элементарных частиц изучается в квантовой механике. Объекты микромира, изучаемые квантовой механикой, имеют линейные размеры порядка 10-6 ÷ 10-12 см. Если частицы движутся со скоростями υ << c , где с – скорость света в вакууме, то применяется нерелятивистская квантовая механика.

Основополагающей в квантовой механике служит идея о том, что корпускулярноволновая двойственность свойств, установленная для света, имеет универсальный характер. Все движущиеся частицы обладают волновыми свойствами.

Формула де Бройля устанавливает зависимость длины волны, связанной с движущейся частицей вещества, от импульса р частицы

H = h = 1,05 ×10−34 Дж × с. 2π

Длина волны де Бройля для частицы с массой m , имеющей кинетическую энергию

Wk ,

197

2mWk

Формула де Бройля экспериментально подтверждается опытами по рассеянию электронов и других частиц на кристаллах и по прохождению частиц сквозь вещество. Признаком волнового процесса во всех таких опытах служит дифракционная картина распределения электронов (или других частиц) в приемниках частиц.

Волновые свойства не проявляются у макроскопических тел. Длины волн де Бройля для таких тел настолько малы, что обнаружение волновых свойств оказывается невозможным.

Соотношения неопределенностей Гейзенберга

Волновые свойства микрочастиц вносят ограничения в возможность применять к таким частицам понятия координаты и импульса в их классическом смысле.

В классической физике также существуют ограничения в применении некоторых понятий к определенным объектам. Так, понятие температуры не имеет смысла применять для одной молекулы, понятие о точной локализации (пребывание в одной точке) неприменимо к определению положения в пространстве волны и т.д. Однако в классической механике определенному значению координаты частицы соответствуют точные значения ее скорости и импульса. В квантовой механике существуют ограничения в возможности одновременного точного определения координаты частицы и величины ее импульса. Эти ограничения связаны с корпускулярно-волновой двойственностью свойств микрочастиц.

локализована частица, описываемая волной де Бройля, если проекции ее импульса по осям

198

положение частицы на оси ОХ определено точно и x = 0 , то px = ∞ и значение

проекции импульса px становится совершенно неопределенным.

Соотношения неопределенностей накладывают в квантовой механике определенные ограничения на возможности описания движения частицы по некоторой траектории.

В классической теории в каждой точке траектории частица имеет определенные координаты x, y,z и определенный импульс p с проекциями по осям px , p y , pz . В

квантовой механике это реализуется только в тех случаях, когда частица движется в макроскопической области пространства (например, оставляет след на фотопластинке или экране осциллографа). Если, например, положение электрона зафиксировано с точностью, определяемой линейными размерами зерна фотоэмульсии, испытывающего воздействие

движется по определенной траектории с точно заданной в каждой точке скоростью.

Если частица движется в макроскопической области пространства, то соотношения неопределенностей существенно сказываются на характере движения частицы. Например, положение электрона, движущегося в атоме, может быть определено с точностью до

размеров атома, то есть Dx ~ 10−10 м . Неопределенность скорости υx оказывается при этом такого же порядка, что и сама скорость: Dυx » 106 м / с » υ. Траектория электрона в атоме с точно заданной в каждой точке скоростью не имеет смысла. Это вовсе не означает, что соотношения неопределенностей свидетельствуют о принципиальной ограниченности наших знаний о микромире. Эти соотношения лишь отражают ограниченную применимость понятий классической физики в области микромира.

Соотношения неопределенностей не вносят ограничений в возможность использовать в классическом смысле понятия координаты и импульса для макроскопических тел. Волновые свойства у таких тел не проявляются и поэтому для макроскопических тел соотношения

где DW – неопределенность энергии частицы, которая находится в течение времени Dt в

состоянии с энергией W . Энергия частицы в данном состоянии может быть определена тем точнее, чем дольше частица находится в этом состоянии.

199

Уравнение Шредингера**

Положение частицы в пространстве в данный момент времени определяется в

данной точке пространства: Ψ 2 = dω = ρ . Интенсивность волны де Бройля определяется

dV

величиной Ψ 2 .

Волновая функция Ψ(x, y,z,t ) является основной характеристикой состояния

микрообъектов (атомов, молекул, элементарных частиц). С ее помощью вычисляется среднее

значение физической величины L , характеризующей объект, находящийся в состоянии,

описываемом волновой функцией Ψ ,

Какому уравнению должна подчинятся волновая функция для состояния, когда энергия системы фиксирована (стационарное уравнение шредингера).

Волновое уравнение может быть записано в виде:

Для гармонической волны зависимость от времени определяется формулой

S (t, x) = A ×sin(ωt M kx) тогда заменяя вторую производную по времени соотношением