8504

отвергающий проверяемую гипотезу по полученной в наблюдении за случайной величиной Х выборке хВ = {1, 2, . . . } объёма . Критерий проверки гипотезы состоит из двух составляющих:

Во-первых, в качестве критерия принимается некоторая случайная величина с известным распределением при условии справедливости основной ( /0) и хотя бы частично известным для альтернативных гипотез ( / ) , = 1, … , . Кроме того, значения критерия должны быть вычисляемы по наблюдаемой выборке хВ, т.е. = ( ).

Во-вторых, строится Алгоритм (решающее правило) для критерия проверки, согласно которому гипотеза будет приниматься или отвергаться. Для этого, назовем критической областью критерия те значения величины , при которых гипотеза отвергается. Критическую область будем обозначать К . Тогда решающее правило критерия проверки будет следующим:

верки К отделяется от области принятия гипотезы, называются критическими точками критерия . Как построить критическую область критерия?

Принцип максимального правдоподобия утверждает, что наблюдаемые события имеют большую вероятность и наоборот, маловероятные события ненаблюдаемые. Согласно этому принципу, наблюдаемое значение критерия должно иметь в рамках проверяемой гипотезы большую вероятность. В противном случае, если вероятность наблюдаемой величины мала, проверяемую гипотезу нужно отвергать в пользу иных альтернативных гипотез.

Зададимся вероятностью ошибки 1-го рода, как наиболее значимой. Исключить такую ошибку при проверке гипотезы невозможно ( ≠ 0), на практике обычно эту вероятность задают достаточно малой величиной = 0,05; = 0,025; = 0,005 и называют уровнем значимости гипотезы.

Если из условия

82

можно определить критические точки однозначно, то задача построения критической области критерия решена. В противном случае, когда ещё остаётся свобода выбора критических точек, рассмотрим влияние альтернативных гипотез. Поскольку величина - есть вероятность принять неверную гипотезу 0 при условии справедливости альтернативной гипотезы , то

∫ ( / ) = 1 −

есть вероятность правильного отбрасывания 0 при условии справедливости и её называют мощностью критерия по отношению к альтернативной гипотезе . Поэтому при заданном уровне значимости , критическую область критерия нужно строить так, чтобы мощность критерия была максимальной (1 − ) по отношению ко всем альтернативным гипотезам.

Таким образом, критическими точками критерия являются квантили его распределения, определенные согласно уровню значимости проверяемой гипотезы.

Рис. 3.1. Двухсторонняя критическая область критерия К = { > 2, < 1} при наличии двух альтернативных гипотез 1, Н2

На рис. 3.1 приведена графическая интерпретация алгоритма построения критической области одномерного критерия. Видим, что структура критической области зависит от наличия альтернативных гипотез и их «расположения» относительно основной.

Рассмотрим примеры.

Критерий Смирнова-Граббса. Рассмотрим проблему отсева грубых ошибок при измерении нормальной случайной величины. Пусть мы

83

емой гипотезой является гипотеза о не грубой ошибке при измерении

данного измерения. Обычно на грубость измерения проверяются крайние точки наблюдений (максимальная и минимальная). Проверим на грубость измеренную максимальную температуру в рассмотренной выше выборке майских температурных измерений.

Видим, что при значимости проверяемой гипотезы в 10% критерий от-

разом, это измерение грубое и его лучше убрать из выборки. Вывод критерия зависит от точности измерения и значимости гипотезы, то есть риска ошибиться при отклонении верной гипотезы. Так, если уровень

является грубым.

Критерий Стьюдента о значимости измеренной величины. В стати-

стическом анализе очень часто используются критерии о значимости оценок различных величин, построенных по выборке. Проверяемой гипотезой является гипотеза о том, что истинная теоретическая величина u равна нулю H0 ={u = 0} , а в наблюдениях ее выборочный аналог uB отличен от нуля. Действительно ли наблюдаемое значение не нулевое (значимое), или это произошло случайно на рассматриваемой выборке? Для ответа на этот вопрос в дальнейшем мы будем использовать критерий Стьюдента рис. 3.2 :

84

Рис. 3.2. Критерий Стьюдента проверки значимости величины

ство степеней свободы выборки, потерянных при построении оценки. Для удобства часто вводится понятие жесткости критерия

( ) = .

Значимость проверяемой оценки имеет место быть при жёсткости > 1, когда проверяемая гипотеза о нулевом значении теоретической величины отвергается.

Например, в качестве проверяемой величины можно взять откло-

нение выборочной оценки от генеральной = − ̄. Проверяемая ги-

потеза и критерий

Понятно, что область принятия этой гипотеза со значимостью α совпадает с доверительным интервалом для оценки мат. ожидания при надежности = 1 − .

3.3.2. Критерий согласия Пирсона

Критериями согласия называются критерии проверки статистических гипотез о виде распределения случайной величины. Проверяемая гипотеза имеет вид:

0 = { ~ Х( , 1, 2, . . . ),

где 1, 2, . . . - принятые в гипотезе параметры распределения. Пирсон предложил и обосновал следующий критерий проверки гипотезы 0 по

85

отношению к единственной альтернативной противоположной гипотезе

строим, так же теоретические частоты для интервалов при усло-

вии справедливости проверяемой гипотезы 0. Теоретические частоты

где ( ) - функция распределения для случайной величины , – шаг интервалов гистограммы, +0.5 = 0,5( + +1) центры интервалов ги-

при достаточно большом объеме выборки имеет «хи-квадрат» распределение с − − 1 степенями свободы и может быть использована в качестве критерия для проверки гипотезы 0. Задаваясь уровнем значимостиможем однозначно определить правостороннюю критическую область критерия из уравнения

(2 > 2 ) = .

Его решение представляет собой правостороннюю квантиль «хи-квад-

рат» распределения 2 = 2 ( , − − 1) .

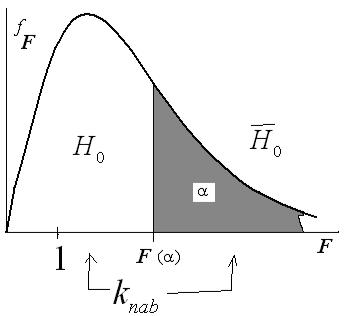
Рис. 3.3. Критическая область критерия Пирсона.

86

(отклонения частот значительны).

Числовой пример: Проверим гипотезу о нормальном распределении полуденных температур месяца мая для выборки, приведенной в лекции

мального распределения. Таким образам проверяемая гипотеза такова:

валов разбиения данных в гистограмме. Все результаты приведем в таблице и на рис.3.4.

87

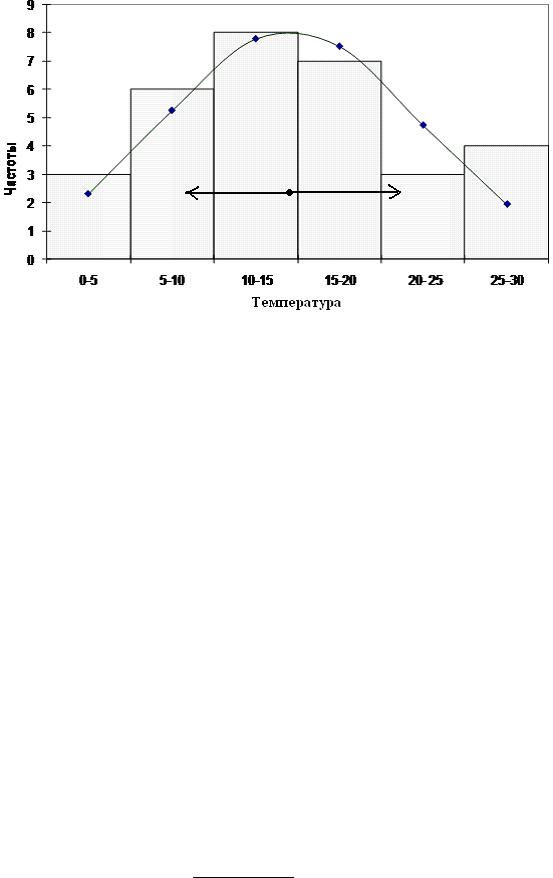
Рис. 3.4. Гистограмма наблюдаемых частот и кривая теоретических частот.

По заданному уровню значимости проверяемой гипотезы 0 определим критическую точку распределения «хи-квадрат» как правосторон-

(нет оснований ее отвергнуть), т.к. отклонения частот незначительны.

3.3.3. Критерий однородности выборок

Часто приходится сравнивать две или несколько нормальных выборок на их идентичность (наблюдаемость в них одой и той же нормальной величины). Пусть имеются две выборки наблюдений за случайными величинами

мых выборок проверим две гипотезы о равенстве параметров наблюдаемых случайных величин.

А). 0 = { 12 = 22} гипотеза о равенстве дисперсий. Воспользуемся критерием

( 2, 2)

1 2

= ( 12, 22) = 1−1, 2−1

имеющим - распределение Фишера. Вычисляем ≥ 1 и критическое значение как правостороннюю квантиль распределения по

88

заданному уровню значимости . При соотношении ≥ гипотеза отвергается иначе принимается.

Рис.3.5 Односторонний критерий Фишера.

В). После проверки равенства дисперсий можно проверить гипотезу

Проверяем критерии Стьюдента обычным образом в соответствии с заданным уровнем значимости гипотезы .

После проверки обоих критерий на равенство генеральных, можем говорить о том, что наблюдаемые выборки идентичны, т.е. наблюдаемые нормальные величины совпадают.

Пример. Рассматривая температуры мая, разобьем наблюдения первой половины месяца и второй на две выборки и сравним их на однородность.

89