8504

только при = 0. Если столбцы ( × )-матрицы представляют собой базис, то для любого -мерного вектора найдется -мерный вектор , для которого = . Компоненты вектора дают коэффициенты разложения вектора по этому базису.

Система линейных уравнений относительно переменных 1, … ,

11 1 + + 1 = 121 1 + + 2 = 2

1 1 + + =

может быть кратко записана в матричной форме в виде

= ,

где – матрица коэффициентов системы, а — вектор правой части.

1.2. Кластеризация

В этом разделе рассмотрим задачу кластеризации набора векторов (или точек) в группы или кластеры по близости этих векторов друг к другу и изложим классический метод кластеризации, называемый алгоритмом « -средних». Пусть имеется -мерных векторов 1, … , , которые требуется разбить по близости на кластеров. Обычно много меньше, чем . Конечно, когда векторы двумерные и можно видеть соответствующее им множество точек на плоскости, то разбить их на группы по близости не представляет особого труда. Другое дело, когда размерность векторов больше трех и не существует адекватного полного визуального их образа. В этом случае автоматическая кластеризация представляется единственным методом для решения этой трудной задачи.

Кластеризация широко применяется в различных областях, когда векторы представляют различные характеристики объектов: распределение больных по данным их медицинских анализов; классификация текстов по частотам, с которыми встречаются в этих текстах слова из выбранного словаря; распределение студентов по оценкам, полученных ими по выбранным предметам за определенный период обучения; разбиение людей на групп по результатам анкетирования, в котором на каждый вопрос возможен один из ответов, например, типа «сильно не

21

согласен», «не согласен», «нейтрален», «согласен», «сильно согласен», закодированных как −2, −1, 0, 1, 2; разбиение районов по среднемесячным количествам выпадающих осадков и температурам; распределение потребителей электроэнергии, представляемых 24-мерными векторами средних ежечасных расходов энергии за определенный период (скажем, за месяц), на группы похожих потребителей; распределение компаний, представляемых векторами, компоненты которых отражают их экономическое состояние, на группы с похожими показателями.

Обозначим кластеры 1, … , и принадлежность векторов кластерам будем задавать вектором R , компонента которого равна номеру группы, к которой принадлежит . Например, для = 5 и = 3 вектор = (3, 1, 1, 1, 2) означает, что 1 принадлежит группе 3, 2, 3 и 4 – группе 1, а 5 — группе 2. Кроме того, будем описывать группы множеством индексов элементов, принадлежащих группе . Для приведенного примера имеем 1 = {2, 3, 4}, 2 = {5}, 3 = {1}. Формально, это можно записать так: = { = }, т.е. — это множество всех индексов , для которых = . Введем понятие представителей кластеров (групп) — -мерных векторов 1, … , . Вообще говоря, ими могут быть любые векторы, даже не совпадающие с данными. Желательно, чтобы эти представители были бы ближе к векторам соответствующей группы,

т. е чтобы величины ‖ − ‖ были бы малы. Определим цель кластеризации как минимизация показателя

= ‖ 1 − 1‖2 + + ‖ − ‖2 / ,

означающего среднее значение суммы квадратов расстояний всех векторов до представителей их группы.

22

2. Элементы теории управления

2.1. Построение математической модели

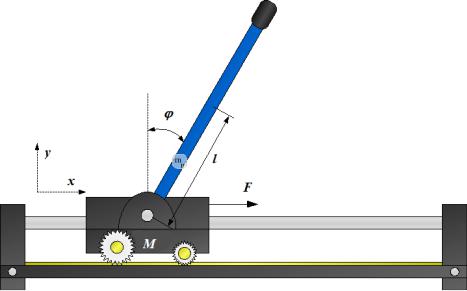
Рассмотрим механическую систему, представляющую собой однозвенный перевернутый маятник, шарнирно закреплённый на тележке (см. рис. 2.1). Тележка приводится в движение электродвигателем постоянного тока, напряжение на обмотке которого выберем в качестве управляющего воздействия.

Рис. 2.1. Схематическое изображение

Запишем уравнения движения системы, воспользовавшись подходом на основе уравнений Лагранжа. Для этого найдем выражения суммарной кинетической и потенциальной энергий. Кинетическая энергия системы представляет собой сумму кинетической энергии прямолинейного движения тележки тел, кинетической энергии поступательного движения центра масс маятника пост и кинетической энергии вращательного движения центра масс маятника вращ. Чтобы записать выражения указанных величин выберем в качестве переменных состояния положение тележки , отсчитываемое от произвольной точки, вы-

23

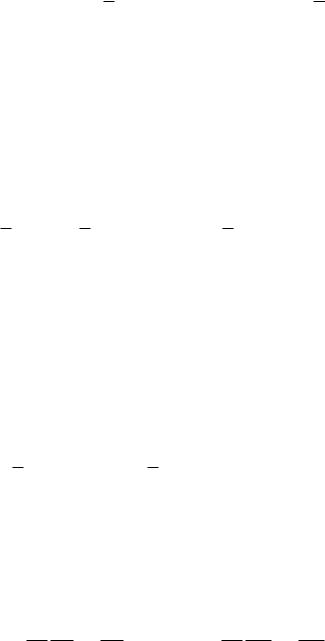
и кинетическая энергия вращательного движения центра масс маятника имеют вид

здесь — масса тележки, — момент инерции маятника. Теперь выразим координаты центра масс маятника и через переменные состояния:

где — расстояние от центра масс маятника до точки крепления, и запишем кинетическую энергию поступательного движения маятника:

где — масса маятника.

Для получения выражения потенциальной энергии выберем в качестве нулевого потенциального уровня горизонталь = 0, тогда:

= = cos .

Объединяя выражения для кинетической и потенциальной энергий, запишем функцию Лагранжа (лагранжиан) системы:

− ̇̇cos − cos . (2.1)

Теперь используя уравнения Лагранжа (уравнения движения в обобщенных координатах), запишем уравнения, описывающие динамику рассматриваемой системы:

где обобщенная сила порождена силой вязкого трения между колесами тележки и поверхностью, а сила — силой вязкого трения в оси электродвигателя. Приведем выражения указанных сил:

здесь — напряжение на обмотке электродвигателя, — коэффициент вязкого трения между колесом каретки и направляющей, — коэффициент момента вязкого трения в точке крепления маятника, а и —

24

конструктивные параметры. Подставим лагранжиан (2.1) и выражения (2.3) в уравнения (2.2), а затем упростим, после чего получим итоговые уравнения динамики:

Числовые значения параметров, входящих в уравнения (2.4), приведены в таблице 2.1.

Таблица 2.1. Параметры математической модели перевернутого маятника

Из физических соображений очевидно, что в отсутствии управления у маятника есть всего два положения равновесия: неустойчивое,

содержит неустойчивые состояния равновесия.

Рассмотрим произвольное состояние равновесия , принадлежащее

25

множеству E , и линеаризуем систему (2.4) в его окрестности:

Заметим, что уравнения (2.5) можно получить из (2.4) если воспользоваться приближениями cos ≈ 1 и sin ≈ , после чего отбросить все нелинейные слагаемые. Так как система (2.5) не приведена к нормальному виду, то характеристическое уравнение запишется как

Можно показать, что старший коэффициент уравнения положительный, коэффициент перед мономом первого порядка отрицательный, а свободный коэффициент равен нулю:

следовательно, не выполняется необходимое условие устойчивости, поэтому состояние равновесия является неустойчивым. Приведем также корни характеристического уравнения, которые были найдены для числовых значений параметров из таблицы 2.1 с использованием математического пакета:

Доказательство устойчивости состояний равновесия, принадлежащих множеству E , проводится аналогично.

Доказать, что система (2.4) в отсутствии управления не имеет состояний равновесия, отличных от тех, что принадлежат множе-

ствам E и E . Указание: положить в системе (2.4) скорости, ускорения и управление равными нулю, после чего найти решение полученной системы относительно и .

Доказать, что состояния равновесия, принадлежащие множеству E , устойчивы.

26

2.2. Синтез непрерывной системы управления 2.2.1. Синтез модального управления по состоянию

Рассмотрим задачу стабилизации перевернутого маятника, которая заключается в определении управления — закона изменения напряжения , подаваемого на обмотку мотора тележки, — при котором верхнее неустойчивое положение маятника станет асимптотически устойчивым. Подобное управление естественно назвать стабилизирующим.

Будем искать управление в классе линейных обратных связей по состоянию вида

управления позволяет добиться лишь локальной устойчивости. Последнее означает, что множество начальных состояний, для которых решение системы (2.4), замкнутой регулятором (2.6), стремится к состоянию

представляет собой некоторую окрестность этого состояния.

Система (2.7) является полностью управляемой, поскольку матрица управляемости C , имеет полный ранг:

Таким образом, рассматриваемая задача стабилизации имеет решение, то есть за счёт выбора коэффициентов обратной связи 1, … , 4 можно передвинуть собственное число 4 в левую полуплоскость комплексной плоскости, например, в точку ′4 = − 4, и тем самым добиться устойчивости верхнего положения маятника.

27

Для синтеза искомого регулятора построим преобразование, приводящее матрицу к блочному нижнетреугольному виду так, чтобы собственное число 4 располагалось в начале главной диагонали. Для этого левый собственный вектор 4, соответствующий 4, дополним произвольными векторами до линейно независимой системы. В качестве такого дополнения можно выбрать, например, векторы стандартного базиса:

Поскольку матрица блочная нижнетреугольная, то, чтобы передвинуть полюс 4 в точку ′4, нужно выбрать 1 как решение уравнения 6.376+ 0.305 1 = −6.376. Таким образом, находим матрицу регулятора Θ =

− 41.810, 0, 0, 0 . Возвращаясь к прежним переменным, получаем

Θ = Θ −1 = 0, −38.531, 15.225, −5.626 ,

следовательно, закон управления имеет вид

28

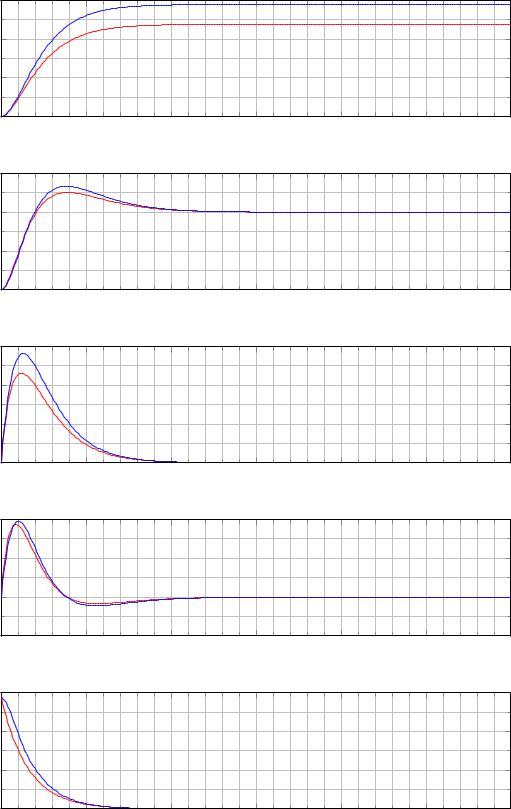
На рисунке 2.2 показаны результаты моделирования движения маятника и тележки при использовании регулятора (2.9) как для линеаризованной системы (2.5), так и для исходной нелинейной системы (2.4). В первом случае соответствующие кривые изображены красным цветом, а во втором — синим. Из представленных графиков видно, что при стабилизации маятника происходит постепенное смещение тележки в сторону от начального положения. На практике это может привести к тому, что смещение превысит максимально разрешённое, в результате чего процесс стабилизации прервётся и маятник опрокинется. Нетрудно видеть, что причина такого поведения системы заключается в отсутствии у нее асимптотической устойчивости, так как при построении регулято-

соответствующие числам 3 и 4, до линейно независимой системы. Например, возьмём векторы стандартного базиса 1 и 2, тогда матрица преобразования принимает вид

Применяя указанное преобразование к системе (2.7), получаем:

29