
8504
.pdf-выборка должна быть представительной, т.е. сохранять в себе пропорции генеральной совокупности,
-объём выборки должен быть небольшим, но достаточным для того, чтобы полученные результаты её анализа обладали необходимой степенью надёжности,
-данные в выборке не должны бать «засорены» грубыми измерениями, содержащими нетипично большие ошибки измерений.
Отметим, что в более строгом смысле выборку можно представить
как случайную многомерную величину Х = {Х1, Х2, Х3, . . . . . . , Х } = |
||
{Х ; = 1, }, у которой все компоненты |
|
|
Х |
i распределены одинаково и по |
|
|
|
|
закону распределения наблюдаемой случайной величины. В этом смысле |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выборочные значения х B |
есть одна из реализаций величины Х В . |
|||||||||||||||||||||
Возможные значения элементов выборки |
х |
B |
|
|
i |
|
|
|
|
, называ- |
||||||||||||
ются вариантами |
|
|
|
|
|
|
|
|
|
|
= |
{x |
; i = 1, n} |
|
||||||||
x |
j |
выборки, причём число вариант m меньше, чем |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
объём выборки |
n |
. Варианта может повторяться в выборке несколько |
||||||||||||||||||||
раз, число повторения варианты |
x |
j в выборке называется частотой ва- |
||||||||||||||||||||
рианты |
n |
j . Причём, |
1 |
2 |
|
|
m |
|
. Величина |
w |
j |
= n |
j |
/ n |
называется |
|||||||
|
|
|
|
|
n + n |
|
+..... + n |
|
= n |
|
|
|
|
|
|
|
||||||
относительной частотой варианты x j .
Упорядоченный по возрастанию значений набор вариант совместно с соответствующими им частотами называется вариационно-ча- стотным рядом выборки:
|
|
V |
xn |
={x |
j |
, n |
; j =1, m} |
; |
V |
xw |
={x |
j |
, |
j |
; j =1, m} |
. |
||
|
|
|
|
|
|
j |
|
|
|
|
|
|||||||
Ломаная линия, соединяющая точки вариационно-частотного ряда |
||||||||||||||||||
на плоскости |
(x, n) |
или |
(x, ) |
называется полигоном частот. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вариационно-частотный ряд имеет существенный недостаток, а именно, не наглядность полигона в случае малой повторяемости вариант, например, при наблюдении непрерывного признака его повторяемость в выборке маловероятна. Более общей формой описания элементов выборки является гистограмма выборки.
Для построения гистограммы разобьём интервал значений вы-
борки |
R = x |
m ax |
− x |
m in на m интервалов |
h |
j |
= (x |
j |
, x |
j +1 |
) |
длины h = R / m с гра- |
||||
ницами x j |
= xmin + h ( j −1) . |
Число элементов выборки |
х |
B , попадающих в |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
интервал, |
h j называется частотой n j интервала, кроме того вводятся сле- |
|||||||||||||||
дующие величины: |
|
|
|
|
|
|
|
|
|
|
|
|||||
71

|
j |
|
|
||
w |
j |
|
|
|
|
= n |
j |
|
/ n |
|
|
|
|
= |
|
j |
/ h |
|
|
|
~ относительная частота интервала,
j ~ плотность относительной частоты интервала.
Совокупность интервалов, наблюдаемой в выборке случайной величины и соответствующих им частот, называется гистограммой выборки. Различаются гистограммы частот, относительных частот и плотности частоты и обозначаются соответственно:
H xn ={hj , n j ; j =1, m}, H x ={hj , j ; j =1, m}, Hxw ={hj , wj ; j =1, m}.
Для частот гистограммы выполнены следующие условия нормировки:
m n j
j =1
=
n
,
m j
j =1
=
1
,
m w j h =1
j =1
Число интервалов гистограммы m должно быть оптимальным, чтобы, с одной стороны, была достаточной повторяемость интервалов, а с другой стороны не должны сглаживаться особенности выборочной ста-
тистики. Рекомендуется значение |
m 1+ 3,2 lg(n) . На плоскости |
(x, n) |
ги- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
стограмма представляется ступенчатой фигурой. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
Помимо полигона и гистограммы выборка характеризуется следу- |
|||||||||||||||||||||||||||||||||||
ющими основными числовыми характеристиками: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
= |
|
x |
|
|
|
~ выборочное среднее; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
В |
n |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
= |
|
|
|
|
|
− x |
|
|
) |
2 |
~ выборочная дисперсия; |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
В |
|
|
|
|
|
i |
B |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
D |
|
n |
|
|
|
(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
В |
= |
|
|
|
D |
|
|
|
|
~ выборочное среднеквадратическое отклонение; |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S |
|
2 |
= |
|
|
|
|
|
|
(x |
|
− x |
|
) |
2 |
~ исправленная выборочная дисперсия; |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
i |
B |
|
|
|
||||||||||||||||||||||||||||
|
|
n −1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
i |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
S = |
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
~ исправленное выборочное среднеквадратическое |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
отклонение (выборочный стандарт). |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
Пусть, например, дана выборка полуденных температур месяца |
|||||||||||||||||||||||||||||||||||
Май своим вариационно-частотным рядом с объёмом |
n = 31 |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
хj |
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
7 |
8 |
12 |
|
14 |
16 |
19 |
|
23 |
25 |
|
27 |
|
30 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
nj |
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
2 |
3 |
4 |
|
2 |
3 |
6 |
|
2 |
1 |
|
|
3 |
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72
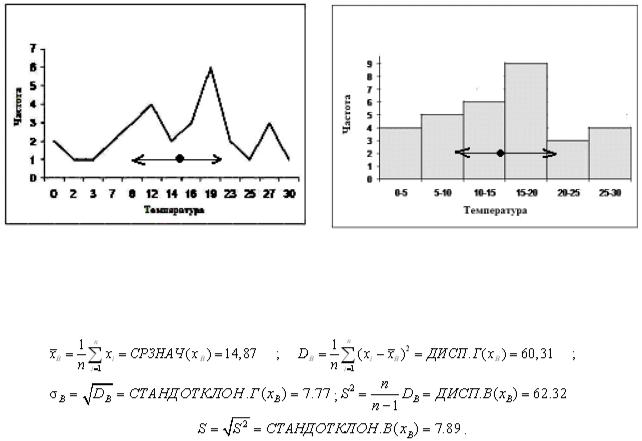
Полигон с количеством вариант
тервалов |
m = 6, |
h = 30 / 6 = 5 |
, для |
|
|
m =13 |
и гистограмма с количеством ин- |
|
этой выборки приводятся на рис.1.10.
Рис. 1.10. Полигон и гистограмма частот выборки
Расчёт основных выборочных характеристик может быть легко проведен с помощью статистических функций приложения Excel:
Выборочное среднее xB и выборочный стандарт S , характеризующие центр и размах выборочных значений, так же представлены на рис. 1.10.
Напомним, что все числовые характеристики выборки являются случайными величинами, поскольку получены по случайно взятой выборке. На элементах другой выборки наблюдений над той же случайной величиной Х числовые характеристики в общем случае изменят свое значение. Генеральные характеристики, полученные по генеральной выборке, являются величинами постоянными. Сразу встает вопрос о соотношении генеральных и выборочных характеристик для наблюдаемой случайной величины.
Выборочные распределения. Рассмотрим нормальную выборку
XB = Xi , то есть выборку наблюдений за нормальной случайной величиной X = N (m, σ) . Тогда случайная величина среднего выборочного
73

Х |
В |
|
=
1 |
n |
|
Х i |
||
n |
||
i=1 |
||
|
так же является нормальной
X |
B |
|
= N(m,σ / 
n)
. Здесь
X |
i |
= N (m, σ) |
|
|
нормальные случайные величины, совпадающие с наблюдаемой величиной. Рассмотрим стандартные нормальные величины ξ = N (0;1) :
0 = X B − m , i = X i − m
/  n
n
ипостроим из них случайные величины Пирсона 2n и Стьюдента t n :
|
2 |
|
|
= |
|
|
|
|
|
|
n−1 |
|
||
|
|
t |
n−1 |
|
|
|
|
||
n |
|
|
|
1 |
n |
|
|
|
|
|
|
|
|
nD |
|
|
n −1 |
|||
i |
= |
|
(Xi |
− m) |
2 |
= |
= |
|||||||||||||
|
|
2 |
|
2 |
|
2 |
||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
i=1 |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
|
0 |
|
|
= |
|
X |
B |
− m |
= |
X |
B |
− m |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
n −1 |
|
|
n |
||||||
2 |
/(n −1) |
|
|
/ |
|
|
S / |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
S |
2 |
|
.
,
Отсюда видно, что случайная величина выборочной дисперсии распределена пропорционально «Хи-квадрат» случайной величине с − 1 степенью свободы, а отклонение выборочного среднего от математического ожидания распределено пропорционально -величине Стьюдента с − 1 степенью свободы. При сравнении двух выборок объёмов 1 и 2 часто используется случайная величина Фишера [8] со степенями свободы 1 и
2:
|
|
2 |
/ |
|
|
= |
1 |
1 |
. |
2 |
|
|||
1, 2 |
|
/ |
||
|
|
2 |
2 |
|
Распределения этих величин, как функций от стандартных нормальных величин, хорошо изучены и построены их функции распределения, обратного распределения и плотности вероятности распределения. Ниже на рис. 1.11-1.13 представлены графики и функции Excel для их вычисления.
Рис. 1.11. Функции распределения величины Пирсона
74

Рис.1.12. Функции распределения величины Стьюдента
Рис. 1.13. Функции распределения величины Фишера
3.2.1. Статистические оценки
Пусть распределение наблюдаемой случайной непрерывной величины (признак генеральной совокупности) задаётся функцией плотности вероятности ( , ), где параметр или параметры распределения. Допустим, что вид функции ( , ) известен или ограничен некоторым классом функций, а параметр неизвестен и должен быть оценён по вы-
борке хВ = { , } = {1, 2, . . . }, где – объём выборки.
Точечной статистической оценкой параметров распределения или характеристик наблюдаемой случайной величины X называется построенная по данным выборки объема n величина:
|
= |
( |
, |
, . . . ). |
|
|
1 |
2 |
|
75

Например, статистическими оценками математического ожидания вели-
чины могут быть такие оценки: = ̄, = 0.5( |
+ |
) или = |
|||
|
|
|
|
|
|
( |
+ |
)/6. |
|
|
|
|
|
|
|
|
|
|
|
Оценка |
* |
n является случайной величиной, т.к. зависит от случай- |
ной выборки. Для того, чтобы оценки, получаемые по данным различных
выборок, соответствовали истинному значению параметра |
|
, оценка |
|
||
должна удовлетворять следующим требованиям [8]. |
|
|
Оценка должна быть несмещенной, т.е. её математическое ожидание должно совпадать с истинным значением параметра для любого объёма n
М ( * ) = n
или хотя бы асимптотически несмещённой:
* |
) |
М ( |
|
n |
|
→ n→
.
Оценка должна быть состоятельной, т.е. с ростом объёма выборки оценка должна сходиться по вероятности к истинному значению параметра:
P( * n
− 
) →1 n→
для любого
0 .
Для состоятельности оценки достаточно выполнения следующего:
D( * ) →0 .
n n→
Построенная оценка для использования на практике должна быть эффективной, т.е. её дисперсия должна быть минимальной среди всех возможных оценок при фиксированном объёме выборки:
* |
) |
|
D( |
n ef |
|
|
|
|
=
min
* |
) |
D( |
|
n |
|
.
Коэффициент эффективности оценки
k |
|
* |
* |
) |
|
ef |
= D( |
nef |
) / D( |
||
|
|
n |
|
||
показывает
степень эффективности оценки |
* |
k |
ef |
( * ) →1 |
, то говорят об |
|
n , если |
|
n |
n→ |
|||
асимптотической эффективности оценки. Часто говорят о порядке интенсивности оценки если выполняется для ее дисперсии условие:
* |
) = |
|
1 |
|
D( |
|
|
p |
|
n |
|
|
||
|
|
n |
|
|
.
Отметим, что на практике не всегда удаётся удовлетворить всем перечисленным требованиям к оценке, но введённые свойства оценок позволяют проранжировать имеющиеся оценки по их качеству.
Как пример рассмотрим оценки математического ожидания M ( X ) = m и дисперсии D( X ) = d наблюдаемой случайной величины Х.
76

Построим точечные оценки:
m*
=
xB
,
d |
* |
= D |
|
|
|
|
|
 |
и рассмотрим их свойства.
Поскольку можно вычислить, что для оценки m* справедливо:
M (m* ) = m ; D(m* ) (d / n) → 0 при n → ,
то из этого следует несмещённость и состоятельность оценки m*. Рассматривая же оценку d * , можно получить что:
M (d |
* |
) = |
n −1 |
d d |
|
||||
|
n |
|||
|
|
|
|
;
* |
) |
D(d |
1 n
→0 n→
.
Из чего следует состоятельность, но смещённость оценки d*. Смещёность оценки здесь легко может быть исправлена, если рассмотрим оценку:
d |
* |
= |
n |
D |
= S |
2 |
. |
|
|||||||
|
|
|
|
|
|||
|
|
|
n −1 |
 |
|
|
|
|
|
|
|
|
|
|
Оценка |
d |
* |
= S |
2 |
является уже не только состоятельной, но и несмещён- |
||||||
|
|
||||||||||
|
|
|
|
||||||||
ной, так как M (d |
* |
) = d . Величина S |
2 |
поэтому называется исправленной |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
(несмещённой) выборочной дисперсией, а величина |
S |
- исправленным |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
среднеквадратическим выборочным отклонением (выборочный стандарт).
Существует ряд методов построения точечных оценок с определенными свойствами. Например:
Метод моментов, приравнивая нужное количество моментов случайной величины к выборочным моментам
B (θ) = b (x ) |
|
|
|
= |
(x , x |
,...x ) |
||
|
|
|
|
|
* |
* |
|
|
k |
k |
i |
|
|
n |
n |
1 2 |
n |
можно получить состоятельные, но необязательно несмещенные, оценки всех параметров. Напомним вычисление центральных моментов случайной величины и наблюдаемой выборки
B (θ) = (x − m)k f (x, )dx , b (x ) = |
1 |
n |
|
|
(x − x |
)k |
|||
|
X n i=1 i B
Вметоде максимального правдоподобия максимизирую функциюikk
правдоподобия
L(x1 , x2 ,... xn , ) =
f |
X |
(x |
, ) |
|
1 |
|
f X
(x2
, ) …
f |
X |
|
(x |
n |
, ) |
|
|
,
выражающую вероятность получения наблюдаемой выборки
L(xi , n ) = max L(xi , ) |
|
L(xi , ) = 0 , n* =n* (x1, x2 ,...xn ) |
|
|
|||
|
|
||
|
|
77

можно получить не только состоятельные, но и эффективные оценки.
Интервальные оценки в отличие от точечных оценок типа * за- n
дают интервал значений, где оцениваемый параметр находится с задан-
ной вероятностью. Дело в том, что точность оценки |
θ −θ |
n |
ε |
нами пока |
||||
|
|
|
|
* |
|
|
|
|
не рассматривалась, а в силу случайности оценки |
n можно говорить |
|||||||
|
|
|
* |
|
|
|
|
|
только о вероятности того, что оценка имеет некоторую точность |
ε |
. |
||||||
|
|
|
|
|
|
|
|
|
Надёжностью оценки (доверительной вероятностью) называется |
||||||||
вероятность |
γ |
, с которой оцениваемый параметр находится в интер- |
||||||
|
|
|
|
|
|
|
|
|
вале:
|
|
− |
|
|
|
+ |
|
* |
|
|
* |
|
|
||
|
n |
|
|
|
n |
|
|
.
Полуширина доверительного |
интервала |
|
|
|
|
|
называется |
точностью |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
оценки, соответствующей надёжности |
|
. Для построения доверитель- |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
ного интервала (нахождения по |
|
величины |
|
|
|
) необходимо знать закон |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
распределения оценки случайной величины |
|
* |
и решить доверительное |
||||||||||||||||||||||||
|
n |
||||||||||||||||||||||||||
уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
ε) = γ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
P( θ −θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Рассмотрим некоторые примеры. Пусть в выборке |
|
B |
i |
|
|||||||||||||||||||||||
наблюдается нормальная случайная величина |
|
|
|
х |
|
= {x |
; i = 1, n} |
||||||||||||||||||||
X |
= N (m, σ) |
|
c неизвест- |
||||||||||||||||||||||||
ными параметрами распределения m и |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А). Построим доверительный интервал для математического ожи- |
|||||||||||||||||||||||||||
дания m: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
−ε |
γ |
|
m x |
+ε |
γ , |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
B |
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m = X |
|
|
|
|
|
|
|||
принимая за точечную оценку m, величину |
|
|
* |
|
|
|
и учитывая, что ве- |
||||||||||||||||||||
|
|
|
|
|
B |
||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
личина (xB −m) /(S / n) = tn−1 |
имеет распределение Стьюдента с n −1 степе- |
||||||||||||||||||||||||||
нью свободы. |
|
|
|
|
|
|
|
|
|
|
|
относительно |
|
при заданном зна- |
|||||||||||||
Решение уравнения |
|
|
B |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
P( x −m ε) = |
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
чении эквивалентно решению уравнения: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x |
− m |
|
|
ε |
|
|
|
= γ , или Р( t |
t ) = . |
|
|
|
|
||||||||||||
P |
B |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S / |
n |
|
S / |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||||||||||||||||||
Его решение получим в виде |
|
= t S / |
|
n , где tγ = tobr (1− γ, n −1) двухсто- |
|||||||||||||||||||||||
ронняя квантиль Стьюдента (рис. 2.1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
78

Рис. 2.1. Двухсторонняя квантиль Стьюдента
|
|
|
В). Построим теперь доверительный интервал для среднеквадрати- |
||||||||||||||||||||||||||||||||
ческого отклонения |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
≤ ≤ + . |
|
|
|
|
|
|
|
||||||||||
Принимая |
|
за оценку |
|
величину |
|
* |
= S |
|
и |
учитывая, |
что величина |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
n−1 |
, имеет |
2 |
-распределение с n - 1 степенью свободы. Ре- |
||||||||||||||||||||||
S |
(n −1) / |
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
шение уравнения P( S − ) = относительно |
|
|
при заданном пара- |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
метре |
|
эквивалентно решению уравнения: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р(2 |
< |
2( −1) |
< 2) = , |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
2 |
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
тогда получим его решение в виде |
S |
2 |
n −1 |
|
2 |
S |
2 |
n −1 |
, |
где величины |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
obr |
|
1 |
|
|
|
являются правосторонними «хи-квадрат» квантилями |
||||||||||||||||||||||||||
|
= |
( |
|
|
, n −1) |
||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 2.2).
Рис. 2.6. Двухсторонняя «хи-квадрат» квантиль
79

Пример. Наблюдается выборка полуденных температур в Мае объё-
мом n =31 со средним выборочным значением |
x |
B |
=14,87 |
и несмещённой |
||||
дисперсией |
S |
2 |
= 62.32 |
. Построить доверительные интервалы для неиз- |
||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
вестного математического ожидания m и среднеквадратического отклонения при надёжности = 0,95 .
Исправленное выборочное среднеквадратическое отклонение
S = 7.89 .
Через обратное распределение Стьюдента находим
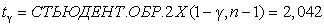 , тогда
, тогда
|
γ |
= 2.042 7,89 / |
31 = 2.894 |
|
|
|
и то-
гда доверительный интервал для математического ожидания m будет:
14.87+2.894 < m <14.87+2.894 или 11.976< m <17.674.
Для построения доверительного интервала среднеквадратического отклонения через обратное распределение «Хи-квадрат» находим
тогда:
,
6.305 = 7.89 |
31−1 |
σ 7.89 |
31−1 |
=10.546 . |
|
49.98 |
16.74 |
||||
|
|
|
3.3. Проверка статистических гипотез
Имея дело со случайными величинами, в различных областях человеческой деятельности часто приходится высказывать предположения о виде распределения случайной величины или о значениях её параметров. Эти предположения строятся с целью прогнозирования поведения случайной величины и принятия решений в условиях неопределённости.
Статистической гипотезой называется любое предположение о виде распределения случайной величины ( , ) или/и о значении неизвестных параметров распределения :
H ={X ~ f X (x, ); = 0 } – статистическая гипотеза. Высказанная статистическая гипотеза должна быть проверена по
результатам наблюдений (измерений) случайной величины , в результате чего, гипотеза принимается или отвергается с определённой степенью риска совершить ошибку. Примером статистической гипотезы может быть предположение о том, что наблюдаемая в выборке случайная величина является нормальной с определёнными значениями параметров:
80
