
8504
.pdf
матрицу замкнутой системы: |
|
0.131 2 |
0 |
0 |
|
|
0.131 1 |
|
|||||
0.305 1 |
6.376 + 0.305 2 |
0 |
0 |
|
, |
|
= + Θ = |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
здесь для упрощения записи элементы матрицы, не влияющие на вычисление параметров обратной связи, обозначены символом . Таким образом, исходная задача свелась к отысканию параметров 1 и 2, при которых справедливо равенство
det |
− |
0.131 1 |
0.131 2 |
′ |
′ |
(2.11) |
|
0.305 1 |
6.376 + 0.305 2 |
= ( − 3)( − 4). |
|
||
Легко проверить, что условие (2.11) равносильно системе уравнений
6.376 + 0.131 1 + 0.305 2 = −13.0, |
0.833 1 = 38.25, |
разрешая которую, находим коэффициенты регулятора 1 = 45.918,2 = −83.250. Наконец, возвращаясь к исходным переменным, получаем следующий закон управления:
= 45.690 − 76.718 + 34.945 − 11.280 |
̇ . |
(2.12) |
̇ |
|
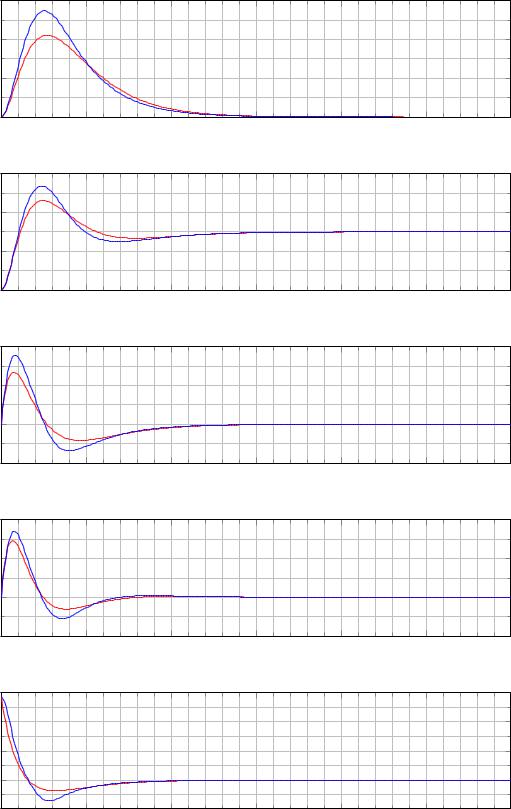
На рисунке 2.3 приведены графики управления и переходных процессов как в линейной (2.5), так и в нелинейной (2.4) системах, замкнутых построенным регулятором (2.12). В первом случае соответствующие кривые изображены красным цветом, а во втором — синим. Из представленных графиков видно, что регулятор (2.12), помимо устойчивости вертикального положения маятника, обеспечивает и устойчивость положения тележки, тем самым ограничивая её отклонение от начального положения. Однако максимальное значение управления, по сравнению с предыдущим случаем, выросло примерно в два раза. На практике это может привести к поломке установки, поскольку управление
— напряжение, подаваемое на обмотку электродвигателя, — не должно быть слишком большим. Чтобы ограничить управление, нужно уменьшить коэффициенты обратной связи, для этого желаемые собственные числа нужно выбирать ближе к мнимой оси. В то же время управление должно обеспечивать замкнутой системе заданные показатели качества, такие как время установления, коэффициент перерегулирова-
31
|
0.42 |
|
|
|
|
|
|
|
|
|
0.28 |
|
|
|
|
|
|
|
|
|
|
|
0.14 |
|
|
|
|
|
|
|
|
|
|
0.00 |
0.5 |
1.0 |
1.5 |
2.0 |
|
2.5 |
|||
|
0.6 |
|
|
|||||||
|
0.2 |
|
|
|
|
|
|
|
|
|
−0.2 |
|
|
|
|
|
|
|
|
|
|
|
−0.6 |
0.5 |
1.0 |
1.5 |
2.0 |
|
2.5 |
|||
|
2.8 |
|
|
|||||||
̇ |
1.4 |
|
|
|
|
|
|
|
|
|
0.0 |
|
|
|
|
|
|
|
|
|
|
|
−1.4 |
0.5 |
1.0 |
1.5 |
2.0 |
|
2.5 |
|||
|
9.0 |
|
|
|||||||
̇ |
4.5 |
|
|
|
|
|
|
|
|
|
0.0 |
|
|
|
|
|
|
|
|
|
|
|
−4.5 |
0.5 |
1.0 |
1.5 |
2.0 |
|
2.5 |
|||
|
48 |
|
|
|||||||
|
32 |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
−16 |
|
|
|
|
|
|
|
, её скорости |
|
Рис. 2.3. Графики зависимости от времени положения тележки |
|
|||||||||
|
|
0.5 |
1.0 |
1.5 |
2.0 |
|
2.5 |
|
||
, угла отклонения маятника |
|
, угловой скорости маятника |
|
управления |
|
|||||
|
и |
|
|
|||||||
для линейной (красный цвет) и нелинейной (синий цвет) систем, замкнутых |
||||||||||
̇ |
|
|
|
|
|
|
̇ |
|
|
|
регулятором (2.12); начальные условия 0 = |
0.0, −0.6, 0.0, 0.0 . |
|
||||||||
|
|
|
|
|
32 |
|
|
|
|
|
ния и др. Хорошо известно, что для повышения быстродействия системы (уменьшения времени установления) желаемые собственные числа следует выбирать подальше от мнимой оси, однако коэффициенты обратной связи в этом случае получаются достаточно большими. Таким образом, быстродействие системы и максимальное значение управления в общем случае являются противоречивыми критериями при выборе желаемых собственных чисел в задаче модального управления.
2.2.2. Синтез линейно-квадратичного управления
В предыдущем разделе было отмечено, что при решении задачи стабилизации необходимо учитывать как быстродействие системы, так и величину управляющего воздействия. Это приводит к задаче оптимизации, в которой критерий оптимальности отражает оба указанных показателя. Таким критерием естественно выбрать квадратичный функционал
( ) = |
∞ |
|
+ , |
(2.13) |
0
здесь первое слагаемое отвечает за быстродействие системы, а второе — за максимальное значение управления, весовые матрицы = 0
и= 0 задают приоритет каждой из компонент состояния и управления соответственно. Напомним, что запись 0 означает, что матрица неотрицательно определена, то есть все её собственные числа неотрицательны. Аналогично, запись 0 означает, что матрицаположительно определена и все её собственные числа положительны. Задача управления линейной системой вида (2.5) с квадратичным кри-
терием (2.13) называется задачей линейно-квадратичного управления.
Прежде чем переходить к синтезу линейно-квадратичного управления перевернутым маятником (2.5), напомним теорему существования
иединственности [Kwakernaak1977].
Теорема 2.1. Предположим, что пара матриц |
|
|
стабилизируе- |
||||||||||
ма, а пара |
|
детектируема, тогда: во-первых, |
существует единствен- |
||||||||||
|
|
( , ) |
|
||||||||||
ное неотрицательно |
определенное |
решение |
алгебраического |
||||||||||
|
( , ) |
|
|
|
|||||||||
уравнения Риккати |
|
|
|
−1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
= 0; |
|
(2.14) |
||||||
|
|
|
+ + − |
|
|
|
|
||||||
33
во-вторых, если есть решение уравнения (2.14), то управление |
|
= −−1 , |
(2.15) |
является стабилизирующим, то есть все собственные числа матрицы замкнутой системы = − −1 расположены в левой полуплоскости; в-третьих, управление (2.15) является оптимальным, то есть доставляет минимум функционалу (2.13), при этом
min ( ) = 0 0.
Таким образом, для синтеза линейно-квадратичного управления (2.15) требуется найти решение алгебраического уравнения Риккати (2.14). Аналитически это удается сделать лишь в достаточно вырожденных случаях, поэтому чаще всего для вычисления решения используют численные методы и математические пакеты. Например, в пакете MATLAB для решения алгебраического уравнения Риккати используется функция care, которая имеет следующий синтаксис:
[X,L,G] = care(A,B,Q,R),
здесь матрица есть неотрицательно определенное решение уравнения Риккати (2.14), вектор содержит собственные числа матрицы −(матрицы замкнутой системы) и, наконец, = −1 есть матрица обратной связи.
Вернемся к задаче стабилизации перевернутого маятника с помощью линейно-квадратичного управления. Сначала рассмотрим случай= и = 1. С физической точки зрения такой выбор матриц означает, что мы одновременно «минимизируем» и управление, и компоненты вектора состояния.
В разделе 2.2.1 было показано, что система (2.7) является полностью управляемой. Положим = , тогда = = и легко проверить, что пара матриц , является наблюдаемой. Действительно,
rank O , |
= rank , , 2, 3 = 4. |
Таким образом, согласно теореме 2.1 существует решение рассматриваемой задачи линейно-квадратичного управления. Теперь, используя
34
математический пакет, найдем решение уравнение Риккати:
= |
|
8.094 |
−6.343 |
|
3.299 |
−0.927 |
, |
|
|
|||
−6.343 |
128.590 |
−50.344 |
18.222 |
|
|
|||||||
|
|
|
|
|
3.299 |
−50.344 |
|
20.174 |
−7.255 |
|
|
|
|
|
|
|
|
|
18.222 |
|
−7.255 |
|
|
|
|
следовательно, |
|
|
−0.927 |
|
2.652 |
|
|
|
||||
|
|
искомый закон управления имеет вид |
|
|
|
|||||||
= − |
−1 |
|
|
= − 39.897 + 15.704 − 5.910 |
̇ . |
(2.16) |
||||||
|
|
|
|
|||||||||
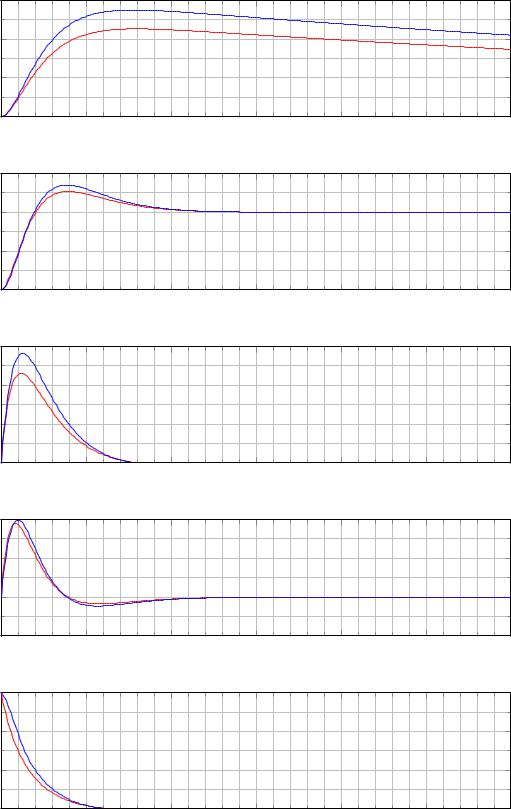
На рисунке 2.4 приведены графики |
управления и переходных про- |
|||||||||||
|
̇ |
|
|
|
||||||||
цессов в линейной системе (2.5), замкнутой регулятором (2.16), а также, для сравнения, графики переходных процессов в исходной нелинейной системе (2.4) при использовании этого же регулятора. Теорема 2.1 гарантирует асимптотическую устойчивость матрицы замкнутой системы, однако характеристики переходных процессов для различных компонент состояния могут быть разными. Например, время установления по компоненте примерно в 30 раз меньше, чем время установления по компоненте . Поскольку соответствует положению тележки, то на практике относительно долгое время установления по этой компоненте никак не сказывается на стабилизации маятника. Тем не менее попробуем построить управление, которое позволяет сократить время уста-
новления по компоненте .
Положим = diag 100, 1, 1, 1 и = 1, то есть в целевом функционале увеличим весовой коэффициент при компоненте в 100 раз по сравнению с предыдущим случаем. Нетрудно проверить, что можно положить = diag 10, 1, 1, 1 , тогда пара матриц , будет наблюдаемой, а, значит, существует единственное положительно определенное решение уравнения Риккати (2.14), которое может быть найдено с помощью математического пакета:
= |
118.100 |
−74.604 |
40.236 |
−10.945 |
, |
|
|
|||||
−74.604 |
177.575 |
−76.353 |
25.403 |
|
|
|||||||
|
|
|
|
|
40.236 |
−76.353 |
34.023 |
|
|
|
|
|
|
|
|
|
|
−11.069 |
|
|
|
||||
|
|
|
|
−10.945 |
25.403 |
−11.069 |
3.705 |
|
|
|
||
следовательно, |
закон управления имеет вид |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
−1 |
|
|
|
|
|
̇ |
|
|
(2.17) |
||
= − |
|
= 10 − 47.001 + 19.426 − 6.951 |
̇ . |
|||||||||
|
|
|
|
|||||||||
Графики переходных процессов и управления как в линейной систе-
35
|
0.6 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
0.2 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
|
0.0 |
|
0.3 |
|
|
|
|
|
|
|
0.0 |
|
|
|
|
|
|
−0.3 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
|
−0.6 |
|
1.8 |
|
|
|
|
|
|
̇ |
1.2 |
|
|
|
|
|
|
0.6 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
|
0.0 |
|
4.0 |
|
|
|
|
|
|
̇ |
2.0 |
|
|
|
|
|
|
0.0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
|
−2.0 |
|
24 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
8 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
|
0 |
Рис. 2.4. Графики зависимости от времени положения тележки , её скорости ̇, угла отклонения маятника , угловой скорости маятника ̇и управления для линейной (красный цвет) и нелинейной (синий цвет) систем, замкнутых линейно-квадратичным регулятором (2.16); начальные условия 0 =
0.0, −0.6, 0.0, 0.0 .
36
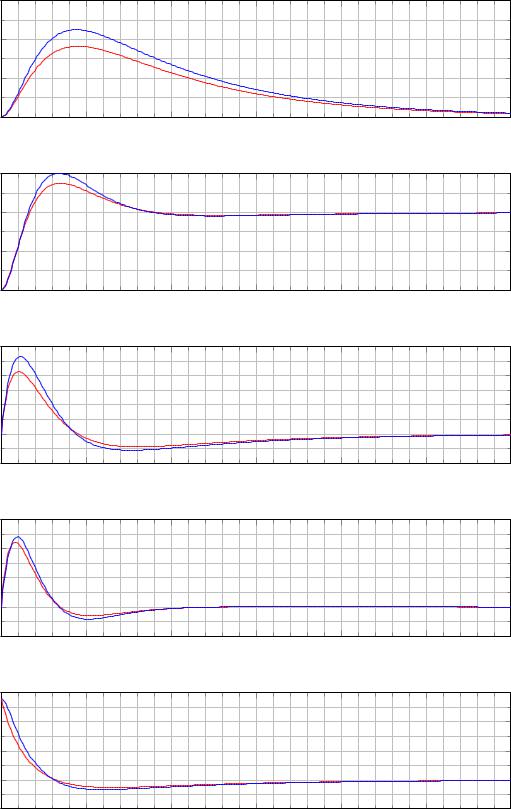
ме (2.5), так и в нелинейной системе (2.4) при использовании регулятора (2.17) приведены на рисунке 2.5. В рассматриваемом случае время установления по компоненте существенно сократилось, но при этом время установления по остальным компонентам стало чуть больше.
Теперь рассмотрим случай, когда в (2.13) учитываются лишь угол отклонения маятника и управление , то есть = diag 0, 1, 0, 0 и= 1. Легко проверить, что = 0, 1, 0, 0 . Однако в этом случае пара матриц ( , ) не является детектируемой. Чтобы показать это, воспользуемся следующей теоремой [].
Теорема 2.2. Пара матриц ( , ) детектируема тогда и только тогда, когда у матрицы не существует собственных чисел , удовлетворяющих условиям
= , |
= 0, |
Re 0. |
Таким образом, для доказательства детектируемости пары ( , ) нужно проверить все правые собственные векторы матрицы на ортогональность матрице и определить знак вещественной части тех собственных чисел, которые соответствуют ортогональным векторам. В рассматриваемом случае из всех собственных векторов
1 |
≈ |
|
0.017 |
, |
2 |
≈ |
|
0.005 |
, |
3 |
= |
1 |
, |
4 ≈ |
−0.001 |
||||||
|
0.089 |
−0.156 |
0 |
−0.155 |
|||||||||||||||||
|
|
|
−0.141 |
|
|
|
|
−0.030 |
|
|
|
|
0 |
|
|
−0.007 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
только |
|
|
−0.986 |
|
|
|
|
|
0.987 |
|
|
|
|
0 |
|
|
−0.988 |
||||
ра |
вектор , соответствующий собственному числу |
|
, удовле- |
||||||||||||||||||
|
|
|
|
3 |
= 0 |
|
|
|
= 0 |
|
|
|
|
мнимой оси, то па- |
|||||||
творяет условию |
|
|
|
|
. Так как |
|
|
|
лежит на |
||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
= 0 |
|
|||||||
( , ) недетектируема. В этом случае линейно-квадратичный регулятор (2.15) не является стабилизирующим. Покажем это. Найдем решение уравнения Риккати
|
0 |
0 |
0 |
|
0 |
|
|
|
|
0 |
116.563 |
−46.032 |
17.0047 |
|
|
||
|
= |
−46.032 |
18.202 |
−6.721 |
|
|
|
|
|
0 |
|
|
|
||||
и вычислим |
0 |
17.004 |
−6.721 |
2.482 |
|
|
: |
|
|
собственные числа матрицы |
= − −1 |
|
|||||
1 ≈ −11.156, |
2 ≈ −6.702, |
3 |
≈ −6.040, |
4 = 0. |
||||
37
|
|
0.6 |
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
||
|
|
0.0 |
0.5 |
1.0 |
|
1.5 |
2.0 |
|
|
||
|
|
0.3 |
|
2.5 |
|||||||
|
|
0.0 |
|
|
|
|
|
|
|
|
|
−0.3 |
|
|
|
|
|
|
|
|
|||
|
−0.6 |
0.5 |
1.0 |
|
1.5 |
2.0 |
|
|
|||
|
|
2.1 |
|
2.5 |
|||||||
̇ |
|
1.4 |
|
|
|
|
|
|
|
|
|
|
0.7 |
|
|
|
|
|
|
|
|
||
|
|
0.0 |
|
|
|
|
|
|
|
|
|
|
−0.7 |
0.5 |
1.0 |
|
1.5 |
2.0 |
|
|
|||
|
|
6.0 |
|
2.5 |
|||||||
̇ |
|
4.0 |
|
|
|
|
|
|
|
|
|
|
2.0 |
|
|
|
|
|
|
|
|
||
|
|
0.0 |
|
|
|
|
|
|
|
|
|
|
−2.0 |
0.5 |
1.0 |
|
1.5 |
2.0 |
|
|
|||
|
|
|
30 |
|
2.5 |
||||||
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
−10 |
|
|
|
|
|
|
|
|||
|
|
|
|
зависимости от времени положения тележки |
, её скоро- |
||||||
Рис. 2.5. Графики |
0.5 |
1.0 |
|
1.5 |
2.0 |
2.5 |
|||||
сти |
|
, угла отклонения маятника |
|
, угловой скорости маятника |
|
и управле- |
|||||
ния |
̇ для линейной (красный цвет) и нелинейной (синий цвет) систем, за- |
||||||||||
мкнутых линейно-квадратичным регулятором (2.17); начальные условия̇ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 = |
|
0.0, −0.6, 0.0, 0.0 . |
|
|
38 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, замкнутая система будет устойчивой по Ляпунову, но не асимптотически устойчивой, следовательно, регулятор
|
−1 |
|
|
̇ |
|
(2.18) |
|
= − |
|
= −38.560 + 15.231 − 5.626 |
̇ . |
||||
|
|
|
не является стабилизирующим. Однако в векторе состояния только компонента с течением времени не стремится к нулю, поэтому задача стабилизации маятника по прежнему имеет корректное решение. На рисунке 2.6 приведены графики переходных процессов и управления в линейной и нелинейной системах при использовании регулятора (2.18).
2.2.3. Синтез модального управления по выходу
Теперь рассмотрим случай неизмеряемого состояния, то есть когда отсутствует полная информация о состоянии системы (2.7). Предположим, что непосредственному наблюдению доступны только положение тележки и угол отклонения маятника . В этом случае измеряемый выход имеет вид:
= , |
= |
1 |
0 |
0 |
0 |
(2.19) |
0 |
1 |
0 |
0 . |
|
Сначала покажем, что задача синтеза стабилизирующего регулятора по выходу вида
= 1 + 2 = Θ , |
Θ = 1, 2 |
(2.20) |
не имеет решения. Отметим, что регулятор (2.20) называется статическим регулятором по выходу и является простейшим с точки зрения реализации, поскольку не требует построения наблюдателя. Параметры обратной связи 1 и 2 находятся таким образом, чтобы матрица замкнутой системы
|
|
|
0 |
0 |
|
|
|
1 |
0 |
|
|
= + Θ = |
|
0 |
|
|
|
0 |
|
||
0 |
|
|
2 |
1 |
||||||
|
|
|
1 |
|
|
|
−10.640 |
|
|
|
|
|
1.397 |
0.776 + 1.397 |
−0.008 |
||||||
|
|
6.046 1 |
45.767 + 6.046 2 |
−46.044 |
−0.496 |
|||||
была устойчивой. Записывая для матрицы |
|
характеристический по- |
||||||||
лином |
|
|
|
|
|
|
|
|
||
( ) = 4 + 11.136 3 |
− (40.879 + 1.397 1 |
+ 6.046 2) 2 − |
|
|||||||
|
|
|
|
− (451.235 + 0.642 1) + 59.248 1 |
||||||
39

|
0.6 |
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
0.0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
0.3 |
|
|||||
|
0.0 |
|
|
|
|
|
|
−0.3 |
|
|
|
|
|
|
|
|
−0.6 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
1.8 |
|
|||||
̇ |
1.2 |
|
|
|
|
|
|
0.6 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
|
0.0 |
4.5 |
|
|
|
|
|
|
3.0 |
|
|
|
|
|
|
̇ 1.5 |
|
|
|
|
|
|
0.0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
−1.5 |
|
24 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
8 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
|
|
|
0 |
Рис. 2.6. Графики зависимости от времени положения тележки , её скорости ̇, угла отклонения маятника , угловой скорости маятника ̇и управления для линейной (красный цвет) и нелинейной (синий цвет) систем, замкнутых линейно-квадратичным регулятором (2.16); начальные условия 0 = 0.0, −0.6, 0.0, 0.0 .
40
