
6822
.pdf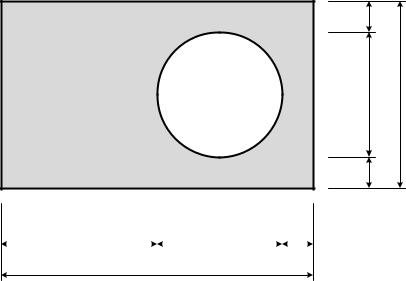
30
A = A1 -A2 = 40a2 - 9a2 = 31a2 ;
5. Определяем координаты центра тяжести всей фигуры и показываем его на рисунке.
|
|
|
|
x A - x A |
|
|
0 × 40a2 -1.5a ×9a2 |
|||||||
x |
C |
= |
|
1 |
1 |
2 |
2 |
= |
|
|
|
= -0.44a; |
||
|
A - A |
|
31a2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
y |
|
= |
|
y A - y |
2 |
A |
|
= |
0 × 40a2 - 2a ×9a |
2 |
= -0.58a; |
|||
C |
|
1 |
1 |
|
2 |
|
|
|
||||||
|
|
A - A |
|
|
31a2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
Задача 1.18. Определение положения центра тяжести Определить положение центра тяжести плоской фигуры, показанной на рис. 1.40.
a
4a 6a
a
5a |
|
4a |
|
a |
||
|
|
|
||||
|
|
|
|
|
|
|
10a
Рис. 1.40
Решение
1.Разбиваем фигуру на простые составляющие (рис. 1.41).
2.Выбираем исходную систему координат xO yO . Для упрощения решения задачи начало исходной системы координат О совместим с центром тяжести первой фигу-
ры и ось x0 направим по оси симметрии. В этом случае неизвестным остается поло-
жение центра тяжести фигуры на этой оси, то есть координата xC .
3. Определяем площади и координаты центров тяжести частей фигуры.
A = 6a ×10a = 60a2 |
; |
x = 0; |
1 |
|
1 |
A2 = π (2a )2 = 12.56a2 ; |
x2 = 2a; |
|
4. Определяем общую площадь фигуры.
A = A1 -A2 = 60a2 -12.56a2 = 47.44a2 ;

|
|
31 |
|
|
yC |
y0 |
|
|
|
|
y1 |
y2 |
|
|
|
|
|
|
a |
|
|
|
|
3a |
|
|
|
|
2a |
C O C |
C |
2 |
x1 = x2 = xC |
|
|
1 |
|
|
|
|
|
|
|
2a |
|
|
|
|
3a |
|
|
|
|
a |
|
xC |
2a |
|
|
5a |
|
4a |
|
a |
|
|
|
||
|
10a |
|
|
|
|
|
Рис. 1.41 |
|
|
5. Определяем координаты центра тяжести всей фигуры и показываем его на рисунке.
x |
|
= |
x A - x A |
= |
0 ×60a2 - 2a ×12.56a2 |
= -0.53a; |
||
C |
1 1 |
2 2 |
|
|||||
A - A |
47.44a2 |
|||||||
|
|
|
|
|||||
|
|
|
1 |
2 |
|
|
|
|
Ответ: (-0,53а;0)

32
ГЛАВА 2. КИНЕМАТИКА
2.1 Кинематика точки
Рассмотрим три способа задания движения точки: 1. Векторный способ задания движения точки
y
M
R
r
j
O |
|
x |
|
R i
R
r - радиус вектор точки М.
R
траекториягодограф радиусвектора r.
Рис.2.1
Закон движения: ! !"#$. Траектория: годограф радиус-вектора.
Скорость: (((!' )*)+! !,.
-! ).(! )/*!.
Ускорение: )+ )+/
2. Координатный способ задания движения точки
01 1"#$
Закон движения: 2 2"#$ .
Траектория: из закона движения надо исключить время – y=f(x).
Скорость: |
'4 |
2, |
|
- Проекции вектора скорости: |
|
||
0'3 |
1, |
|
|
- Модуль вектора скорости: |
' '35 '45 |
||
- Направляющие косинусы: |
64 |
'4 |
⁄' |
063 |
'3 |
⁄' . |
|
Ускорение:
33
0-3 ',3 18
- Проекции вектора ускорения: - ', 28
4 4
- Модуль вектора ускорения: |
- -35 -45 |
|
|
|
||||||||||||
- Направляющие косинусы: |
94 |
-4 |
⁄- |
|
|
|
|
|
||||||||
093 |
-3 |
⁄-. |
|
|
|
|
|
|||||||||
3. Естественный способ задания движения точки |
|
|
|
|||||||||||||
|
|
|
|
|
|
− |
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
M |
|
|
|
|
|
|
|
|
траектория |
|
|
R |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ − единичный вектор касательной |
|
|
|
|
|
R |
|||||||||
|
R |
− единичный вектор нормали |
|
|
|
|
|
R |
v |
|||||||
|
|
|
|
|
|
n |
|
|||||||||
|
n |
|
|
|
|
|
+ |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.2 |
|
|
|
|
|
||
Закон движения: |
: :"#$, |
где s – дуговая координата. |
|
|||||||||||||
Траектория: |
|
|
задана. |
|
|
|
|
|
|
|
|
|
|
|||
Скорость: |
|
'! ';<! |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
'; :,- проекция вектора скорости на касательную. |
||||||||||||
Модуль вектора скорости: |
' |';|. |
|
|
|
|
|
|
|
|
|||||||
Ускорение: |
(((!- -!; -!> |
-;<! ->6(!, |
|
|
|
|
|
|
||||||||
где |
-; |
).? |
:8 |
- касательное ускорение, |
|
|
||||||||||
)+ |
|
|
||||||||||||||
|
-> |
./ |
|
- нормальное ускорение (направлено в сторону вогнутости |
||||||||||||
|
@ |
|
||||||||||||||
траектории), |
A радиус кривизны траектории, B @C – |
кривизна. |
||||||||||||||
Модуль вектора ускорения: - -5 -5
; >
Знак скалярного произведения векторов ускорения и скорости позволяет определить является движение ускоренным или замедленным. При ускоренном движении оно положительно, а при замедленном - отрицательно.
Задача 2.1. Векторный способ задания движения точки
Движение точки задано в векторной форме: (!D E! FGH I J! I K(!. Параллельно какой оси направлено ускорение точки?

34
Решение: |
D(! E! FGH I J! I K |
|
|
|
||
Дифференцируя |
, |
|
находим вектор скорости: |
|||
|
|
(! |
|
|||
|
|
|
, |
|
(! |
|
|
|
(! |
L(! D(! MNF I J! K |
|
||
и вектор ускорения: |
L(! FGH I J! |
|
|
|||
|
, |
. |
|
|
||
Получили, что вектор ускорения параллелен оси y. Ответ: ускорение точки направлено параллельно оси Oy.
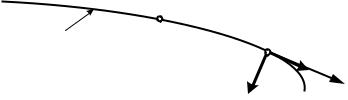
Задача 2.2. Естественный способ задания движения точки Движение точки задано в естественной форме по некоторой заданной траектории.
Закон движения: F I I . Нормальное ускорение равно H см MNHFI. Определить радиус кривизны траектории при t=1с.
− 
траектория
O |
|
|
|
|
|
s |
M |
|
|
|
|
|
|
|
|
|
|
|
|
+
Рис. 2.3
Решение:
Определяем уравнение скорости: LP F, I.
Вычисляем модуль скорости при t=1с: L|IQ | ∙ | мс.
Вычисляем радиус кривизны при t=1с: R LH см .
Ответ: R м.
Задача 2.3. Векторный способ задания движения точки
Движение точки задано в векторной форме: D(! . I (!E . I J!. Определить величину (модуль) ускорения точки при t=t1=2c.
Решение:
Дифференцируя D(! . I (!E . I J! по времени находим вектор скорости:
(!L (!D, . I (!E . I J!
и вектор ускорения: (! (!L, . (!E . I J! .
Подстановкой определяем вектор ускорения при t=t1=2c.
(!|IQ M . (!E . ∙ J! . (!E . J!.

35
Находим модуль вектора ускорения:
√ . . . √ см .
Ответ: . √ см .
Задача 2.4. Координатный способ задания движения точки
Найти траекторию точки М, радиус кривизны траектории, а также скорость и |
||
ускорение в момент времени |
I , |
если движение точки задано уравнениями |
S MNF I м, T FGH I м. |
|
|
Решение
1. Уравнение траектории. Используем тригонометрическое тождество FGH U
MNF U и исключим время из уравнений движения:
"S⁄ $ "T⁄ $ .
Из этого уравнения следует, что траекторией точки является эллипс с полуосями
5 м и 3 м, центр которого находится в начале координат. |
S|IQ 5 м, |
||||||||||
2. Положение точки при |
I |
определим через ее координаты: |
|||||||||
T|IQ 0, откуда следует, что точка М – |
|
крайняя точка эллипса (см. рис.). |
|||||||||
3. Скорость точки найдем по ее проекциям: |
|
|
|||||||||
|
|
LS S, FGH I, |
|
LT T, MNF I. |
|
||||||
При |
I |
LS|IQ , |
LTVIQ м⁄с, |
откуда видно, что вектор скорости |
|||||||
направлен по оси y. |
|
|
|
|
|
|
|
|
|
||
|
L |
|
м⁄с. |
|
|||||||
Модуль скорости равен |
LS LT |
|
|||||||||
4. Ускорение точки тоже определяем по проекциям: |
|
||||||||||
|
S |
L, MNF I, |
|
T |
L, FGH I. |
|
|||||
|
|
S |
|
|
|
|
T |
TVIQ , откуда видно, ускорение |
|||
При |
I |
имеем: S|IQ |
|
м⁄с , |
|||||||
направлено против оси y. |
S W м⁄с . |
|
|||||||||
Модуль ускорения равен |
|
||||||||||
Из рисунка 2.4 видно, что ускорение перпендикулярно скорости, то есть является нормальным ускорением. Касательное ускорение в данный момент времени отсутствует. Убедимся в этом.

36
y |
|
|
|
3 |
|
R |
|
|
|
v |
|
R |
R |
|
|
a |
= an |
5 |
x |
−5 |
|
M
−3
Рис.2.4
Касательное ускорение найдем по формуле :
| P| XLS SYLL T TX .
Нормальное ускорение вычислим как геометрическую разность между полным и
касательным ускорениями:
H P м⁄с .
5. Радиус кривизны траектории найдем из формулы
R LH . м.
Задача решена
Задача 2.5. Координатный способ задания движения точки
В координатной форме задан закон движения груза, сброшенного с самолета:
0S I
T I .
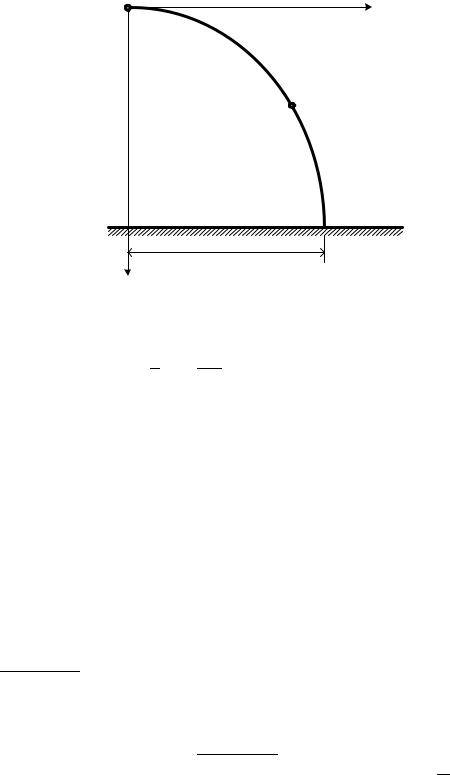
Высота полета самолета равна h=320м. Найти: траекторию груза (точки М), расстояние по горизонтали между точками сброса и падения, скорость и ускорение в точке падения, радиус кривизны в точке падения.
Решение:
1. Определяем траекторию. Для этого исключаем время из закона движения точки М.
I |
S |
, |
откуда |
T I |
I |
|
|
S . |
|
|
|
|
|
||||||
Так как I Z , то |
S Z и T Z . |
T |
|||||||
Следовательно, траекторией является правая ветвь квадратной параболы |
|||||||||
S .
|
37 |
O |
|
|
x |
|
M |
h |
|
y |
480 м |
|
|
|
Рис.2.5 |
2. Определяем положение точки М1 момент времени t1 при y=h=320м.
Так как T I , то I [ M. При этом S I ∙ м.
3. Определяем скорость и ускорение груза в момент падения.
Определяем проекции вектора скорости на координатные оси:
LS S, ,
LT T, I.
Определяем проекции вектора ускорения на координатные оси:
S LS, S8 ,
T LT, T8 .
Вычисляем модуль вектора скорости:
L LS LT "I$ √ I .
При I I M значение скорости будет равно L √ мс. Найдем модуль ускорения: S T √ см .
4. Вычисляем нормальное и касательное ускорения точки, а также радиус кривизны траектории:
|
|
|
|
|
|
|
|
38 |
|
|||||||||||
| P| X\L\IX ] |
|
|
I |
|
] ] |
|
I |
|
], |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
YI |
|
YI |
|
|
|
|
||||||||||||||
H P |
YII |
|
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
YI |
|
R LH " I $ , |
||||||||||||||||||
5. Определяем радиус кривизны траектории : |
||||||||||||||||||||
откуда получаем радиус кривизны в момент падения при I M: |
||||||||||||||||||||
L |
|
|
|
|
|
|
|
, м. |
|
|
|
|
||||||||
R H |
" |
$ |
|
|
|
|
|
|||||||||||||
Ответ: S |
м, L мс , |
м |
, R , м. |
|||||||||||||||||
с |
||||||||||||||||||||
Задача 2.6. Естественный способ задания движения точки
Материальная точка М движется по окружности, которая имеет радиус R=2м. В начальный момент времени точка находится в положении О (начало отсчета дуговой координаты). Задан закон движения материальной точки М в естественной форме _ `I ` I . Положительное направление отсчета принято по часовой стрелке.
В момент времени t=2с найти: положение точки М (точку М1); вектор скорости (!L; векторы полных, касательных и нормальных ускорений: (!, (!P, (!H.
Определить является движение в данный момент времени ускоренным или замедленным.
Решение
1. Покажем положение точки М на траектории в произвольный момент времени t (рис.2.6).
Покажем на рисунке угол , который соответствует дуговой координате s.

39
|
|
R |
|
|
|
τ − единичныйвектор, |
|
R |
|
направленный в положительном |
|
|
|
||
− |
|
направлении дуговой координаты |
|
C |
O |
О − начало отсчета |
|
|
R |
дуговой координаты |
|
α |
τ |
||
|
|||
+ |
|
|
|
M |
|
S − дуговая |
|
|
|
||
R |
|
координата |
|
τ |
|
|
Рис.2.6
2. Определяем положение точки М при t=2c (точку М1).
Из геометрии известно соотношение между центральным углом окружности и длиной соответствующей дуги: _ U.
Определим дуговую координату для момента времени t=2c.
F|IQ M ` ∙ ` ∙ ` ` `.
Это значение дуговой координаты соответствует центральному углу
U F ` .
Показываем точку М1 на рисунке.
R |
|
|
R |
R |
|
|
aτ |
M1 τ |
v |
|
|||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
aτ ×vτ < 0 - движение |
R |
|
|
R |
|
||
|
|
|||||
|
|
an |
|
|
||
a |
|
|
− |
замедленное |
||
|
|
|
|
|
|
|
3π |
|
|
C |
|
O |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
Рис.2.7
3. Определяем скорость точки.
Определяем проекцию скорости на единичный вектор касательной:
