
6067
.pdf
-48-
|
|
∑n [(mi -1)× Si2 ] |
|
|
|
||||||
S 2 = |
i =1 |
|
|
|
. |
|
|
(72) |
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
K |
|
|
|
|||
|
1 |
|
|
|
n |
1 |
|
|
1 |
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
С = 1 + |
3(n -1) |
× |
(m -1) - |
K . |
(73) |
||||||
|
|
|
|
i =1 |
i |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Следует отметить, что для надежной оценки число параллельных измерений должно быть не менее mi = 6 . Критерий Бартлетта приближенно распределен как
χ2 -распределение (критерий Пирсона) с числом степеней свободы f = (n − 1). Если
χ 2 |
< B < χ 2 |
, то с принятой доверительной вероятностью можно утверждать, |
α 2 |
(1−α 2) |
|
что между сравниваемыми дисперсиями статистически значимых отличий не обна-
ружено, т.е. справедлива нуль-гипотеза Н |
0 |
( S 2 ): S 2 |
= S |
2 |
= ... = S |
2 . |
||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
n |
|
Если подтверждена гипотеза Н |
0 |
( S 2 ): S 2 |
= S |
2 |
= ... = S |
2 |
, |
то следующим шагом |
||||
|
|
|
1 |
|
2 |
|
|
|
n |
|
|
|
является проверка нуль-гипотезы о статистическом равенстве средних результатов выборок ( Н0( Х ): Х1 = Х 2 = ... = Х n ) методом однофакторного дисперсионного анали-
за. Логическим основанием этого метода является то, что если не отвергается гипоте-
за о равенстве внутригрупповой (Sвг2 ) и межгрупповой (Sмг2 ) дисперсий, то можно
считать, что при переходе от группы к группе нет какого-либо неслучайного смеще-
ния (т.е. нет какого-либо влияния технологического |
фактора на величину |
измерения |
|||||||||||||
изучаемой величины) и, следовательно, допускается |
гипотеза о статистическом ра- |
||||||||||||||
венстве средних результатов в группах. |
В этом случае гипотеза о статистическом ра- |
||||||||||||||
венстве n |
средних проверяется через гипотезу о статистическом равенстве внутри- |
||||||||||||||
групповой и межгрупповой дисперсий |
(H0 (S 2 ): Sвг2 |
= S мг2 ) по критерию |
Фишера, |
||||||||||||
расчетное значение которого определяется по формуле: |
|
||||||||||||||
|
|
|
|
F |
|
|
= |
Sмг2 |
|
, |
|
|
|
(74) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
расч |
|
S 2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
вг |
|
|
|
|
|
||
где |
S 2 |
и |
S 2 |
- межгрупповая и внутригрупповая дисперсии, вычисляемые по |
|||||||||||
|
мг |
|
вг |
|
|
|
|
|
|
|
|
|
|
|
|
формулам (75) |
и (76) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
∑ (Х |
i − Х) |
|
|
|||||
|
|
|
|
S 2 |
= |
i=1 |
|
|
|
, |
(75) |
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
мг |
|
|
(n −1) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
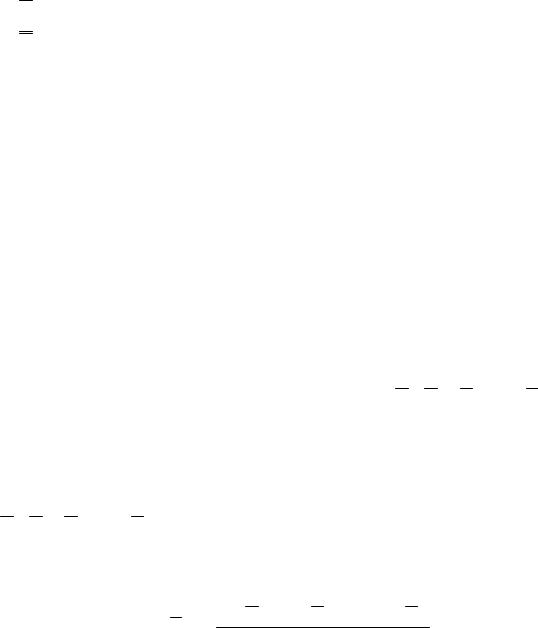
-49-
|
n |
|
|
|
|
∑ Si2 |
|
|
|
Sвг2 = |
i=1 |
, |
(76) |
|
n |
||||
|
|
|
где n - число групп испытаний;
Хi - среднее арифметическое каждой группы измерений;
Х- среднее арифметическое по всем группам измерений, определяемое по
формуле (77);
Si2 - дисперсия каждой группы измерений.
|
|
n |
|
|
|
|
|
|
|
∑ |
Х |
i |
|
||
|
= |
i =1 |
. |
(77) |
|||
|
|||||||
Х |
|||||||
|
|||||||
|
|
n |
|
||||
Табличное значение критерия Фишера в этом случае определяется при задан-
ном уровне значимости α (обычно α = 0,05) и числе степеней свободы числителя
fч = (n -1) и |
знаменателя |
fзнам = m ×(n -1). Если Fрасч £ Fтабл , |
то с принятой до- |
верительной |
вероятностью |
принимается гипотеза H 0 (S 2 ): Sвг2 |
= Sмг2 . Следователь- |
но, с принятой доверительной вероятностью можно утверждать, |
что между сравни- |
||
ваемыми средними результатами всех групп испытаний статистически значимых различий не обнаружено (т.е. справедлива гипотеза Н0( Х ): Х1 = Х 2 = ... = Х n ), коле-
бания средних результатов от группы к группе обусловлены только ошибками изме-
рений и действием неучтенных факторов, но не влиянием технологических факторов.
Если последовательно подтверждены гипотезы Н |
0 |
(S |
2 ):S 2 |
= S |
2 |
= ... = S |
2 |
и |
|
|
1 |
|
2 |
|
n |
|
Н0( Х ): Х1 = Х 2 = ... = Х n , то все выборочные совокупности можно объединить в од-
ну выборку. Обобщенные статистические характеристики вычисляются по форму-
лам
Хоб = m1 × Х1 + m2 × Х 2 + ... + mn × Х n , m1 + m2 + ... + mn
S |
2 |
(m |
-1)× S |
2 |
+ (m |
2 |
-1)× S |
2 |
+ ... + (m |
n |
-1)× S |
2 |
|
1 |
1 |
|
|
2 |
|
|
n . |
||||||
|
об |
|
|
(m1 + m2 + ... + mn ) - n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
(78)
(79)

-50-
3.Построение эмпирических формул методом наименьших квадратов
3.1.Общие положения
В технологии бетона издавна стремились обобщить опыт в виде математиче-
ских моделей, отражающих те или иные стороны наблюдаемого явления. Уже в пер-
вых работах (И.Г. Малюга, Р. Фере и др.) сложились три направления количествен-
ного описания закономерностей технологии бетона, которые получили развитие и в дальнейших исследованиях:
а) построение графиков Y = f ( X ) при прочих равных условиях (например,
построение графика зависимости прочности бетона от цементно-водного отношения);
б) описание таких графиков эмпирическими формулами, например описание прочности бетона известной формулой Боломея Rб = ARц (Ц В± С);
В± С);
в) построение аналитических формул на основе некоторых физико-химических представлений (сначала в алгебраической, а позже в дифференциальной форме).
В зависимости от исходной информации можно получить модели, описываю-
щие с известной точностью определенных процесс или явление, как например, обоб-
щенные модели прочности бетона (типа формулы Боломея с коэффициентами,
усредненными по результатам испытаний бетона на разных материалах), либо част-
ные модели, описывающие данный процесс или явление в конкретных условиях, на-
пример модель прочности бетона для определенных видов материалов, используемых на данной стройке.
Наибольшую сложность при построении любой математической модели пред-
ставляет решение вопроса о выборе формы связи (линейная или нелинейная) между переменными. Однако ряд трудностей моделирования можно исключить, если при-
менить некоторые ограничения - модель должна быть максимально проста и как можно точнее описывать поведение системы в конкретной ситуации.
В этом случае отпадает необходимость поиска в каждой задаче специфических математических форм связи между аргументом (фактором) Хi (при числе факторов
К) и функцией (параметром выхода) Y . Если самая простая модель окажется недо-
-51-
статочно точной, ее можно усложнять. Воспользовавшись тем, что любую непрерыв-
ную функцию можно разложить в ряд Тейлора, который преобразуется в степенной ряд, начальную модель поведения системы удобно представить в виде полинома т-й
степени
|
|
= β |
|
К |
|
К |
|
|
К |
|
|
|
|
|
+ ... |
|
Y |
0 |
+ ∑ β Х |
i |
+ ∑ β Х 2 |
+ ∑ β |
ij |
Х |
i |
Х |
j |
(80) |
|||||
Q |
|
i |
ii |
i |
|
i=1 |
|
|
|
|
||||||
|
|
|
|
i=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
При проведении вычислительной процедуры необходимо по результатам ис- |
||||||||||||||||
следования системы как можно точнее найти оценки |
коэффициентов b → β и полу- |
|||||||||||||||
чить расчетную модель поведения системы |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
К |
|
К |
2 |
|
К |
|
|
|
|
|
|
|
Y = b |
+ ∑ b Х |
i |
+ ∑ b Х |
+ |
∑ b |
Х |
i |
Х |
j |
+ ... |
(81) |
|||||
|
|
|
0 |
i |
ii |
i |
|
i=1 |
ij |
|
|
|
|
|||
|
|
|
|
i=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j ¹1 |
|
|
|
|
|
|
|
Вычислительная процедура определения коэффициентов b0, bi , bii , bij ... мо-
дели (87) построена на основе метода наименьших квадратов. Его сущность разъясня-
ется ниже на примере вычисления коэффициентов линейной, а затем и нелинейной
модели.
3.2. Вычисление коэффициентов однофакторной линейной модели
Пусть при изучении влияния фактора Х1 |
на выход системы Y, получили табли- |
||||
цу 4 измерений значений фактора и параметра выхода. |
|
||||
|
|
|
|
|
Таблица 4 |
Таблица значений фактора и параметра выхода |
|
||||
Номер |
Значение фактора Х1 |
Значение параметра выхода Y |
|||
опыта |
|
|
|
|
|
1 |
Х11 |
|
y1 |
||
2 |
Х12 |
|
y2 |
||
…. |
…. |
|
… |
||
u |
Х1U |
|
y U |
||
….. |
… |
|
… |
||
N |
Х1N |
|
y1N |
||
Если предположить, что Y находится в линейной |
зависимости от Х1, то по- |
||||
ведение системы можно описать моделью: |
|
|
|||
|
|
|
= а + b × X . |
(82) |
|
|
Y |
||||

-52-
Необходимо подобрать такие значения а и b или так провести прямую (рис. 7),
чтобы модель (91) наиболее полно соответствовала данным табл. 4. Провести пря-
мую через все точки с координатами {Х1u , Yu} (т.е. через экспериментально полу-
ченные точки), как правило, невозможно. Это объясняется тем, что или измерения
Х1u и Yu весьма точны, но предположение о линейном влиянии X1 на Y несовер-
шенно, или влияние X1 на Y действительно линейно, но значения Yu измерены со
значительной погрешностью, или наряду с несовершенством гипотезы о линейном влиянии X1 на Y существует еще и погрешность измерений Yu (наиболее часто встречающийся в технологии строительных материалов случай).
Следовательно, всегда между наблюдаемым значением Yu и рассчитанным по модели значением Y u будет разница u :
|
|
Du = Yu - Y u . |
(83) |
||
|
|
|
|
|
Y=1+2X |
Рис. 7. |
Экспериментальные точки параметра выхода и линия регрессии, по- |
||||
строенная по модели Y = а + b × X =1 + 2 × X : |
▪ - значения параметра выхода, полу- |
||||
ченные в ходе эксперимента; |
— ■— ■— |
- |
значения параметра выхода, получен- |
||
ные по модели (91). |
|
|
|
|
|
-53-
Таким образом, главным вопросом при решении поставленной задачи является
N
минимизация суммы отклонений ∑ u . Однако из математики известно, что про- u =1
стейшая вычислительная процедура получается в том случае, если минимизируется
N |
|
|
|
|
|
|
N |
2u : |
не сумма отклонений ∑ |
u , а сумма квадратов отклонений |
∑ |
||||||
u =1 |
|
|
|
|
|
|
u =1 |
|
|
N |
N |
|
|
||||
|
∑ D2u = ∑(Yu - |
|
u )2 ® min . |
|
(84) |
|||
|
Y |
|
||||||
|
u =1 |
u =1 |
|
|
||||
|
|
|
||||||
При подстановке в (93) значений Y u по модели (91) для каждого u-го опыта |
||||||||
получим: |
|
|
|
|
|
|
|
|
N |
N |
|
|
|
|
|
|
|
∑D2u = ∑(Yu - а - b × Х1u )2 ® min . |
|
(85) |
||||||
u =1 |
u =1 |
|
|
|
|
|
|
|
Для нахождения минимума функции необходимо приравнять нулю частные производные по всем неизвестным (их два – а и b). После дифференцирования име-
ем так называемую систему нормальных уравнений:
N |
- а - b × Х1u ) = 0 |
|
|
|||
- 2 ∑ (Yu |
|
|
||||
u =1 |
|
|
|
|
|
(86) |
N |
|
|
|
|
. |
|
- а - b × Х |
|
)× Х |
|
= 0 |
|
|
- 2 ∑ (Y |
1u |
1u |
|
|||
u |
|
|
|
|
||
u =1 |
|
|
|
|
|
|
Проведя преобразования, получим:
а × N + b × |
N |
|
N |
|
|
|
|
|
||
∑ X1u = |
∑Yu |
|
|
|
|
|||||
|
|
|
u =1 |
|
u =1 |
|
|
|
|
(87) |
|
N |
|
|
N |
|
|
N |
|
. |
|
а × |
|
+ b × |
|
= |
|
|
|
|||
∑ X |
1u |
∑ X 2 |
∑ X |
Y |
|
|||||
|
u =1 |
|
u =1 |
1u |
|
u =1 |
1u u |
|
||
|
|
|
|
|
|
|
|
|||
Решая совместно оба уравнения относительно b0 и b1, получим расчетные формулы:

-54-
|
N |
N |
|
2 |
- |
N |
|
|
× |
N |
|
|
|
|
|
|
|
||
|
∑Y |
× ∑ |
X |
∑ X |
1u |
∑ X |
1u |
Y |
|
||||||||||
|
|
u |
u =1 |
1u |
|
u =1 |
|
u =1 |
|
|
u |
|
|||||||
а = |
u =1 |
|
|
|
|
|
|
|
|
|
, |
(88) |
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
N |
2 |
|
|
N |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
N × ∑ X1u - |
∑ X1u |
|
|
|
|
|
|
|
|||||||||
|
|
|
u =1 |
|
|
|
u =1 |
|
|
|
|
|
|
|
|
|
|||
|
|
N × |
N |
|
|
|
- |
N |
|
|
|
N |
|
|
|
|
|
|
|
|
|
∑ X Y |
|
∑Y × |
∑ X |
|
|
|
|
|
|
|
|||||||
b = |
|
u =1 |
1u u |
|
|
u =1 u |
u =1 |
1u |
. |
|
|
(89) |
|||||||
|
N |
|
2 |
|
|
|
N |
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N × ∑ X1u |
|
|
∑ X1u |
|
|
|
|
|
|
|
|||||||
|
|
|
u =1 |
|
|
|
u =1 |
|
|
|
|
|
|
|
|
|
|||
Пример 6. Пользуясь методом наименьших квадратов определить коэффици-
енты математической модели, описывающей зависимость прочности тяжелого бетона от цементноводного (водоцементного) отношения Rб = ARц (Ц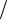 В ± С). При прове-
В ± С). При прове-
дении эксперимента использованы портландцемент с активностью 40,8 МПа, гранит-
ный мытый щебень и песок средней крупности. Результаты испытаний девяти соста-
вов приведены в табл. 5.
Таблица 5
Результаты испытаний бетонных образцов
Наименование |
|
|
|
№ |
состава |
|
|
|
|||
показателя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
|
Ц В |
2,5 |
2,3 |
2,1 |
1,9 |
1,7 |
1,5 |
1,3 |
1,15 |
1,0 |
|
|
|
44,9 |
40,0 |
36,1 |
31,4 |
26,9 |
22,0 |
18,0 |
14,8 |
11,4 |
|
Rб МПа |
||||||||||
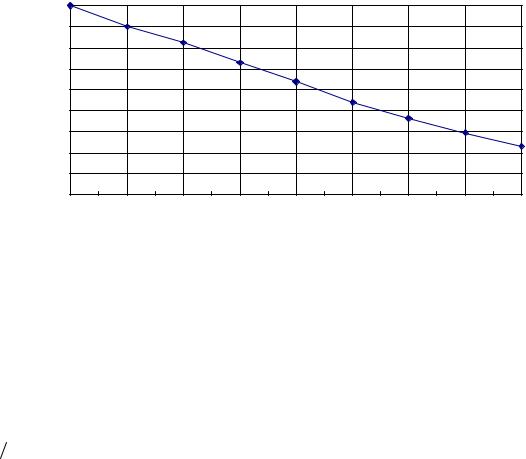
Построим график изменения прочности в зависимости от цементноводного от-
ношения (рис. 8). Он наглядно свидетельствует, что экспериментальные данные мо-
гут быть с достаточной точностью аппроксимированы линейной зависимостью.
Поскольку эксперимент проводился при постоянной активности цемента и дру-
гих постоянных факторах (например, качество крупного и мелкого заполнителя и
т.д.), влияющих на прочность бетона, то за Х принимаем цементноводное отноше-
ние - Ц В. Так как прочность бетона зависит и от активности цемента введём до-
полнительное обозначение Y = Rб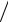 Rц .
Rц .
|
|
|
|
|
-55- |
|
|
|
|
|
|
45 |
44,9 |
|
|
|
|
|
|
|
|
|
40 |
|
40 |
36,1 |
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
||
|
|
|
|
31,4 |
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26,9 |
|
|
|
||
|
25 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
22 |
|
|
|
|
|
20 |
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
15 |
|
|
|
|
|
|
14,8 |
||
|
|
|
|
|
|
|
|
|||
|
10 |
|
|
|
|
|
|
|
|
11,4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2,5 |
2,3 |
2,1 |
1,9 |
1,7 |
1,5 |
1,3 |
1,15 |
1 |
Рис. |
8. |
|
Изменение |
|
прочности |
|
бетона |
от |
цементноводного |
|
отношения |
|
|
|
|
|
|
|
|
|
|
После преобразования значения параметра выхода Y приведено в табл. 6. |
||||||||||
|
|
|
|
|
|
|
|
|
|
Таблица 6 |
Значения параметра выхода после проведения преобразований
Наименование |
|
|
|
№ |
состава |
|
|
|
|
показателя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Ц В |
2,5 |
2,3 |
2,1 |
1,9 |
1,7 |
1,5 |
1,3 |
1,15 |
1,0 |
Y |
1,103 |
0,968 |
0,895 |
0,748 |
0,674 |
0,527 |
0,512 |
0,343 |
0,294 |
Для облегчения вычисления коэффициентов математической модели (неизвестных коэффициентов в формуле зависимости прочности бетона от цементноводного отношения) составим таблицу расчётных величин (табл. 7).
Таблица 7
Расчетные величины для вычисления коэффициентов модели
№ п/п |
Х |
Y |
Х2 |
Х·Y |
1 |
2,5 |
1,100 |
6,25 |
2,7500 |
2 |
2,3 |
0,980 |
5,29 |
2,1850 |
3 |
2,1 |
0,885 |
4,41 |
1,8585 |
4 |
1,9 |
0,770 |
3,61 |
1,4630 |
5 |
1,7 |
0,660 |
2,89 |
1,1220 |
6 |
1,5 |
0,539 |
2,25 |
0,8085 |
7 |
1,3 |
0,440 |
1,69 |
0,5720 |
8 |
1,15 |
0,363 |
1,3225 |
0,4175 |
9 |
1,0 |
0,279 |
1,0 |
0,2790 |
Σ |
15,45 |
6,016 |
28,7125 |
11,4555 |
-56-
|
N |
N |
N |
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑Yu × ∑ X12u - ∑ X1u × ∑ X1uYu |
|
|
6,016× 28,7125-15,45×11,4555 |
|
|||||||||||||||||||||
а = |
u=1 |
u=1 |
u=1 |
|
|
|
|
|
u=1 |
|
|
= |
|
= - 0,216. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
N |
|
N |
|
|
|
|
|
|
|
|
|
9 × 28,7125-15,452 |
|
|
|||||||||
|
|
|
2 |
|
∑ X1u |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
N × ∑ X1u - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
u=1 |
|
u=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
N |
|
- |
|
N |
|
|
× |
N |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
N × ∑ X Y |
|
∑Y |
|
|
∑ X |
|
|
|
|
9 ×11,4555 - 6,016 ×15,45 |
|
|
||||||||||||
|
b = |
|
u =1 1u u |
|
|
u =1 u |
u =1 1u |
|
= |
= 0,515 . |
||||||||||||||||
|
|
N |
2 |
|
|
|
N |
|
|
|
2 |
|
|
9 × 28,7125 -15,452 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
N × ∑ |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
X1u |
|
∑ X1u |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
u =1 |
|
|
|
u =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, |
уравнение принимает вид: |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Y= |
-0,216+0,515·Х , |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
или |
|
|
|
|
|
|
Rб |
|
|
= -0,216 + 0,515 × Х , |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Rц |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
б = R (-0,216 + 0,515 × |
Ц |
) , |
|
|
|||||||||||||||
|
|
|
|
|
|
R |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ц |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Rб = 0,515 × R |
|
|
|
- 0,42 , |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
В |
|
|
|
|
|||||
что достаточно близко совпадает с общепринятой формулой Боломея-Скрамтаева.
3.3. Вычисление коэффициентов однофакторной нелинейной модели
Линейная зависимость между переменными является наиболее простой. Если зависимость между переменными Y и Xi не является линейной, то для упрощения вычислений можно применить метод линеаризации (выравнивания). Для этого необ-
ходимо подобрать новые переменные U=f(x, y) и V=f(x, y) так, чтобы зависимость между V и U была линейной.
В качестве примера рассмотрим вычисление коэффициентов a и b показа-
тельной однофакторной модели
Для выравнивания (линеаризации) показательной зависимости вида Y = a × ( Х )b
необходимо провести логарифмирование, а затем ввести новые переменные и обозна-
чения:
logY = log a + b × log X , |
(90) |
V = ln Y , U = log X , A = log a, В = b . |
(91) |

-57- |
|
В результате таких действий получаем линейное уравнение: |
|
V = A + B ×U , |
(92) |
коэффициенты A и B которого можно определить, используя методику, разобранную
в п. 3.2. Для перехода к первоначальному уравнению необходим пересчёт коэффици-
ентов - в данном случае а = 10А и b = В.
|
Оценить качество аппроксимации принятым уравнением можно, как это реко- |
|||||||
мендуется в [3], сопоставлением остаточной дисперсии |
|
S 2 |
, которую можно вычис- |
|||||
|
|
|
|
|
|
|
ост |
|
лить по формуле |
|
|
|
|||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∑ (yi - yi )2 |
|
|
|
|||
|
Sост2 = |
i =1 |
|
, |
|
(93) |
||
|
n - l |
|
||||||
|
|
|
|
|
||||
где |
yi - экспериментальное значение функции в каждом конкретном опыте; |
|||||||
yi - значение функции, рассчитанное по полученному уравнению для каждо-
го опыта;
n - количество экспериментальных точек, в которых получены значения функции;
l - количество коэффициентов в полученном уравнении.
Чем меньше остаточная дисперсия Sост2 , тем выше качество аппроксимации,
т.е. тем лучше соответствует экспериментальным данным линия регрессии, получен-
ная по уравнению. С.Л.Ахназарова и В.В.Кафаров [3] рекомендуют оценивать качест-
во аппроксимации по критерию Фишера, расчётное значение которого можно опреде-
лить по формуле
|
|
|
|
|
(n - l )× ∑n (yi - |
|
|
)2 |
|
|
||
|
|
|
2 |
|
y |
|
|
|||||
|
|
Fр = |
S y |
= |
i =1 |
|
, |
(94) |
||||
|
|
2 |
n |
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
Sост |
|
(n -1)× ∑ (yi - yi |
) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
||||
|
|
|
|
|||||||||
где |
y - среднее значение функции по всем имеющимся опытам. |
|
||||||||||
