6067

-10-

Распределение непрерывной случайной величины нельзя задавать при помощи вероятностей отдельных значений. Число значений так велико, что для большинства из них вероятность принять эти значения равна 0, т. е. событие может произойти, а

вероятность его равна 0. Для непрерывных случайных величин изучается вероят-

ность того, что в результате опыта значение случайной величины попадет

внекоторую заранее намеченную совокупность чисел. Удобно пользоваться

В виде функции распределения можно задать распределение как непрерывной,

так и дискретной случайной величины. Можно доказать, что F(x) есть неубывающая

Рис. 2. Функция распределения непрерывной случайной величины (а) и

дискретной случайной величины (б)

-11-

Функция распределения дискретной случайной величины всегда есть разрыв-

ная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений

(рис. 2, б). Сумма всех скачков равна 1.

Для непрерывной случайной величины наиболее часто употребляется произ-

водная функции распределения — плотность распределения вероятности случайной

величины X. Если F(x) непрерывна и дифференцируема, то

Рис. 3. Плотность распределения вероятностей непрерывной случайной величи-

ны

Площадь, ограниченная осью Х, прямыми Х = х1 и Х = х2 и кривой плотности распределения, равна вероятности того, что случайная величина примет значения из

интервала от х1 до х2:

в частности

-12-

Отсюда же выводится еще одно важное свойство плотности распределения

-∞

так как попадание случайной величины в интервал -∞ < Х < +∞ есть достоверное событие.

1.6. Числовые характеристики случайной величины

Вместо задания случайной величины в виде законов распределения вероятно-

стей в прикладных задачах ее часто определяют при помощи числовых характери-

стик – вещественных чисел, выражающих характерные особенности случайной ве-

личины, называемых моментами случайной величины. Различают начальные и цен-

тральные моменты случайной величины.

Начальный момент k-го порядка определяется формулой:

Начальный момент первого порядка (при k=1) называется математическим ожиданием (средним значением) случайной величины. Математическое ожидание обозначается М[X] и может быть определено по формулам:

−∞

Чаще, чем начальные моменты, применяются центральные моменты. Централь-

ный момент k-го порядка обозначается μк и может быть определен по формулам:

-13-

Первый центральный момент всегда равен 0. Второй центральный момент на-

зывается дисперсией. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания,

т.е.

Дисперсия является мерой рассеяния случайной величины вокруг математиче-

ского ожидания. Легко заметить, что единицы измерения дисперсии будут равны

квадрату единиц измерения случайной величины, что представляет существенные

неудобства при оценке рассеяния. Корень квадратный из второго центрального

момента называется средним квадратическим отклонением. Единицы измерения среднего квадратичного отклонения совпадают с единицами измерения случайной ве-

личины. Среднее квадратичное отклонение определяется по формуле

Третий центральный момент, разделенный на σ3х , называется коэффициентом асимметрии:

Коэффициент асимметрии отражает скошенность кривой распределения.

-14-

Величина

ния.

На рис. 4 приведены примеры плотностей распределений с не нулевыми зна-

чениями коэффициентов асимметрии и эксцесса. Для сравнения штриховой линией изображена кривая с теми же математическим ожиданием М[X] и дисперсией D[Х],

но с нулевыми значениями коэффициентов асимметрии и эксцесса.

γ2< 0

Рис. 4. Плотность распределений с ненулевыми коэффициентами асимметрии и эксцесса

1.7. Нормальное распределение

Одним из наиболее часто встречающихся распределений является нормальное распределение. Нормальное распределение занимает особое положение среди других распределений, поскольку нормальный закон распределения является предельным за

-15-

коном, к которому приближаются другие законы распределения. Нормальный закон распределения широко используется при обработке результатов наблюдений.

Случайная величина Х называется распределенной по нормальному закону,

если ее плотность распределения:

Изменение параметров М[Х] и σх на вид нормальной кривой влияет следующим образом. При изменении параметра М[Х] (математического ожидания) форма нор-

мальной кривой не изменится, а график сдвигается влево или вправо. При увеличении

σх островершинность кривой уменьшается и она растягивается вдоль оси ОХ

(рис. 5). При этом площадь, ограниченная кривой и осью ОХ, остается постоян-

ной и равна 1.

Использование формул плотности распределения в практике существенно уп-

рощается, если перейти от нормального распределения с произвольными параметра-

ми М[Х] и σх к нормированному распределению с параметрами М[Х] = 0 ; σх = 1.

называется нормировкой. Нормальное распределение нормированной случайной величины называется стандартным.

Плотность такого распределения имеет вид:

а функция распределения:

-16-

Рис. 5. График плотности нормального распределения: 1 – график плотности нормального распределения при среднеквадратичном отклонении σ1 ; 2 – то же при

σ2 .

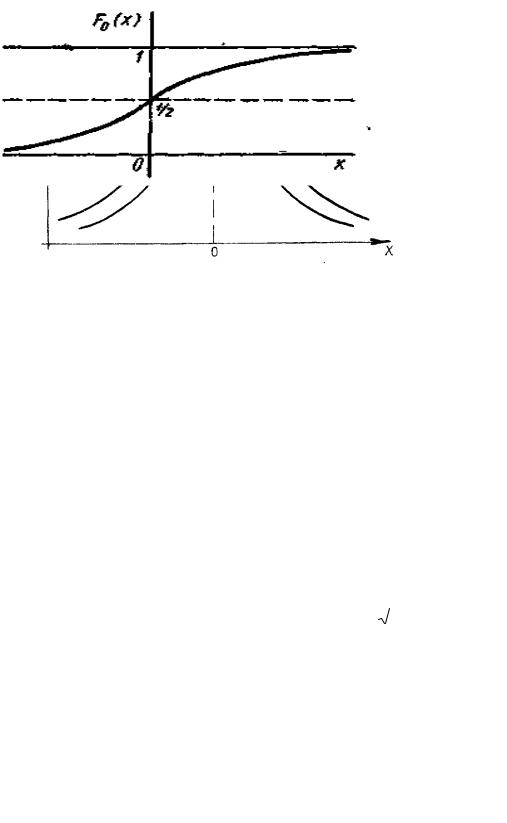
Рис. 6. График функции F0 (x) стандартного нормального распределения

-17-

Значения функции Лапласа, выраженной формулой (33), приведены в прило-

Поэтому таблицы значений Ф(х) составлены лишь для х > 0.

Для нормированной случайной величины, учитывая (31) и (32), имеем

Во многих практических задачах х1 и х2 симметричны относительно матема-

тического ожидания, в частности в задаче об абсолютном отклонении. Абсолютным отклонением называется величина

Требуется найти вероятность того, что абсолютное отклонение случайной величины не превзойдет некоторого заданного числа ε :

-18-

Таким образом, отклонения больше, чем утроенный стандарт (среднеквадрати-

ческое отклонение), практически невозможны.

Отсюда можно сформулировать правило 3σ: если случайная величина распре-

делена по нормальному закону, то отклонения этой величины от ее математическо-

го ожидания по абсолютной величине не превосходят утроенного среднеквадратиче-

ского отклонения.

С помощью функции Лапласа можно решать практические задачи.

Пример 2. Цех по производству железобетонных изделий выпускает плиты перекрытий, изготавливаемых с применением бетона класса В15. При контроле

прочности бетона конструкций получена средняя прочность Х = М( Х ) = 19,3 МПа,

при среднем квадратичном отклонении σ=2,457 МПа.

Определить вероятность появления при испытаниях значений прочности менее

15 МПа.

Решим эту задачу путем вычитания из площади под кривой нормального рас-

ского ожидания (средней прочности Х = М ( Х ) = 19,3 МПа), равняется половине всей площади, т.е F(Х3)= - 0,5 (знак минус указывает на то, что площадь находится слева от математического ожидания).

Находим Z, при Х2=15,0 МПа и Х3=19,3 МПа:

Z = Х2 − М ( Х ) = 15,0 − 19,3 = −1,75 σ 2,457

Площадь под кривой нормального распределения от Х2=15,0 МПа до

Х3= Х = М ( Х ) = 19,3 МПа при этом по приложению 2 равна –0,4599.

Площадь под кривой нормального распределения от Х1= - ∞ до Х2=15,0 МПа

(вероятность попадания значений прочности в интервал от - ∞ до 15,0 МПа) будет равна –0,5-(-0,4599) = -0,0401.

Т.о., вероятность появления значений прочности бетона менее 15,0 МПа равна

0,0401, что соответствует определению класса бетона.

-19-

2.Элементы математической статистики

2.1.Задачи математической статистики. Краткая историческая справка

Установление закономерностей, которым подчинены массовые случайные яв-

ления, основано на изучении методами теории вероятностей статистических данных -

результатов наблюдений. Перед математической статистикой стоит несколько задач,

среди которых можно отметить следующие:

¾указание способов сбора и группировки статистических сведений, полу-

ченных в результате наблюдений или в результате специально поставленных экспе-

риментов;

¾разработка методов анализа статистических данных в зависимости от це-

лей исследования:

а) оценка неизвестной вероятности события; оценка неизвестной функции рас-

пределения; оценка параметров распределения, вид которого неизвестен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.;

б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого неизвестен.

Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование экспери-

мента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности.

Таким образом, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Математическая статистика возникла (XVII в.) и развивалась параллельно с теорией вероятностей. Дальнейшее развитие математической статистики (вторая по-

ловина XIX - начало XX в.) обязано, в первую очередь, П.Л.Чебышеву,

А.А.Маркову, А.М.Ляпунову, а также К.Гауссу, А.Кетле, К.Пирсону и др.

В XX в. наиболее существенный вклад в математическую статистику был сде-

лан советскими математиками (В.И.Романовский, А.Н.Колмогоров, Н.В.Смирнов). а

также английскими учеными (Стьюдент, Р.Фишер, Э.Пирсон) и американскими

(Ю.Нейман, А.Вальд).