Выводы по главе

В данной главе была рассмотрена модель колонии, характеристика ее отдельных элементов и их связей друг с другом. Также составлены формулы реакций для получения различного вида сырья с учетом специальностей, типов местности и видов построек.

Глава 3. Алгоритмы и программная часть.

3.1. Дерево достижимости.

3.1.1.Общее описание.

Для анализа сети Петри необходимо построить дерево достижимости.

Дерево достижимости – это ориентированное корневое дерево, вершинам которого соответствуют возможные маркировки, а дугам – переходы.

Корневая вершина – первоначальная маркировка. Из каждой вершины исходят дуги соответствующие разрешённым переходам. Граничной вершиной называется вершина, построенная на очередном шаге алгоритма. Если у некоторой граничной маркировки нет исходящей дуги – эта маркировка(вершина) называется терминальной.

Если какая-либо граничная вершина имеет маркировку уже существующую в дереве, она называется дублирующей.

Внутренняя вершина – та, которая не является ни граничной, ни терминальной, ни дублирующей.

Средства ограничения дерева достижимости:

1) для нетерминальных и дублирующих вершин не будем строить исходящих из них дуг.

2) будем обозначать неограниченное число фишек в позиции w. причём w±a=w,a=const

3.1.2. Алгоритм построения дерева достижимости.

Алгоритм начинает работу с начальной маркировки и работает до тех пор, пока в дереве есть граничные вершины.

Пусть x - граничная вершина, которую нужно обработать.

1) если в дереве есть другая вершина y: μ[x]= μ[y], то х – дублирующая.

2) если для маркировки μ[x] ни один из переходов не разрешён, т.е. σ(μ[x], t_j) не определено для любого t_j , то х – терминальная вершина.

3) для всякого перехода t_j разрешённого в μ[x] создать новую вершину z , маркировка которой определяется следующим образом:

а) если μ[x]_i=w , то μ[z]_i=w.

б) если на пути от корневой вершины к х, существует вершина y с μ[y] < σ(μ[x], t_j) и μ[y]_i < σ(μ[x]_i, t_j) то μ[z]_i=w.

в) в противном случае μ[z]_i = σ(μ[x]_i, t_j).

Лемма1: В любом ∞ направленном дереве, в котором всякая вершина имеет только конечное число непосредственно последующих вершин, существует ∞ путь, исходящий из корня.

Лемма2: Всякая ∞ последовательность неотрицательных целых, содержит ∞ неубывающую подпоследовательность.

Лемма3: Всякая ∞ последовательность n-векторов над расширенными неотрицательными целыми (неотрицательные целые и w) содержит ∞ неубывающую подпоследовательность.

Теорема: Дерево достижимости сети Петри конечно.

3.1.3. Блок-схема дерева достижимости.

Общий путь построения дерева достижимости заключается в определении всех разрешенных переходов в соответствующей маркировке с последующим анализом соответствующего очередного состояния маркировки, достигающихся при независимых автоматических последовательностей запусков всех разрешенных переходов предыдущей маркировки.

М^I – вершины дерева,

Q^J – очередь разрешенных пеерходов,

t_j – переходы.

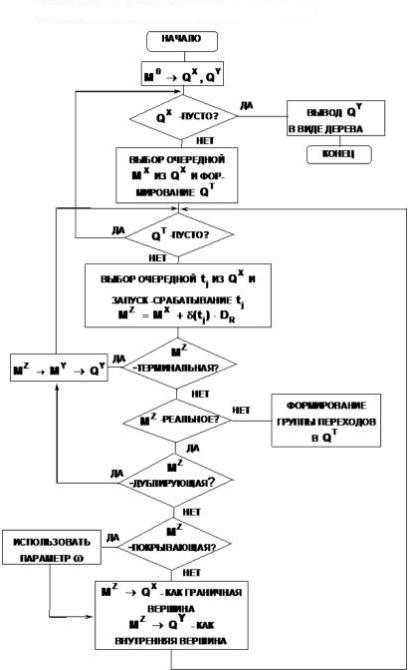
Рис. 3.1.3.1. Блок-схема дерева достижимости.