Решение систем линейных уравнений

Общая характеристика методов решения систем линейных уравнений

Способы решения систем линейных уравнкний в основном разделяются на две групииы:1)точные методы,представляющие собой конечные алгорифмы для вычисления корней системы(таковы,например.правило Крамера,метод Гаусса,метод главных элементов,метод квадратных корней и др.),и 2)итерационные методы,позволяющие получать корни системы с заданной точностью путем сходящихся бесконечных процессов (к числу их относятся метод итерации,метод Зейделя,метод релаксации и др.).

Вследствие неизбежных округлений результаты даже точных методов являются приближенными,причем оценка погрешностей корней и общем случае затруднительна.при использовании итерационных процессов.сверхтого,добавляется погрешность метода.

Заметим,что эффективное применение итерационных методов существенно зависит от удачного выбора начального приближения и быстроты сходимости процесса.

Решение систем с помощью обратной матрицы.

Формулы Крамера

Пусть дана система n линейных уравнений с n неизвестными

(1)

Обозначим через матрицу из коэффициентов системы (1),через

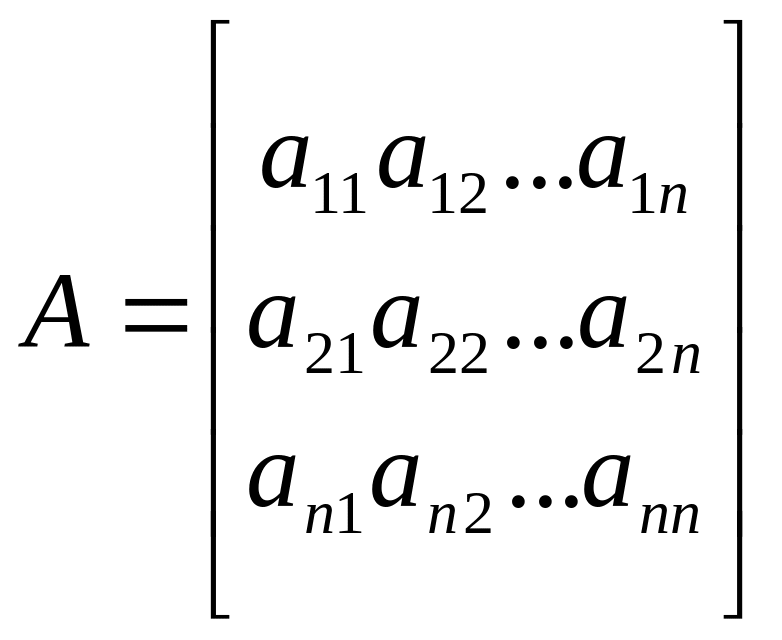(2)

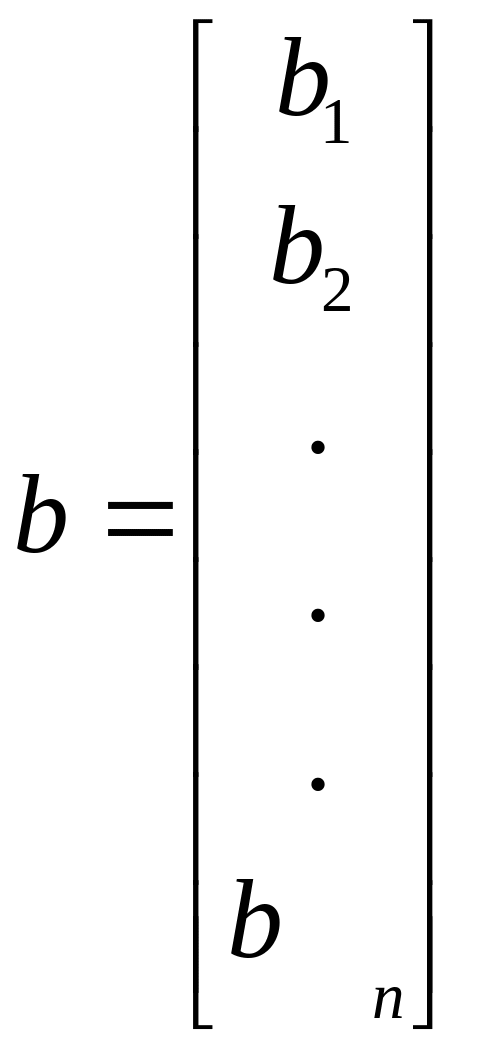
(3)

-столбец ее свободных членов и через

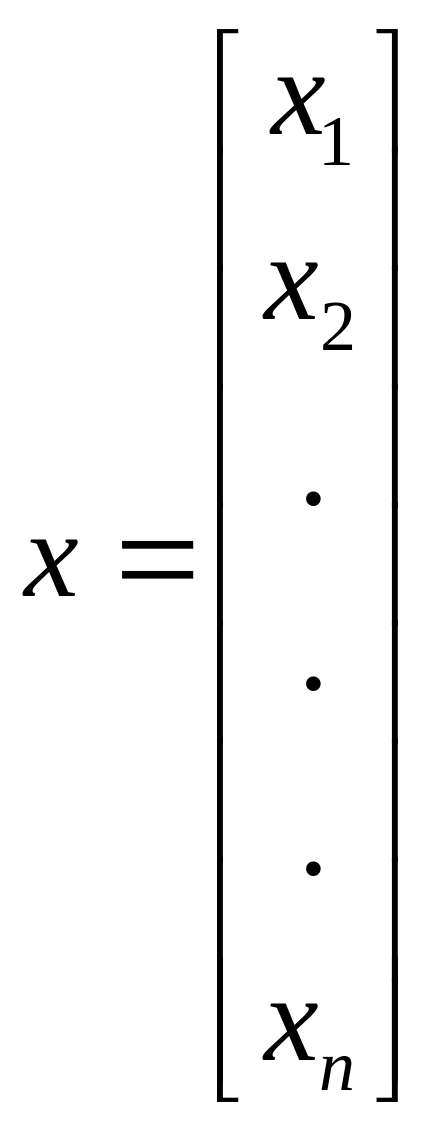
(4) -столбец из неизвестных(искомый вектор).Тогда система(1) кратко может быть записана в виде матричного уравнения

(5)

Совокупность чисел x₁,x₂,….x_n(или короче,вектор ч),обращающих систему (1) в тождество ,называется решением этой системы ,а сами числа х_i ее корнями.

Если матрица А-неособенная.т.е.

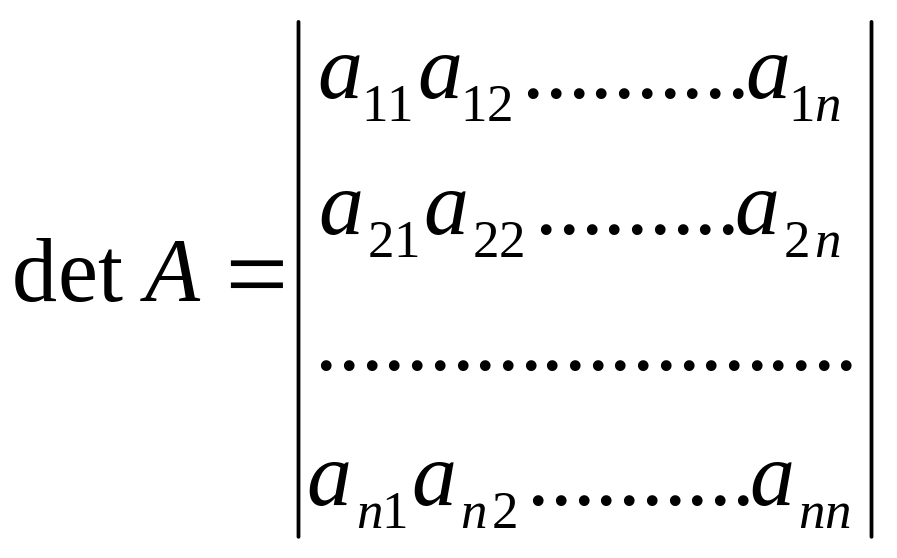= (6)

то система (1),или эквивалентное ей матричное уравнение (5),имеет единственное решение.

В самом деле,при условии существует обратная матрица получим

или

(7)

Формула (7),очевидно ,дает решение уравнения (5),причем так как каждое решение имеет вид (7),то решение единственно.

Пример 1.Решить систему уравнений

Решение.запишем систему в матричной форме

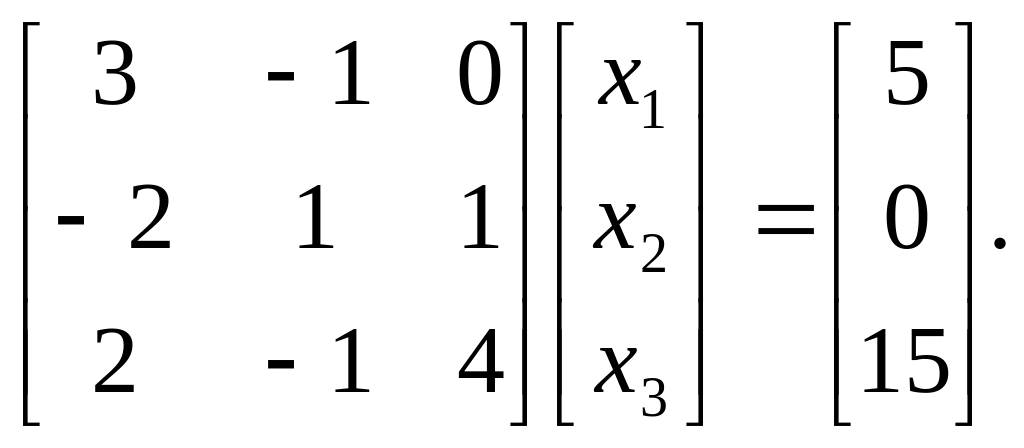
Определить матрицы А данной системы

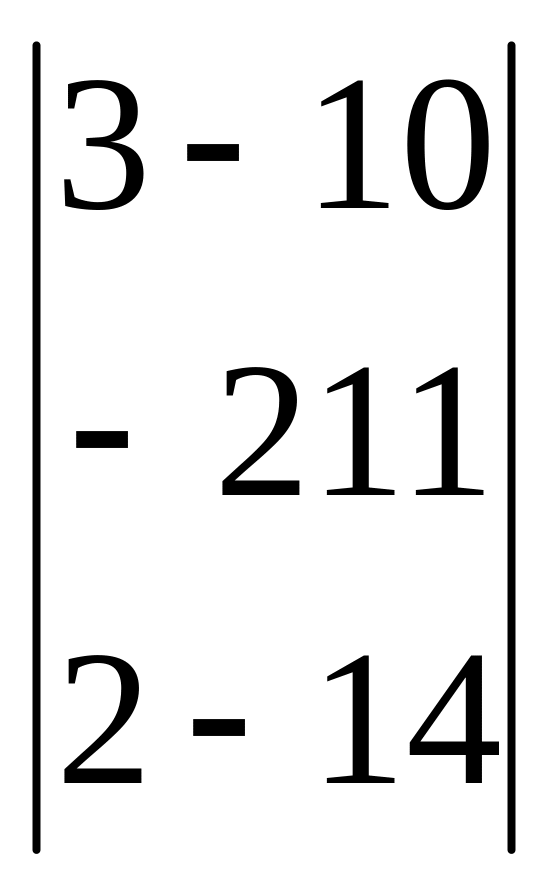=5 .

Вычисляя обратную матрицу А^-1,получим:

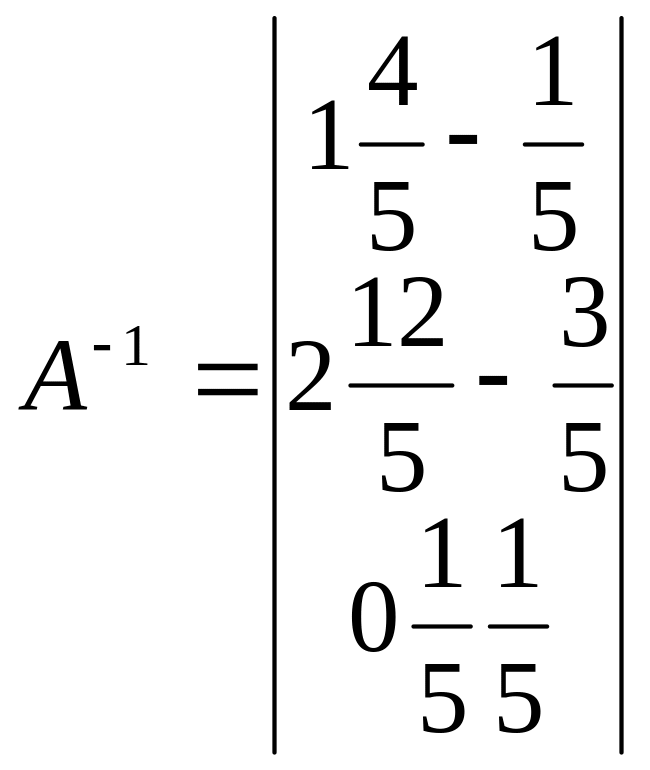
Отсюда

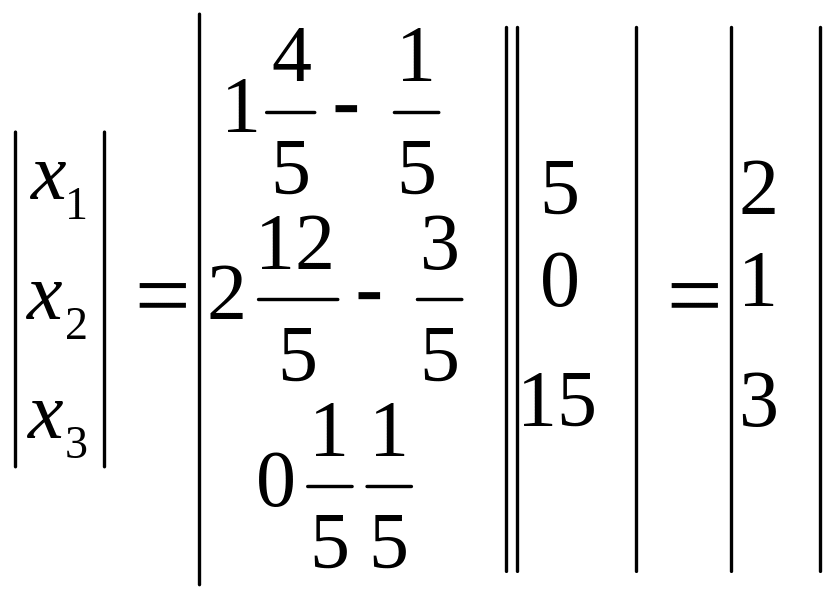
Значит,х₁=2, х₂=2,х=3.

Для матрицы А порядка n>4 непосредственное нахождение обратной матрицы А^-1 требует много времени.Поетому формула(7) редко употребляется на практике.

Пользуясь формулой(7),легко получить формулы для неизвестных системы (1).

где

A=

-матрица,союзная с А (А_ij-алгебраические дополнения элементов a_ij).Поэтому

X=

или

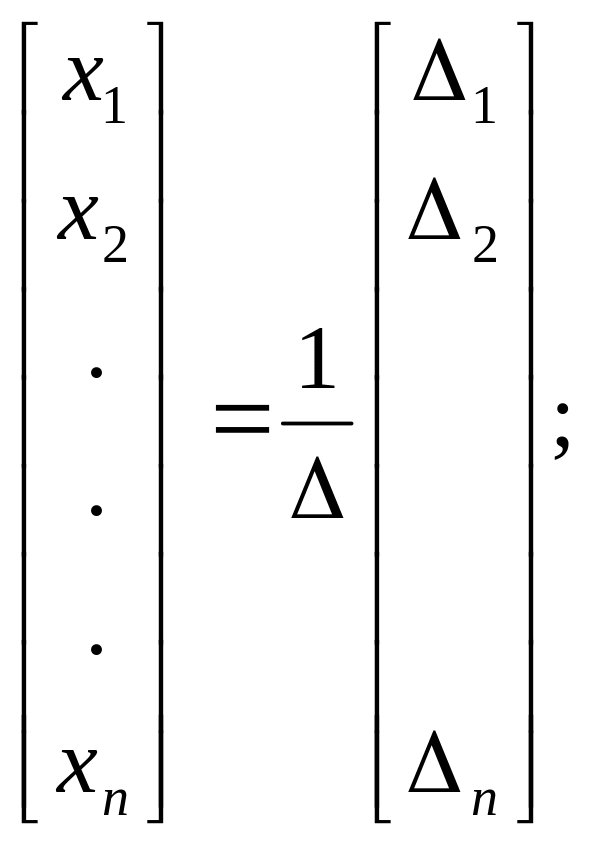
где

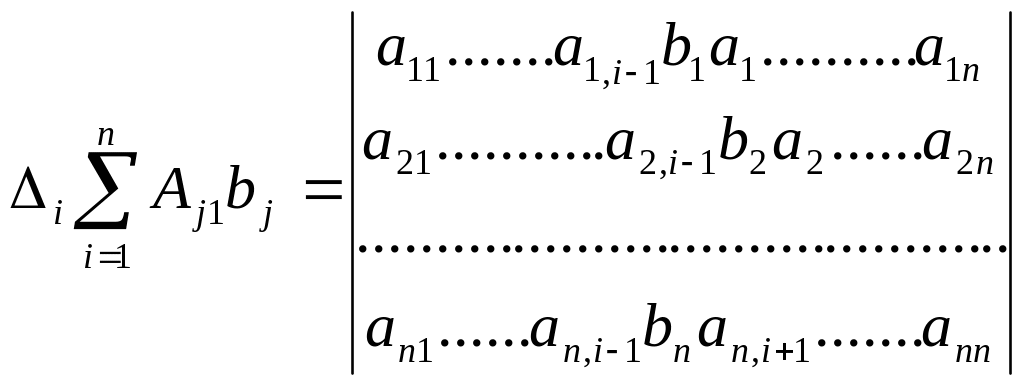
-определители,получающиеся из определителя (формула 6

путем замены его i-го столбца столбцом свободных членов системы (1)

Из равенства (8) получаем формулы Крамера

(9)

Следовательно,если определить системы (1) ,то система имеет единственное решение х,определяемое матричной формулой(7) или эквивалентными ей скалярными формулами (9).

Пример 2.Решить систему линейных уравнений

Решение.определить этой системы

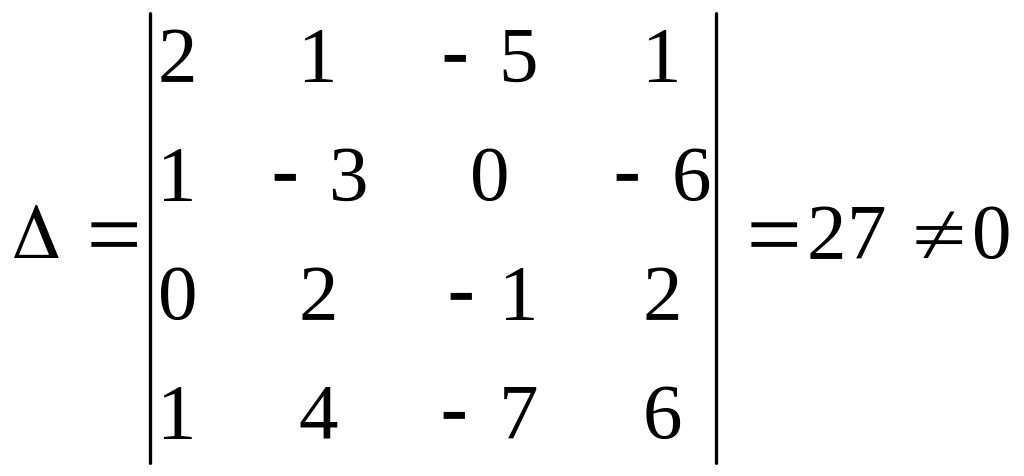
Вычисляя дополнительрые определители,получим:

.

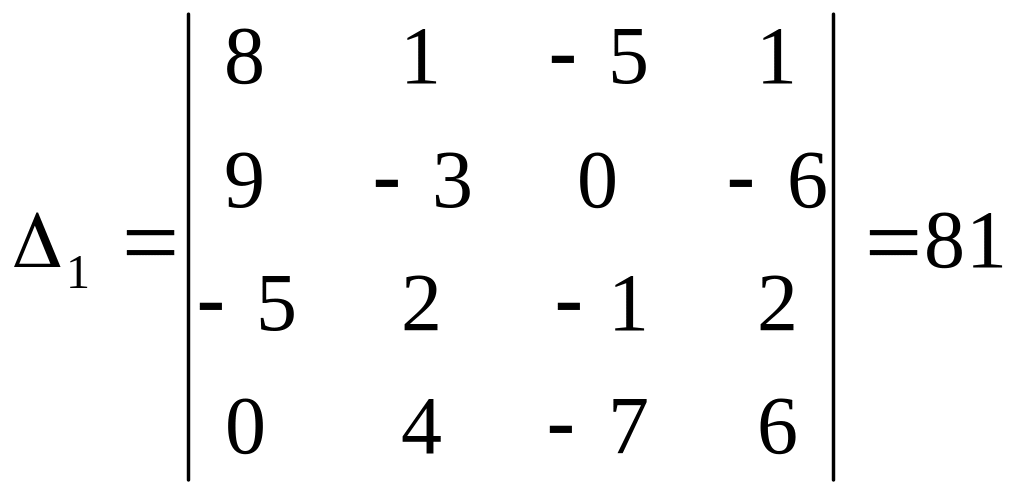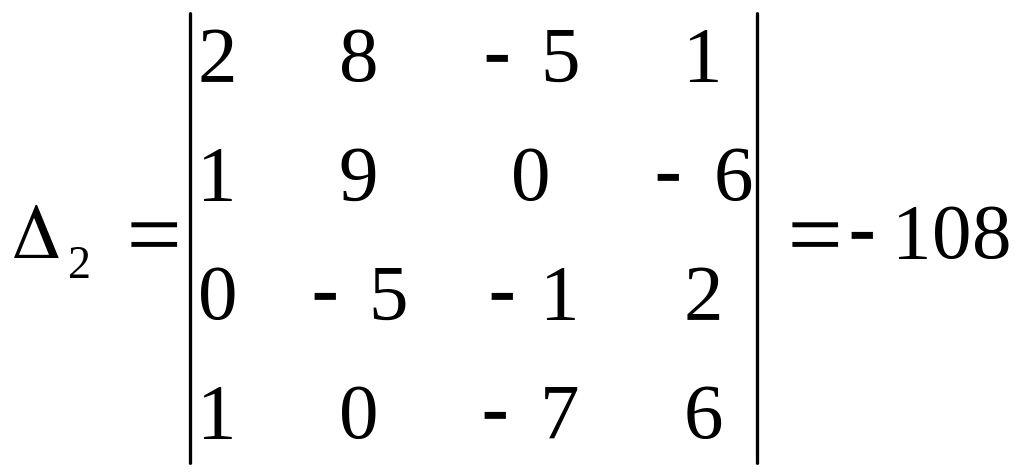
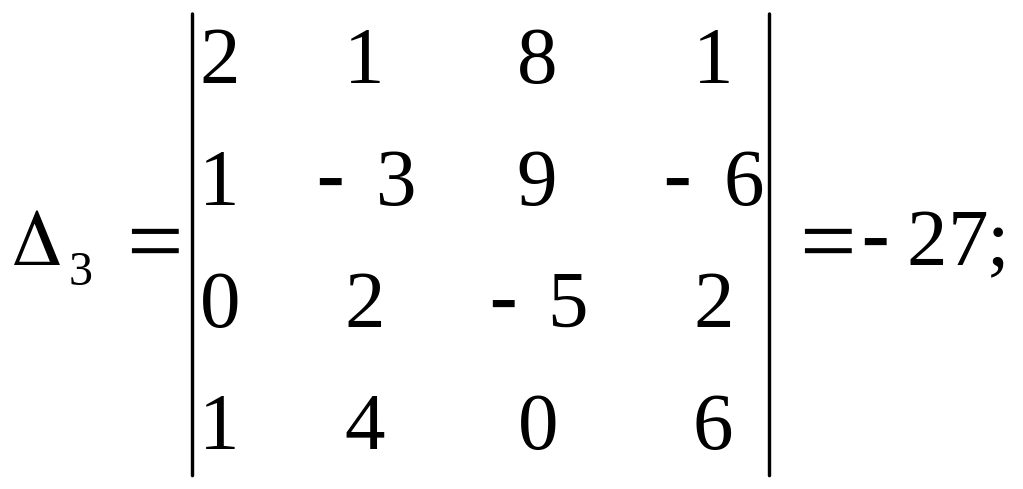
Отсюда

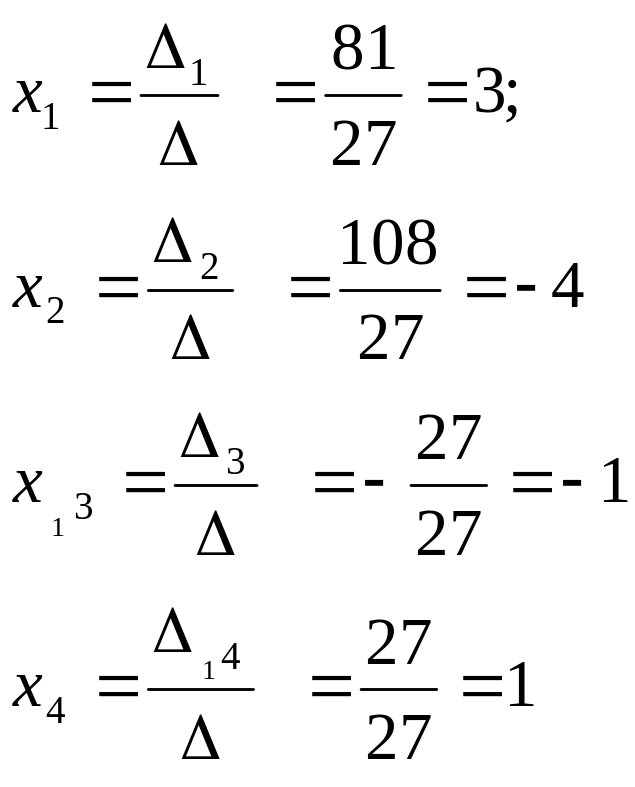
Таким образом ,решение линейной системы (1) с n неизвестными сводится к вычислению (n+1)-го определителя порядка n.Если число n то вычисление определителей является трудоемкой операцией.Поэтому разработаны прямые приемы нахождения корней линейной системы.

Метод Гаусса

Наиболее распространеннымим премом решения систем линейных уравнений является алгорифм последовательного исключения неизвестных.Этот метод носит название метода Гаусса.Для простоты рассуждений ограничемся рассмотрением системы четырех уравнений неизвестными

(1)

Пусть (ведущий єлемент).Разделив коєффициентыпервого уравнения системы(1) на а₁₁,получим :

(2)

где

Метод Гаусса

Пользуясь уравнением (2).легко исключить из системы (1) неизвестную х₁

Для етого достаточно из второго уравнения системы (1) вычесть уравнение(2),умноженное на а₂₁,из третьего уравнения системы (1) вычесть уравнение (2),умноженное на а₃₁,и т.д.

В результате получим систему из трех уравнений

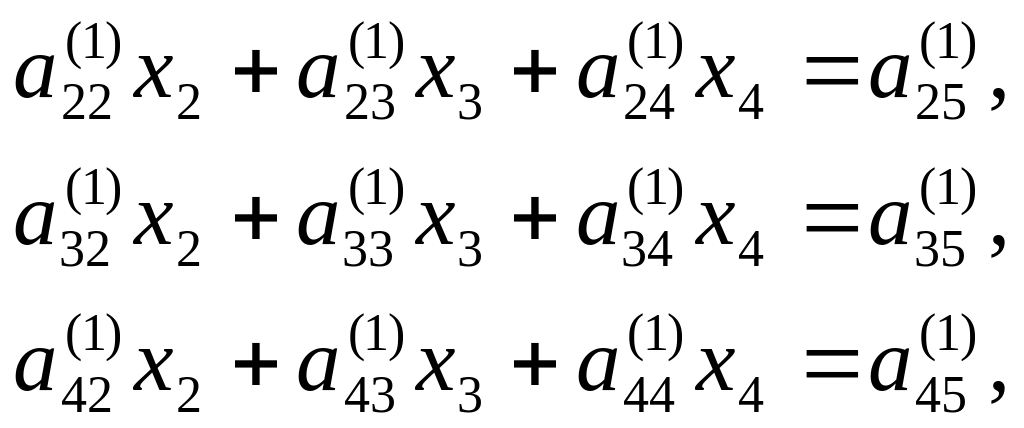
где коэффициенты вычисляются по формуле

=

Разделив ,далее.коэффициенты первого уравнения системы на ведущий элемент ,получим уравнение

где

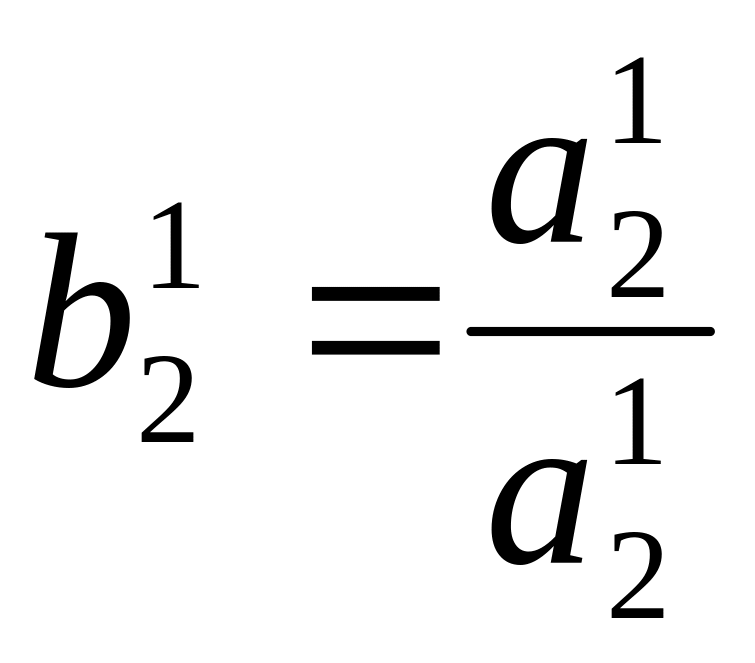
Исключая теперь х₂ таким же способом,каким мы исключили х₁ ,придем к следующей системе уравнений:

Таким образом,процесс решения линейной системы по методу Гаусса сводится к построению эквивалентной системы имеющей треугольную матрицу.необходимым и достаточным условием примеримости метода является неравенство нулю всех ведущих элементов.вычисления удобно поместить в таблицу 13.приведенная в ней схема называется схемой единственного деления.процесс нахождения коэффициентов треугольной системы обычно называется прямым ходом,процесс получения значений неизвестных-обратным ходом.

Прямой ход начинается с выписыванием коэффициентов системы,включая свободные члены(раздел а).последняя строка раздела А схемы представляет собой результат деления первой строки раздела на ведущий элемент а11.Эементы следующего раздела схемы (раздел А1)равны соответствующим элементам предстшествующего раздела безпроизведения их проекций на ряды раздела А,содержащие элемент 1(т.е. на первый столбец и последнюю строку).

Последняя строка раздела А1 находится путем деления первой строки раздела на ведущий елемент.Аналогично строятся следующие разделы.Прямой ход заканчивается,когда мы дойдем до раздела,состоящего из одной строки,не считая преоброзованной.

При обратном ходе используются лишь строки разделов а1,содержащие единицы,начиная с последней.элемент из разделаА3,стоящий в столбце свободных членов отмеченной строки раздела,дает значение Х4.Далее,все остальное неизвестные х(i=3,2,1) шаг за шагом находятся с помощью вычитывания из свободного члена отмеченной строки суммы произведений ее коэффициентов на соответствующие значения ранее нацденных неизвестных.Значения неизвестныхпоследовательно выписывабтся в последний раздел В.расставленные там единицы помогают находить дляч сооттвеиствующие коэффициенты в отмеченных строках.

Схема е6динственного деления

х	х	х	х	Свободные члены		Разделы схемы
						А
						А
						А
						А
1	1	1	1			В

Если a_ib принятьза новые свободные члены в системе(1),то преоброзованная линейная система

(i=1,2,3,4) (4)

будет иметь неизвестные х_j,связанные с прежними неизвестними х_j соотношениями

(J=1,2,3,4). (5)

В самом деле ,подставляя формулы(5) в уравнение(4),в силу системы(1) и формул (3)получим тождество

(J=1,2,3,4).

Вообще ,если над контрольними суммами в каждой строке проделывать те же операции,что и над остальними елементами зтой строки ,то при отсутствии ошибок в вычислении елементи столбца равны суммам элементоа соответствующих преобразованных строк.Это Обстоятельство служит контролем прямого хода.Обратный ход контролируется нахождением чисел х_j ,которие должны совпадать с числами х_j+1

Пример.Решить систему

Решение.В раздел А таблицы 14 впишем матрицу коэффициентов системы,ее свободные члены и контрольные суммыюДалее,заполняем последнюю (пятую ) строку раздела А ,деля первую строку на 7,9 (на а₁₁).

Переходим к заполнению раздела А1 таблицы.Взяв любой элемент раздела А(не находящийся в первой строке),вычитываем из него произведение первого элемента его строки на последний элемент столбца,к которому он принадлежыт,и записываем на сответстаующее место в разделе,и записываем на соответствующее место в разделе А1 схемы.Например ,выбрав а₄₃=-8,9,будем иметь

Чтоби получить последнюю строку раздела А1.делим все члены первой строки этого раздела на Например,

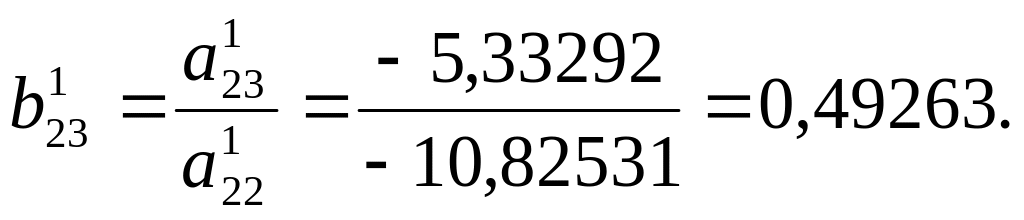
Метод Гаусса

x	x	x	x	Свободные разделы		Разделы схемы
7,9 8,5 4,3 3,2	5,6 -4,8 4,2 -1,4	5,7 0,8 -3,2 -8,9	-7,2 3,5 9,3 3,3	6,68 9,95 8,6 1	18,68 17,95 23.2 -2,8	А
1	0,70886	0,72152	-0,91139	0,84557	2,36456	А
	-10,82531 1,15190 -3,66835	-5,33292 -6,30254 -11,20886	11,24682 13,21898 6,21645	2,76265 4,96405 -1,70582	-2,14876 13.03239 -10,36658	А
	1	0,49263	-1,03894	-0,25520	0,19849
		-6.87000 -9,40172	14,41573 2,40525	5,25801 -2,64198	12,80374 -9,63845	А
		1	-2,09836	-0,76536	-1,86372
			-17,32294	-9.83768	-27,16062	А
			1	0,56790	1,56790
1	1	1	1	0,56790 0,42630 0,12480 0.96710	1,56790 1,42630 1,12480 1,96710	А

Аналогичным путем заполняются остальные разделы таблицы.

Например,

Для нахождения неизвестных используем строки ,содержащие единицы,начиная с последней(отмеченные строки).Неизвестное х4 представляет собой свободный член последней строки раздела А3

Значення остальных неизвестных х3,х2,х1 получаются последовательно в результате вычитания из свободных членов отмеченных в таблице.

Имеем

Текущий контроль вычислений осуществляется с помощью столбца,над которим производится те же децствия ,что и надостальными столбцами.

В результате:1(сумма елементов каждой строки схемы должна быть равна элементуэтой строки из столбца.2)корни х,соответствующих столбцу должны быть на единицу больще соответствующих корней системы.

Кстати.если учесть единицы,написанные в разделеВ,то опять получится,что и в етом разделе элементы столбца являются суммами элементов отвечающих им строк.В нашем случае первое и второе условия выполняются с точностью до единицы последнего разряда.следовательно,почти достоверно,что вычисления выполнены правильно.

Для прямого хода требуется следующее число умножений и делений

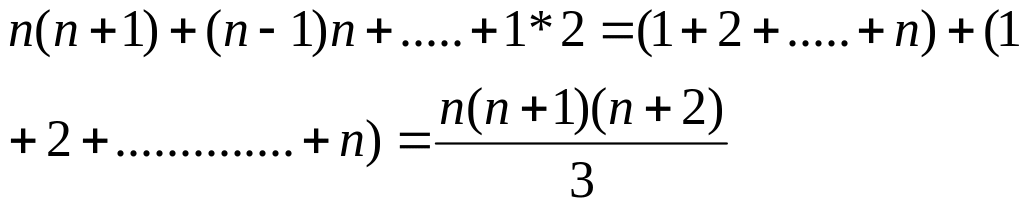
Таким образом,время,необходимое для решения линейной системы методомГаусса,примерно пропорцианально кубу числа реизвестных.Например,для рещения методом гаусса системы 100 линейных уравнений со 100 неизвестными на быстродействующий машине,выполняющей много операций в секунду.

=100 сек