Лекция 5

2. Приближенные методы

2.1 Метод конечных разностей

Очень часто точное решение в силу переменности поперечного сечения получить не представляется возможным. Рассмотрим один из наиболее употребительных приближенных методов – метод конечных разностей.

Область определения задачи разбивается на m равных участков с шагом h [2] (рис. 14), причем .

Рис.14. К понятию о конечных разностях

Первые производные в конечно-разностной форме имеют вид:

(2.1.1)

Вторая производная:

. (2.1.2)

Уравнение упругого равновесия (5) в конечно-разностной форме принимает вид:

. (2.1.3)

Алгоритм решения задачи в конечных разностях:

1. Дифференциальное уравнение в конечных разностях (2.1.3) записывается для всех внутренних точек стержня.

2. Учитываются геометрические и статические граничные условия.

3. Решается система алгебраических уравнений, в результате получается массив узловых перемещений.

4. Осуществляется переход от поля перемещений к усилиям.

Покажем на примерах процесс решения. Дифференциальное уравнение упругого равновесия (5) записывается в конечно-разностной форме

. (2.1.4)

В правой части введено обозначение

. (2.1.5)

Здесь

, (2.1.6)

где m – число участков (в нашем случае m=4), на которые разбивается область решения (длина стержня l). Конечноразностные уравнения (2.1.4) записываются для внутренних точек стержня. Для варианта А такими точками являются точки 2,3,4 (рис. 15).

Рис.15. Узловые точки для варианта граничных условий А

Система уравнений для внутренних точек запишется так:

(2.1.7)

Учет однородных геометрических граничных условий (u₁=u₅=0) приводит к системе трех алгебраических уравнений

(2.1.8)

решение которых удобно получать способом Крамера. Определители третьего порядка удобно получать путем разложения по элементам строки или столбца, имеющих нулевой элемент, как это показано для Δ (остальные определители находятся аналогично, звездочками отмечены элементы, по которым производится разложение).

Находим значения узловых перемещений, раскрывая  и приводя их к размерности точного решения.

(2.1.9)

Следует помнить, что запись дифференциального уравнения в конечноразностной форме означает линейную аппроксимацию поля перемещений между узловыми точками. Переход от перемещений к усилиям осуществляется с помощью конечноразностного соотношения

. (2.1.10)

Так как функция перемещений в этом случае кусочно – линейная, то усилие, выражающееся через первую производную от перемещения, будет изображаться кусочно – постоянной функцией.

(2.1.11)

Результаты расчета представлены в таблице 4 (в скобках указаны значения точного решения) и на графиках (рис. 16, 17)

Таблица 4

	0	0.25	0.5	0.75	1.0
	0 (0)	0.797 (0.797)	1.125 (1.125)	0.89 (0.891)	0 (0)
	3.188 (4)	1.312 (2.313)	-0.94 (0.25)	-3.56 (-2.188)	- (-5)

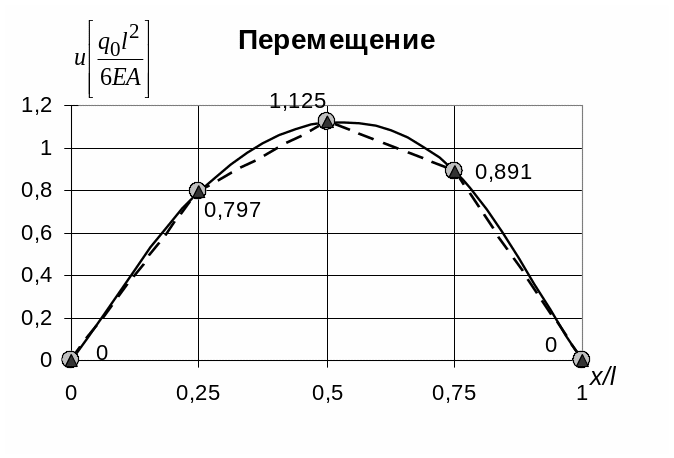
Рисунок 16. Изменение перемещения по длине стержня (решение МКР – вариант А)

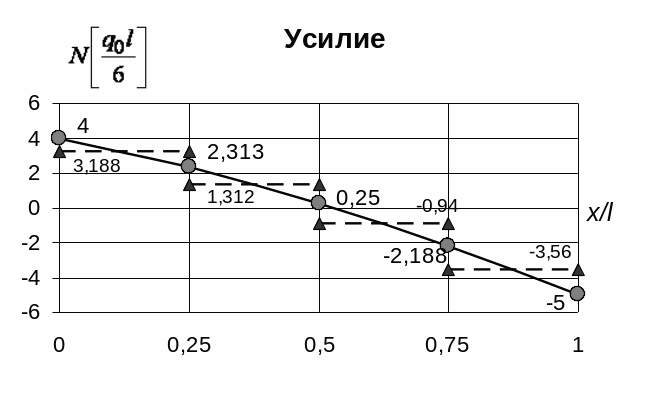
Рис. 17. Изменение продольного усилия по длине стержня (решение МКР – вариант А)

Узловые значения перемещений совпадают со значениями, полученными в точном решении. Значения продольной силы значительно отличаются и по значениям, и по виду графика. Это объясняется тем, что принятые выражения для производных подразумевают линейную аппроксимацию поля перемещений в пределах шага разбиения, т. е. производные в этом случае постоянны. Очевидно, что при увеличении числа точек результаты будут ближе к точным.