Задачи на деревьях
Ациклическим называется граф, в котором отсутствуют циклы.
Граф без циклов называется лесом.
Дерево – это связный ациклический граф.
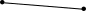
Лес Дерево
Компоненты связности леса – деревья.
Свойства деревьев.
Граф G – дерево, если он связный и число ребер на единицу мкньше числа вершин.
Если G – дерево, тогда любая цепь будет простой.
Любые две вершины дерева можно соединить цепью, притом простой.
Пусть G – дерево. Если добавить одно ребро, то получим ровно один простой цикл.
Понятие дерева имеет в теории нрафов важное значение, так это простой тип графов, и поэтому часто сначала на нем изучаются теоретические вопросы, поставленные для конечных графов. С другой стороны понятие дерева используется для решения различных технических задач. Т.е. имеет прикладное значение.
Рассмотрм одну из таких задач. Для этого введем еще одно определение.
Остовом (покрывающим деревом) графа называется его подграф, являющийся деревом и содержащий все вершины графа.
Пусть требуется n городов соединить сетью дорог. Стоимость строительства каждой дороги между двумя городами известна. Построим граф, в котором вершшины – города, ребра – дороги. Каждому ребру припишем вес, равный стоимости строительства дороги.. определим вес остова, как сумму весов составляющих его ребер.
Проектирование сети дорог сводится к построению остова гарфа, имеющего минимальный вес. В силу связности дерева выполнится условие соединить каждый город с каждой дорогой.
Рассмотрим сначала задачу построения остова без учета весов его ребер. Идея алгоритма состоит в том, что просматриваются в произвольном порядке ребра графа и св соответствии с правилом принимается решение о включении очередного ребра в остов.
Данное правило состоит в проверке условия, при выполнении которого рассматриваемое ребро образует цикл с построенным подграфом. Если условие выполняется, то ребро не включают в остов и окрашивают в красный цвет, если не выполняется, то включают в остов и окрашивают в зеленый цвет.
Работа алгоритма заканчивается после того, как ациклический подграф окажется связным и будет содержать все вершины графа.
Алгоритм построения остова
Шаг 1. Выбрать любое ребро и окрасить в зеленый цвет. Образовать подграф G1 из этого ребра. Выполнить шаг 2.
Шаг 2. Пусть просмотрено i > 1 ребра графа G. Выбрать любое неокрашенное ребро. Возможны четыре варианта.
Вариант а. Окрасить ребро в зеленый цвет и сформировать подграф Gi+1 , добавив к компонентам подграфа Gi новую компоненту связности – рассматриваемое ребро. Выполнить шаг 2.
Вариант б. Окрасить ребро в зеленый цвет и сформировать подграф Gi+1 , объединив две компоненты связности в одну. Выполнить шаг 2.
Вариант в. Окрасить ребро в зеленый цвет и сформировать подграф Gi+1 , добавив к одной компоненте подграфа Gi рассматриваемое ребро. Выполнить шаг 2.
Вариант г. Окрасить ребро в красный цвет, если оно образут в построенным подграфе цикл.
Замечание. Данный алгоритм называется «жадным», т.к. каждое ребро просматривается не более одного раза, т.е. после просмотра оно окрашивается в зеленый или красный цвет , и в рассмотрение больше не включается.
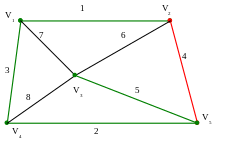
Построим остов для графа, заданного диаграммой, не учитывая вес ребер.
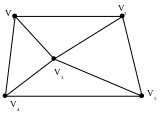
Окрасим ребро {v1, v2} в зеленый цвет.
Окрасим ребро {v4, v5} в зеленый цвет, т.к имеет место вариант а.
Окрасим ребро {v4, v1} в зеленый цвет, т.к имеет место вариант б.
Окрасим ребро {v2, v5} в красный цвет, т.к имеет место вариант г.
Окрасим ребро {v4, v3} в зеленый цвет, т.к имеет место вариант в.
Ациклический подграф содержит все вершины графа, значит остов построен:
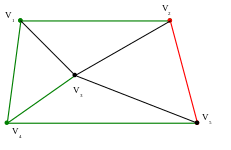
Присвоим каждому ребру вес. И построим остов с минимальным весом (минимальный остов).
Алгоритм построения такого остова отличаеися от вышеизложенного лишь тем, что ребра просматриваются в порядке возрастания их весов. Если на каком – то шаге среди непросмотренных ребер имеется более одного ребра с наименьшим весом, то рассматривается на данном шаге любое из них.
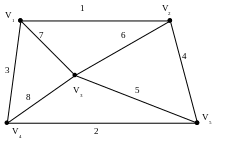
У порядочим ребра графа, переписывая их в порядке возрастания их весов: {v1, v2}, {v4, v5},{v1, v4},{v5, v2},{v3, v5},{v3, v2},{v1, v3},{v4, v3}.
Окрасим ребро {v1, v2}в зеленый цвет.
Окрасим ребро {v4, v5} в зеленый цвет (вариант а).
Окрасим ребро {v1, v4} в зеленый цвет (вариант б).
Окрасим ребро {v5, v2} в красный цвет (вариант г).
Окрасим ребро {v3, v5} в зеленый цвет (вариант в).
Ациклический подграф содержит все вершины графа, значит остов построен:
