4. Обобщение метода математической индукции

Бывают случаи, когда утверждение, неверное для n =1, 2, ... , р - 1, справедливо для n = р. Если затем из предположения о его истинности для n = k>p можно доказать, что оно истинно и для n = k +1, то получаем, что данное выражение истинно для всех n  р.

Пример 6. Докажем, что выражение (кратно 19) для всех натуральных чисел n  3.

Решение. При n = 3 получаем

7³ + 8^23-3 = 343 + 512 = 855 = 45 19

т. е. при n = 3 утверждение верно.

Предположим, что 7^k +8^2k-3 кратно 19 при k >3, и докажем, что 7^k+1 + 8^2(k+1)-3 кратно 19.

По предположению 7^k +8^2k-3 = 19m , где mN , значит,

8^2k-3 = 19m – 7^k.

Отсюда имеем:

7^k+1 + 8^2(k+1)-3 = 7^k+1 + 8^2k-3+2 = 7^k+1 + 648^2k-3 = 7^k+1 + 64(19m – 7^k) = 7^k(7 – 64) + 64 19m = 64  19m – 57  7^k = 19(64m - 37^k),

т. е. выражение кратно 19.

Итак, мы доказали, что утверждение верно для n = 3, и из предположения, что оно верно для n = k>3, доказали его спра­ведливость для n = k + 1. Тогда на основании сказанного выше заключаем, что выражение для всех n  3.

Пример 7. Доказать, что 2ⁿ  5n – 3 при n  5.

При n = 5: 2⁵ = 32, 55 – 3 = 22 и 32 > 22.

Пусть неравенство верно при n = k, k > 5, т.е. 2^k  5k – 3.

Докажем справедливость неравенства при n = k +1, т.е. справедливость неравенства 2^k+1  5(k+1) – 3 или 2^k+1  5k +2.

Умножим обе части неравенства на 2: 2^k+1  2(5k – 3).

Преобразуем правую часть неравенства: 2(5k – 3) = 10k – 6 = 5k + 2 + 5k – 8. Заметим, что 5k – 8  0 при k > 5, тогда 5k + 2 + 5k – 8 > 5k + 2 и, тогда 2^k+1  5k +2.

Контрольные вопросы

1. Сформулировать принцип метода математической индукции.

2. Сформулировать обобщенный метод математической индукции.

3. Вычислить сумму : 2+ 4+ 6+…+2n.

4. Вычислить сумму : 1+3+5+…+(2n-1).

5. Доказать справедливость равенства: 1²+3²+5²+…+(2n-1)² =

6. Доказать справедливость неравенства: 2ⁿ

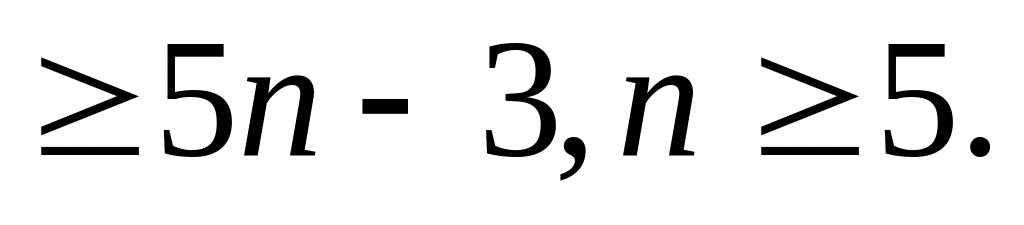
7. Докажите, что истинно высказывание: 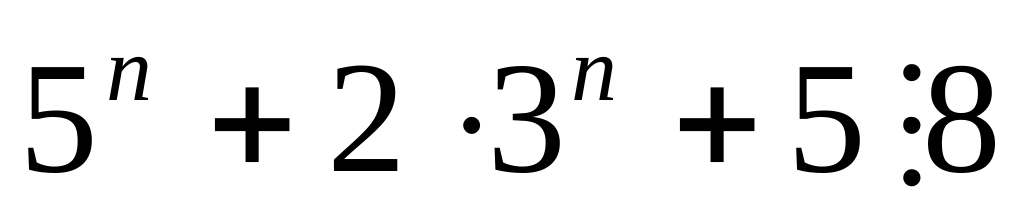при любых натуральных n.

8. Доказать справедливость неравенства:

Лекция 15

ТЕМА: БИНАРНЫЕ ОТНОШЕНИЯ.

ПЛАН:

1. Понятие отношения. Бинарное отношение

2. Операции над бинарными отношениями

3. Свойства бинарных отношений

4. Специальные бинарные отношения

Главная

1. Понятие отношения. Бинарное отношение.

Пусть заданы множества Х₁, Х₂,…,Х_n и рассматривается некоторое подмножество их прямого произведения  Х₁Х₂…Х_n , т.е. множество упорядоченных наборов (а₁, а₂,…,а_n), где а₁Х₁ , а₂Х₂,…,а_nХ_n. Это множество называется n – местным отношением или n –арным предикатом, заданном на множестве Х₁Х₂…Х_n .Если Х₁= Х₂=…=Х_n=М, то  Мⁿ и называется n – местным отношением на множестве М.

Пример: на множестве R³ задан трехместный предикат или трехместное отношение P(x, y, z): «x²+y²+z²=25».

Говорят что а₁, а₂,…,а_n находятся в отношении , если (а₁, а₂,…,а_n) .

Наиболее хорошо изучены двухместные отношения, которые называются бинарными. Приведем определение бинарных отношений, опираясь на определение n – местного отношения.

Пусть даны непустые множества Х и У, и подмножество их прямого произведения  ХУ.  называется бинарным отношением.

Т.е.  - множество упорядоченных пар (х, у). Говорят, что х и у находятся в отношении , если (х, у)  . Допускается запись: х  у , означающая, что (х, у)  .

Элементы х и у называются координатами или компонентами отношения .

Область определения бинарного отношения  называется множество D = {x| существует такое у, что х  у}.

Областью значений бинарного отношения  называется множество R = {y| существует такое х, что х  у}.

Понятие отношения следует рассматривать, как естественное обобщение знакомых нам отношений из математики и из жизненных представлений.

Рассмотрим некоторые примеры бинарных отношений.

1. Отношения на множестве натуральных чисел N:

а) «х  у», например, пары (7,7) и (6,8) принадлежат этому отношению, а пара (8,6) – не принадлежит. Область определения D =N, область значений R=N;

б) «иметь общий делитель, не равный единице». Пары (6,9), (4,2), (4,4) принадлежат этому отношению, а пары (7,9), (5,8) – не принадлежат. Область определения D =N, область значений R=N.

2. Отношение равенства на множестве действительных чисел R: «х = у». Этому отношению принадлежат все пары , в которых координаты равны, например, (9,9), (2,3; 2,3). Область определения D =R, область значений R=R.

3. Отношения на множестве точек декартовой плоскости:

а) «находится на одинаковом расстоянии от начала координат» - это множество всех пар (х,у), где хR и уR, таких, что х² + у² = r², т.е. все точки окружности с центром в начале координат и радиусом r;

б) «быть симметричными относительно оси х» - этому отношению принадлежат пары точек (х,у) и (х,-у).

4. Отношения на множестве людей:

а) «жить в одном городе»;

б) «быть старше (моложе);

в) «быть сыном»;

г) «быть знакомыми».