Лабораторная работа №6 Изучение алгоритмов численного нахождения минимума функций нескольких переменных

Трудности задачи поиска экстремумов, характерные для функции нескольких переменных, проявляются уже при решении задачи поиска минимума функции двух переменных F(x,y). Графически функцию F(x,y) можно изобразить не только в виде плоской поверхности в трехмерном пространстве, но и в виде «плоских» линий уровня , являющихся проекциями на плоскость OXY сечения поверхности z = F(x,y) плоскостью z₀ = F₀.

Выделяют три основных типа рельефа поверхности:

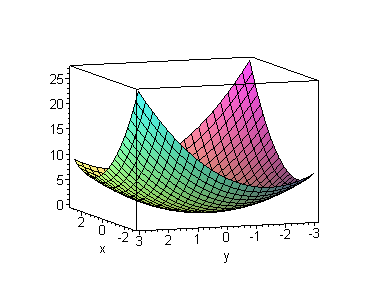
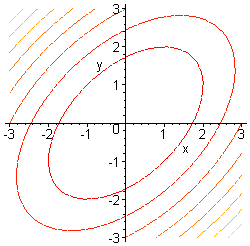
1. Котловинный – линии уровня похожи на концентрические эллипсы (рис. 6.1).

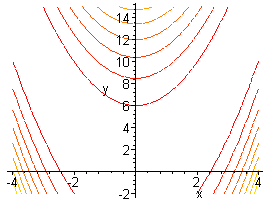
2. Овражный – линии уровня кусочно-гладкие. Геометрическое место точек излома по всем линиям уровня называют истинным оврагом, если угол излома направлен в сторону возрастания функции, или истинным гребнем, если угол излома направлен в сторону убывания функции. К этому же типу относят функции, линии уровня которых имеют не изломы, а участки с очень большой кривизной, называемых разрешимыми оврагами. Например, функция Розенброка - одна из стандартных тестовых функций многомерной оптимизации (рис 6.2).

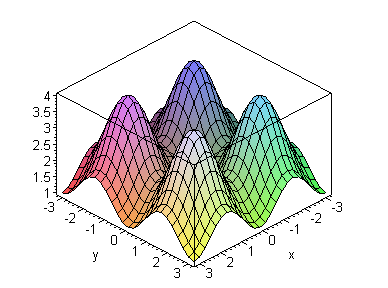
3. Неупорядоченный тип рельефа – характеризуется наличием многих максимумов и минимумов (рис. 6.6).

а b

Рис. 6.1. Поверхность (а) и линии уровня (b)

функции с котловинным рельефом

а b

Рис. 6.2. Поверхность (а) и линии уровня (b) функции Розенброка

с овражным рельефом

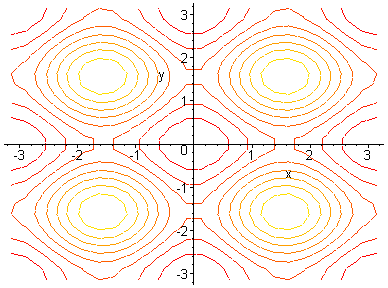
а b

Рис. 6.6. Поверхность (а) и линии уровня (b) функции

с неупорядоченным рельефом

Рассмотрим несколько методов поиска минимума функции нескольких переменных.

Изучение алгоритмов численного нахождения минимума функции нескольких переменных в Excel

Найдем минимум функции F(x,y)=sin(y)*cos(x) в области x[‑3,3], y[-3,0]. Чтобы представить себе тип исследуемой поверхности, постройте в программе MathCAD её график.

Метод покоординатного спуска.

Задание 1: Начинать можно с любой точки (x₀,y₀), принадлежащей указанной области.

1 шаг: фиксируем одну координату (присваиваем ей некоторое конкретное значение), например, координату x. Находим экстремум получившейся функции одной переменной y либо аналитически, либо любым из изученных численных методов. В результате получили некоторое промежуточное значение y_min1.

2 шаг: фиксируем другую координату y = y_min1. Находим экстремум получившейся функции одной переменной x. В результате получили некоторое промежуточное значение x_min1.

3 шаг: снова фиксируем первую координату x = x_min1. Находим экстремум получившейся функции одной переменной y любым из изученных методов. В результате получили некоторое промежуточное значение y_min2.

4 шаг: получаем значение x_min2.

И т.д.

Расчет заканчиваем в том случае, когда расстояние d от предыдущей точки (x_mini-1, y_mini-1) до точки, полученной в результате последней итерации (x_mini, y_mini), станет меньше выбранной вами точности. Результаты промежуточных вычислений оформите в виде таблицы.

Метод Хука-Дживса.

Задание 2: Исследующий поиск начинать можно с любой точки (x₀,y₀), принадлежащей указанной области. Далее нужно выбрать величину шага, которая может быть различной для разных координатных направлений. Для удобства выберите одинаковый шаг h=0,1.

1 шаг: считаем значение функции в базовой точке F₀=F(x₀,y₀). Делаем шаг вправо и считаем значение функции в найденной точке F₀₁=F(x₀+h,y₀). Если F₀₁<F₀, то мы сделали шаг в нужном направлении, в обратном случае делаем шаг влево и считаем значение функции в другой точке F₀₂=F(x₀-h,y₀). Если F₀₂<F₀, значит, мы сделали шаг в нужном направлении, в обратном случае координата x на этом шаге не изменяется.

Теперь делаем шаг вверх и считаем значение функции в найденной точке F₀₃=F(x₀,y₀+h). Если F₀₃<F₀, то мы сделали шаг в нужном направлении, в обратном случае делаем шаг влево и считаем значение функции в другой точке F₀₄=F(x₀,y₀-h). Если F₀₄<F₀, значит, мы сделали шаг в нужном направлении, в обратном случае нужно уменьшить значение шага (например, вдвое), так как мы подошли слишком близко к точке минимума.

В результате вышеописанных действий мы получили новое значение базовой точки (x₁,y₁).

2 шаг: Считаем значение функции в базовой точке F₁=F(x₁,y₁). Попытаемся выполнить поиск по образцу. Делаем такие же шаги в направлении обеих осей, которые привели к успеху на шаге 1. Получаем точку (x₂,y₂), считаем значение F₂=F(x₂,y₂). Если F₂<F₁, поиск по образцу завершился успехом, и шаг 2 можно повторить. В противном случае возвращаемся к шагу 1 с базовой точкой (x₁,y₁).

Результаты промежуточных вычислений можно оформить в виде таблицы со следующими заголовками:

H	x	y	x+h	x-h	y+h	y-h	f(x,y)	f(x+h,y)	f(x-h,y)	f(x,y+h)	f(x,y-h)
[…]	[…]	[…]	[…]	[…]	[…]	[…]	[…]	[…]	[…]	[…]	[…]

Расчет заканчиваем, когда значение шага будет меньше выбранной вами точности (не более 0,01).

Метод градиентного спуска.

Задание 3: Будем двигаться к минимуму в направлении наиболее быстрого убывания функции (в антиградиентном направлении). Выберите некоторое начальное приближение (x₀,y₀) и найдите в данной точке значения градиента h_x=F/x при x = x₀ и h_y=F/y при y = y₀. Теперь нам нужно сделать шаг в антиградиентном направлении: x_i = x_i-1 - α·h_x, y_i = y_i-1 - α·h_y. Расчет заканчиваем в том случае, когда расстояние d от предыдущей точки (x_i-1, y_i-1) до точки, полученной в результате последней итерации (x_i, y_i), станет меньше выбранной вами точности. Результаты промежуточных вычислений оформите в виде таблицы:

α	x	y	d/dx	d/dy	f(x,y)	d
[…]	[…]	[…]	[…]	[…]	[…]	[…]