- •Раздел 1. Основные понятия и определения та у 7
- •Раздел 2. Получение информации для анализа и синтеза аср. Принципы построения математических моделей элементов аср 29
- •Раздел 3. Динамические характеристики линейных систем 50
- •Раздел 4. Типовые динамические звенья. Переходные и частотные характеристики типовых звеньев 69
- •Раздел 5. Характеристики замкнутых аср 88
- •Раздел 6. Анализ устойчивости линейных систем 106
- •Раздел 7. Качество процессов управления 140
- •Раздел 8. Косвенные критерии качества 154
- •Раздел 9. Параметрический синтез типовых регуляторов 169
- •Раздел 10. Нелинейные системы. Общая характеристика нелинейных аср 173
- •Раздел 11. Системы регулирования при случайных воздействиях 214
- •Раздел 12. Дискретные (цифровые) автоматические системы регулирования (цаср) 245
- •Раздел 13. Анализ устойчивости дискретных систем 274
- •Раздел 14. Адаптивные системы 293
- •Раздел 1. Основные понятия и определения та у
- •1.1 Цель и задачи дисциплины. Кибернетика. Основные понятия тау. Принципы автоматического регулирования Цель и задачи дисциплины
- •Кибернетика
- •Основные понятия тау
- •Объект автоматического управления
- •Примеры объектов и систем управления
- •Примеры систем управления
- •Функциональные и структурные формы объектов
- •Принципы автоматического регулирования (управления)
- •Пример простейшей непрерывной замкнутой системы регулирования и ее функциональная схема
- •1.2 Классификация аср. Задачи курса тау Классификация аср
- •Задачи курса тау
- •Раздел 2. Получение информации для анализа и синтеза аср. Принципы построения математических моделей элементов аср
- •2.1 Принципы построения математических моделей элементов аср. Линеаризация. Примеры моделей звеньев Принципы построения математических моделей элементов аср
- •Дифференциальные уравнения
- •Составление математической модели
- •Линеаризация
- •Передаточные функции сау. Преобразования Лапласа
- •Примеры моделей звеньев
- •Раздел 3. Динамические характеристики линейных систем
- •3.1 Динамические характеристики линейных систем. Типовые входные воздействия, их спектры и изображения. Временные характеристики - импульсная (весовая) и переходная. Свойства. Уравнения свертки
- •3.2 Частотные характеристики, логарифимические частотные характеристики. Связь с передаточной функцией. Свойства и расчет частотных характеристик по передаточной функции
- •Ориентированные графы систем автоматического управления
- •Использование формулы Мейсона для преобразования структурных схем и ориентированных графов
- •Раздел 4. Типовые динамические звенья. Переходные и частотные характеристики типовых звеньев
- •Минимально фазовые и неминимально фазовые звенья
- •Типовые звенья. Характеристики звеньев
- •Раздел 5. Характеристики замкнутых аср
- •Замкнутые системы автоматического управления. Виды обратной связи
- •Передаточные функции в системах автоматического управления
- •Комбинированные аср
- •Каскадные аср
- •Расчёт настроек регуляторов в каскадных аср
- •Последовательность расчёта настроек регуляторов
- •Раздел 6. Анализ устойчивости линейных систем
- •6.1 Понятия о критериях устойчивости. Теоремы ляпунова об оценке устойчивости по линеаризованным моделям. Критерии устойчивости рауса и гурвица Понятия о критериях устойчивости
- •Критерии устойчивости
- •Теоремы Ляпунова об оценке устойчивости по линеаризованным моделям
- •Алгебраические критерии устойчивости
- •Критерий устойчивости Гурвица
- •Критерий устойчивости Рауса
- •6.2 Критерии михайлова и найквиста. Анализ устойчивости систем с запаздыванием. Логарифмический критерий устойчивости Частотные критерии устойчивости Принцип аргумента
- •Критерий устойчивости Михайлова
- •Критерий устойчивости Найквиста
- •Устойчивость систем с запаздыванием
- •Об исследовании точности систем с запаздыванием
- •Логарифмический критерий устойчивости
- •Логарифмическая форма критерия Найквиста
- •Структурно-неустойчивые (устойчивые) системы автоматического регулирования
- •Раздел 7. Качество процессов управления
- •Методы построения переходных процессов
- •Метод Акульшина
- •Метод трапеций Солодовникова
- •Точность в установившихся режимах
- •Введение астатизма
- •Метод коэффициентов ошибок
- •Раздел 8. Косвенные критерии качества
- •8.1 Косвенные критерии качества. Корневые критерии качества — степень устойчивости и степень колебательности
- •Степень устойчивости
- •Степень колебательности
- •Частотные критерии качества
- •Запас устойчивости
- •Оценка быстродействия сар
- •Интегральные оценки качества
- •Аналитический расчет квадратичных ит-оценок
- •Раздел 9. Параметрический синтез типовых регуляторов
- •9.1 Параметрический синтез типовых регуляторов Постановка задачи синтеза. Основные методики расчета настроек регуляторов. Условия компенсации низкочастотных возмущений
- •9.2 Расчет настроек на заданную степень колебательности, Расчет настроек на заданный показатель колебательности м и me
- •9.3 Приближенные методики расчета настроек. Расчет настроек в комбинированных и каскадных аср. Робастные методы расчета настроек
- •Формульный метод определения настроек регулятора
- •Раздел 10. Нелинейные системы. Общая характеристика нелинейных аср
- •10.1 Нелинейные системы. Общая характеристика нелинейных аср. Типовые нелинейные модели. Уравнения нелинейных систем
- •Характеристика нелинейных систем
- •Особенности нелинейных систем
- •Типовые нелинейные элементы системы управления
- •10.2 Анализ нелинейных систем на фазовой плоскости. Классификация особых точек. Автоколебания. Метод точечных преобразований
- •Основные понятия
- •Фазовые портреты нелинейных систем
- •Методы построения фазовых портретов
- •Интегрирование уравнений фазовых траекторий
- •Метод изоклин
- •Метод припасовывания
- •Метод сшивания
- •Понятие об автоколебаниях
- •Методы исследования автоколебаний Критерий Бендиксона
- •Метод точечного преобразования y1
- •10.3 Анализ релейных систем. Понятие устойчивости по ляпунову. Устойчивость в малом, большом и целом Устойчивость в малом, большом и целом
- •Исследование устойчивости нелинейных систем. Второй метод Ляпунова
- •10.4 Абсолютная устойчивость положения равновесия. Критерий в.М. Попова Критерий в.М. Попова
- •Процедура проверки абсолютной устойчивости
- •Метод гармонической линеаризации
- •Основное уравнение метода гармонического баланса
- •Способ Гольдфарба
- •Коррекция автоколебаний
- •Условия применимости метода гармонического баланса
- •Вибрационная линеаризация
- •Раздел 11. Системы регулирования при случайных воздействиях
- •11.1 Случайные процессы в аср. Типовые случайные сигналы и их характеристики Случайные процессы в аср
- •Характеристики случайных сигналов
- •11.2 Преобразование случайных сигналов линейным звеном. Идентификация динамических характеристик при случайных процессах Преобразование случайного сигнала линейным динамическим звеном
- •Определение оптимальной передаточной функции системы управления
- •11.3 Задачи анализа и синтеза аср при случайных воздействиях. Расчет дисперсии ошибки, параметрический синтез аср по минимуму дисперсии Задачи анализа и синтеза аср при случайных воздействиях
- •Расчет ошибок с сау при случайных воздействиях
- •Вычисление и минимизация дисперсии сигнала ошибки замкнутой системы
- •Статистическая оптимизация систем управления
- •Раздел 12. Дискретные (цифровые) автоматические системы регулирования (цаср)
- •Импульсный элемент
- •Линейные разностные уравнения
- •Раздел 1. Основные понятия и определения та у 7
- •1.1 Цель и задачи дисциплины. Кибернетика. Основные понятия тау. Принципы автоматического регулирования 7
- •Раздел 7. Качество процессов управления 140
- •Раздел 8. Косвенные критерии качества 154
- •Раздел 9. Параметрический синтез типовых регуляторов 169
- •Раздел 10. Нелинейные системы. Общая характеристика нелинейных аср 173
- •Раздел 11. Системы регулирования при случайных воздействиях 214
- •Раздел 12. Дискретные (цифровые) автоматические системы регулирования (цаср) 245
- •Раздел 13. Анализ устойчивости дискретных систем 274
- •Раздел 14. Адаптивные системы 293
- •Решетчатые функции и z-преобразование
- •Определение z-преобразования
- •Основные свойства z-преобразования
- •Цифровые системы управления
- •Дискретное преобразование Лапласа и частотные характеристики
- •Связь между дискретным и непрерывным преобразованиями Лапласа и непрерывная модель дискретной системы
- •12.2 Уравнения элементов цифровой аср. Цифровой регулятор, идеальный импульсный элемент, формирующий фильтр, приведенная непрерывная часть Непрерывная модель дискретной системы
- •12.3 Преобразование сигналов идеальным импульсным элементом. Теорема Котельникова. Характеристики разомкнутых цаср
- •12.4 Частотные характеристики. Характеристики замкнутых систем Динамические характеристики
- •Раздел 13. Анализ устойчивости дискретных систем
- •13.1 Анализ устойчивости дискретных систем. Необходимые и достаточные условия устойчивости. Аналог критерия гурвица Характеристическое уравнение и основное условие устойчивости
- •Алгебраические критерии устойчивости
- •Исследование устойчивости, основанное на преобразовании единичного круга в левую полуплоскость
- •Критерий устойчивости Джури
- •13.2 Аналоги критериев михайлова, найквиста Частотный критерий устойчивости
- •Критерий Найквиста
- •13.3 Методы построения переходных процессов. Косвенные критерии качества
- •Показатели качества в переходном режиме
- •Прямые показатели качества
- •Косвенные показатели качества
- •Особенности переходного процесса дискретных систем
- •Раздел 1. Основные понятия и определения та у 7
- •1.1 Цель и задачи дисциплины. Кибернетика. Основные понятия тау. Принципы автоматического регулирования 7
- •Раздел 7. Качество процессов управления 140
- •Раздел 8. Косвенные критерии качества 154
- •Раздел 9. Параметрический синтез типовых регуляторов 169
- •Раздел 10. Нелинейные системы. Общая характеристика нелинейных аср 173
- •Раздел 11. Системы регулирования при случайных воздействиях 214
- •Раздел 12. Дискретные (цифровые) автоматические системы регулирования (цаср) 245
- •Раздел 13. Анализ устойчивости дискретных систем 274
- •Раздел 14. Адаптивные системы 293
- •13.4 Бесконечная степень устойчивости. Регуляторы Резвика, Смита Раздел 14. Адаптивные системы
- •14.1 Классификация адаптивных систем. Системы экспериментального регулирования (сэр). Сэр с запоминанием экстремума, градиентные сэр
- •Системы экстремального регулирования
- •Способ градиента
- •14.2 Системы с эталонной моделью. Алгоритмы идентификации Беспоисковые адаптивные системы управления
- •Идентификация и модель для получения оценки
- •Модель для получения оценки
11.3 Задачи анализа и синтеза аср при случайных воздействиях. Расчет дисперсии ошибки, параметрический синтез аср по минимуму дисперсии Задачи анализа и синтеза аср при случайных воздействиях
Так как устойчивость линейных систем является свойством системы и не зависит от характера воздействия, то устойчивость при случайных воздействиях определяется также, как и для детерминированных.
Качество систем при детерминированных воздействиях оценивается с помощью показателей качества, таких как tp, , T и т.д. При случайных воздействиях они теряют смысл, так как входные и выходные величины являются случайными функциями времени и при исследовании рассматривают не сами процессы, а их статистические свойства, т.е. определяют не мгновенные значения процессов, а их средние значения.
При случайных воздействиях ошибка системы (t) = x(t)-y(t) также является случайной величиной, при этом используют ее усредненное значение – среднюю квадратичную ошибку
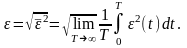 (11.3.1)
(11.3.1)
Эта ошибка используется для оценки точности или качества систем при случайных воздействиях.
Недостатки средней квадратичной ошибки:
1.Она обеспечивает минимум не мгновенного, а среднего значения, при этом мгновенное значение может быть недопустимо большим.
2. Она недооценивает малые ошибки и придает чрезмерное значение большим ошибкам, так как ее значение возводится в квадрат.
Синтез оптимальных передаточных функций САУ при случайных воздействиях
Если на входе системы помимо управляющего есть и возмущающее воздействие (помеха), то ошибка такой системы состоит из двух составляющих. Часто оказывается, что стремление уменьшить одну составляющую приводит к увеличению второй и наоборот. Задача синтеза и состоит в том, чтобы обеспечить минимально возможную сумму обеих составляющих.
Возможны несколько способов решения задачи синтеза. Первый и наиболее простой применим, если уже известна структура системы. В этом случае необходимо, используя выше приведенные выражения определить СКО как функцию варьируемых параметров системы и обычным методом определить их значения, дающие минимум ошибки. Еще один способ применим когда полезный сигнал имеет более низкочастотный спектр, чем помеха (рис.11.3.1).
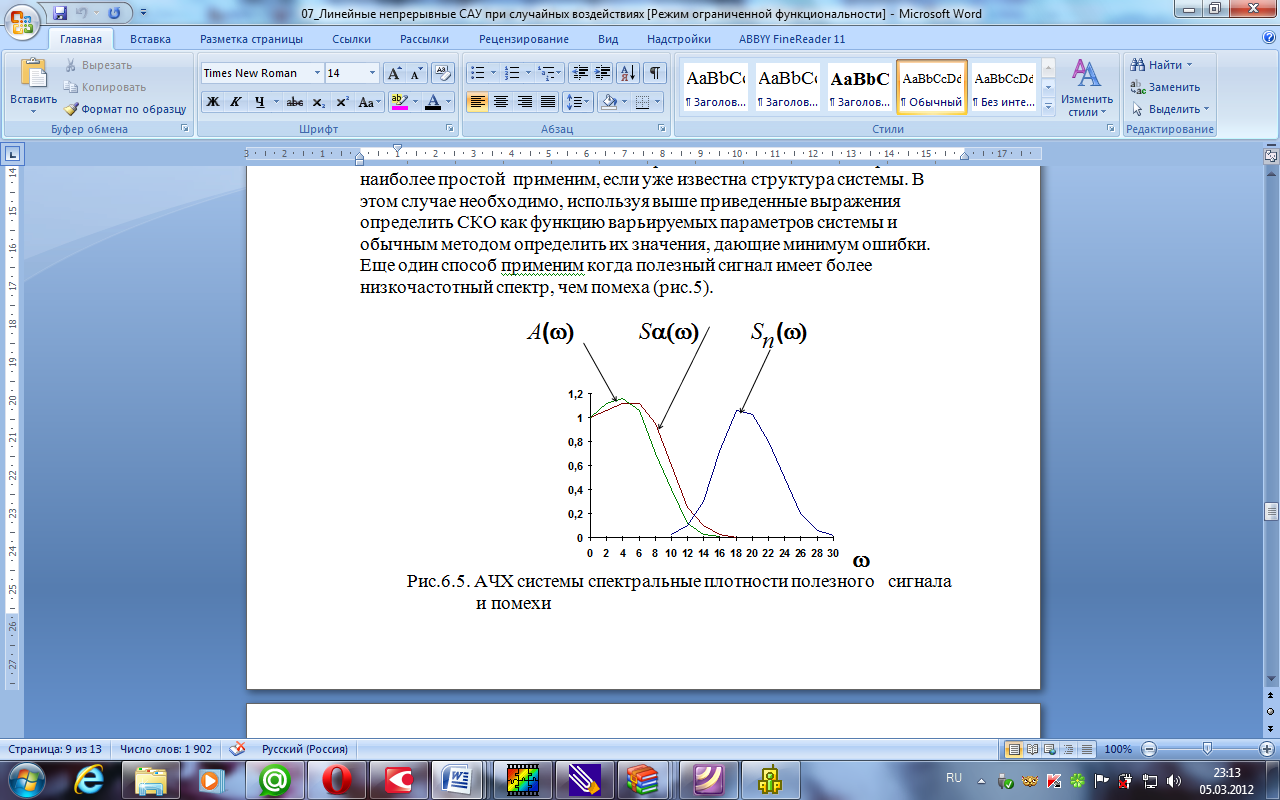
Рис.11.3.1. АЧХ системы спектральные плотности полезного сигнала и помехи
В этом случае полоса пропускания системы должна быть выбрана достаточно широкой для обеспечения необходимой точности воспроизведения полезного сигнала, но такой ширины, чтобы полностью отфильтровать помехи.
В наиболее общем случае, когда спектры полезного сигнала и помехи накладываются друг на друга систему строят так, чтобы ее частотная характеристика максимально приближалась к спектральной характеристике полезного сигнала.
Рассмотрим методику определения оптимальной передаточной функции по критерию минимума СКО, когда структура системы неизвестна, а известна только передаточная функция неизменяемой части.
При
определении оптимальной частотной
характеристики замкнутой САУ
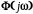 по критерию минимума СКО между идеальным
сигналом
по критерию минимума СКО между идеальным
сигналом
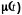 и оптимальным сигналом
и оптимальным сигналом
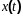 ,
предположим, что:
,
предположим, что:
1)
идеальная частотная характеристика
 или идеальная функция веса
или идеальная функция веса
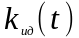 известны;
известны;
2)
полезный сигнал
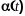 и помеха
и помеха
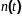 являются стационарными эргодическими
случайными процессами с нулевым
математическим ожиданием и их
корреляционные функции и спектральные
плотности известны;
являются стационарными эргодическими
случайными процессами с нулевым
математическим ожиданием и их
корреляционные функции и спектральные
плотности известны;
3) на время переходного процесса ограничения не накладываются, т.е. решение ищется в классе систем с “ бесконечной памятью”.
Схема постановки задачи приведена на рисунке 11.3.2.
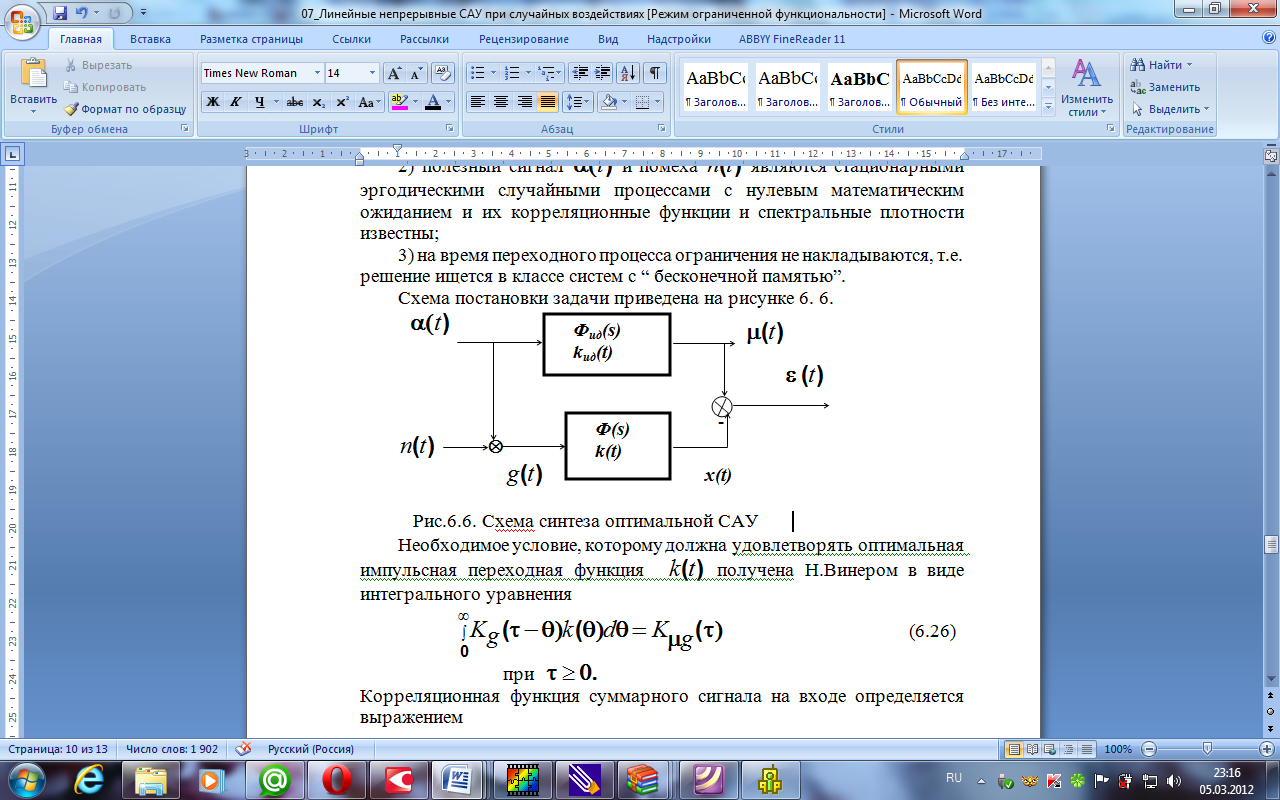
Рис.11.3.2. Cхема синтеза оптимальной САУ
Необходимое
условие, которому должна удовлетворять
оптимальная импульсная переходная
функция
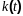 получена Н.Винером в виде интегрального
уравнения
получена Н.Винером в виде интегрального
уравнения
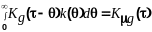 (11.3.2)
(11.3.2)
при
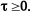
Корреляционная функция суммарного сигнала на входе определяется выражением
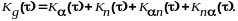
Условие
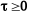 отражает принцип физической осуществимости
системы. Если полезный сигнал и помеха
некоррелированы, то
отражает принцип физической осуществимости
системы. Если полезный сигнал и помеха
некоррелированы, то
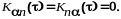
Уравнение (11.3.2) можно преобразовать к виду
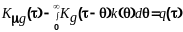 ,
(11.3.3)
,
(11.3.3)
где
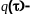 некоторая
функция, равная нулю при
Это условие приводит к тому, что функция
некоторая
функция, равная нулю при
Это условие приводит к тому, что функция
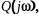 связанная с
связанная с
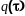 преобразованием Фурье, не будет
содержать полюсов в верхней полуплоскости
плоскости
преобразованием Фурье, не будет
содержать полюсов в верхней полуплоскости
плоскости
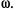 Преобразование Фурье дает возможность
перейти к спектральным плотностям.
Преобразование Фурье дает возможность
перейти к спектральным плотностям.
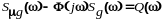 (11.3.4)
(11.3.4)
Предположим, что спектральная плотность входного сигнала имеет дробно-рациональный вид и может быть представлена в виде
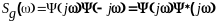 (11.3.5)
(11.3.5)
Здесь
 имеет все нули и полюсы в верхней
полуплоскости, а
имеет все нули и полюсы в верхней
полуплоскости, а
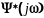 -в
нижней полуплоскости плоскости
Разделим (11.3.4)
на
-в
нижней полуплоскости плоскости
Разделим (11.3.4)
на
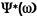 и получим
и получим
 (11.3.6)
(11.3.6)
Дробь в левой части выражения (11.3.6) можно преобразовать к виду суммы
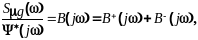 причем
причем
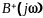 имеет все нули и полюсы только в верхней
полуплоскости, а
имеет все нули и полюсы только в верхней
полуплоскости, а
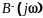 -только
в нижней полуплоскости плоскости .
С учетом этого выражение (11.3.6)
преобразуем к виду
-только
в нижней полуплоскости плоскости .
С учетом этого выражение (11.3.6)
преобразуем к виду
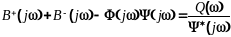
Последнее
выражение справедливо для всей плоскости
.
Однако, поскольку необходимо выполнение
условия физической реализуемости
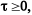 то решение ищется только в верхней
полуплоскости и указанное выражение
принимает вид
то решение ищется только в верхней
полуплоскости и указанное выражение
принимает вид
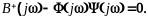
Отсюда для амплитудно-фазовой характеристики замкнутой САУ получим
 (11.3.7)
(11.3.7)
Передаточная
функция замкнутой САУ
 По этой передаточной функции определяется
передаточная функция разомкнутой
системы, а затем, с учетом известной
передаточной функции неизменяемой
части, находится передаточная функция
корректирующего устройства.
По этой передаточной функции определяется
передаточная функция разомкнутой
системы, а затем, с учетом известной
передаточной функции неизменяемой
части, находится передаточная функция
корректирующего устройства.
Пример 11.3.1
Полезный сигнал и помеха заданы своими корреляционными функциями:
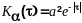 ;
;

Полезный
сигнал и помеха не коррелированы.
Идеальная передаточная функция
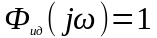 ,т.е.
должна быть решена задача оптимальной
фильтрации.
,т.е.
должна быть решена задача оптимальной
фильтрации.
Прежде всего определим спектральные плотности.
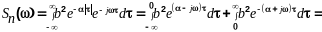
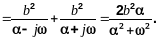
Аналогично получим
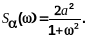
Далее процесс решения задачи Винера состоит из следующих операций:
1.Вычислим
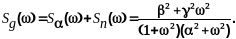
Здесь
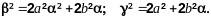
Разложим эту функцию на комплексно-сопряженные множители
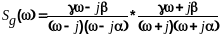
Отсюда
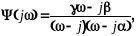
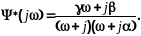
2. Вычислим взаимную спектральную плотность
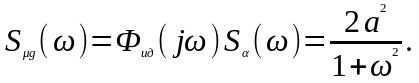 Ф
Ф
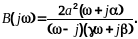
3.
Определим функцию
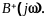
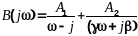
Приведя к общему знаменателю и приравнивая числители этого и предыдущего выражений, получим систему уравнений, из решения которой будем иметь
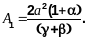
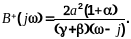
4. Вычислим частотную характеристику оптимальной системы