1.2. Погрешности измерений

Результаты измерения физической величины дают лишь приближенное ее значение. Отклонение результа­та измерения от истинного значения измеряемой вели­чины называют погрешностью измерения. Различают абсолютную и относительную погрешности измерения.

Абсолютная погрешность измерения ДЛ равна разно­сти между результатом измерения А_х и истинным значе­нием измеренной величины А:

АЛ = А_х—А.

Относительная погрешность измерения 6а представ­ляет собой отношение абсолютной погрешности измере­ния к истинному значению измеряемой величины, выра­женное в процентах:

б = М ЮО. ^л А

Тан как истинное значение измеряемой величины неиз­вестно, вместо истинного значения используют так на­зываемое действительное значение, под которым понима­ют значение измеряемой величины, найденное экспери­ментальным путем и настолько приближающееся к истинному значению, что может быть использовано вме­сто него. По этой причине на практике значение погреш­ности измерения можно оценить только приближенно. Погрешности считаются положительными, если резуль­тат измерения превышает действительное значение.

Для получения действительного значения измеряемой величины в ряде случаев учитывают погрешности средств измерений путем введения поправок. Поправкой называется абсолютная погрешность, взятая с обратным знаком.

Пример. Результат измерения тока 49,9 А, а его действи­тельное значение /=50,0 А.

Абсолютная погрешность измерения

М = /_ж —/ = 49,9 — 50,0 ==—0,1 А.

Относительная погрешность измерения

6, = — 100 =— —100 =— 0,2%.

/ 50

Поправка, которую следует ввести в результат измерения, рав­на—Д/= 0,1 А.

Погрешности измерений имеют систематическую и случайную составляющие, которые называют также сис­тематической и случайной погрешностями.

Под систематическими погрешностями понимают по­грешности, остающиеся постоянными или закономерно изменяющиеся при повторных измерениях одной и той же величины. Систематические погрешности могут быть определены и устранены путем введения соответствую­щих поправок. Примером систематических погрешностей является погрешность градуировки прибора, т. е. ошибки в положении делений, нанесенных на шкалу прибо­ра. Влияние внешних факторов (например, коле­бания температуры, напряжения питания) на средства измерения также вызывает появление систематических погрешностей.

17

Случайными называются погрешности, изменяющие­ся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности нельзя ис­ключить опытным путем. Они происходят от влияния на

2—970

результат измерения причин случайного характера, ия- г.ример погрешность or трения в опорах измерительных приборов.

Уменьшение влияния случайных погрешностей на ре­зультат измерений достигается путем многократных измерений величины в одинаковых условиях. Если при­нять, что систематические погрешности близки к нулю, го наиболее достоверное значение, которое можно при­писать измеряемой величине на основании ряда измере­ний, есть среднее арифметическое из полученных значе­ний, определяемое как

Л_ср = (а_г + а₂ -! Ь а_п)'п,

где а_и 0.2,..., а_п — результаты отдельных измерений; п — число измерений.

Для опенки точности результата измерений необхо­димо знать закон распределения случайных погрешно­стей.

В практике электрических измерений одним из наи­более распространенных законов распределения случай­ных погрешностей является нормальный закон (Гаусса).

Математическое выражение нормального закона име­ет вид:

р(6) = —^-«Г^, (И)

а V 2я

где р(б) — плотность вероятности случайной погрешно­сти б; а — среднее квадратическое отклонение.

Как следует из (1.1), при 6 = 0

р (6) = 1/ст УЪг.

Среднее квадратическое отклонение может быть вы­ражено через случайные отклонения результатов наблю­дения р:

о к ]/(р2 + р| Ч Ь Р²_п)!{п— ⁵).

где р1=а,— Л_ср; р₂=й₂—Л_ср; р_п=а_п—А_ф.

Характер кривых, описываемых уравнением (1.1) для двух значений а, показан на рис. 1.1. Из этих кривых видно, что чем меньше а, тем чаще встречаются малые случайные погрешности, т. е. тем точнее выполнены из­мерения. Кривые симметричны относительно оси орди­нат, так как положительные и отрицательные погрешно­сти встречаются одинаково часто.

Вероятность появления погрешности со значениями от 6i до 62 определяется площадью заштрихованного участка на рис. 1.1. При нормальном законе распреде­ления вероятность появления случайных погрешностей в интервале от 8i до 82 вычисляется как определенный интеграл от функции р(6):

е,

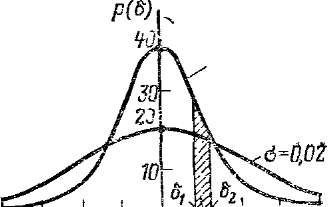
б=0Ш

Рис. 1 1. Нормальный закон распределения случайных по­грешностей.

Ъо¥цоз 0,02 тот о,ог о,озо,оч-

Я= \p(8)d8.

Значения этого интеграла вычислены для различных пределов (интервалов ±А6) и сведены в таблицы, при­веденные в математических справочниках. Интеграл, вы­численный для пределов от 61=—оо до 62= + °°. равен единице, т. е. вероятность появления случайной по­грешности в интервале от —то до оо равна единице. Это естественно, так как все погрешности имеют конеч­ные значения.

Как указывалось ранее, среднее арифметическое ря­да измерений Л_ср является лишь наиболее достоверным

значением измеряемой величины. Точность результата измерения Л_ср можно оценнть с помощью средней квад- ратической и вероятной погрешностей. Если случайные погрешности распределены по нормальному закону, то согласно теории погрешностей средняя квадратическая погрешность среднего арифметического значения равна:

/

VI

п (п — 1)

Р?"

-р1-

Из данного выражения видно, что увеличение коли­чества повторных измерений п приводит к уменьшению средней квадратической погрешности сг_А результата из­мерений.

19

Если известен закон распределения случайных по­грешностей, можно определить вероятность появления погрешности б, не выходящей за некоторые принятые границы. Этот интервал называют доверительным интер-

2*

валом, а характеризующую его вероятность — довери­тельной вероятностью.

При нормальном законе распределения по таблице интеграла вероятностей можно определить значения доверительных интервалов. При увеличении доверитель­ных интервалов значения доверительных вероятностей возрастают, стремясь к пределу, равному единице. На­пример, для доверительного интервала от 6i=—а до 8г=+сг доверительная вероятность Р равна 0,68. Следо­вательно, вероятность того, что случайная погрешность не превышает среднего квадратического значения, равна 0,68. Так как вероятность появления случайной погреш­ности для доверительного интервала от 6i =—оо до б2=+оо равна единице, то вероятность появления по­грешности по абсолютному значению, превышающей о, равна 1—0,68 — 0,32, т. е. примерно только одно из трех измерений будет иметь погрешность, большую а.

Для доверительного интервала от —3 а до + 3 а дове­рительная вероятность равна 0,9973. Вероятность появ­ления погрешности, большей За, равна 1—0,9973= =0,0027 л; 1/370. Такая доверительная вероятность означает, что из 370 случайных погрешностей только одна погрешность по абсолютному значению будет боль­ше 3 а. Поэтому значение 3 а считается максимально возможной случайной погрешностью. Погрешности, большие 3 а, считаются промахами и при обработке ре­зультатов измерений не учитываются.

Как указывалось, для оценки точности результата из­мерения можно воспользоваться вероятной погрешно­стью.

Вероятной погрешностью называется такая погреш­ность, относительно которой при повторных измерениях какой-либо величины одна половина случайных погреш­ностей по абсолютному значению меньше вероятной погрешности, а другая — больше ее. Из данного опреде­ления следует, что вероятная погрешность равна дове­рительному интервалу, при котором доверительная ве­роятность Р=0,5.

Вероятная погрешность результата измерений, т. е. среднего арифметического значения, при нормальном за­коне распределения случайных погрешностей равна:

_2 3

2

л/ ^pi^+p^

У п(.

ti (п — 1)

Следует отметить, что указанный способ определения доверительных интервалов справедлив только при боль­шом количестве измерений («>20+30). На практике чаще всего значение е_А приходится определять по ре­зультатам сравнительно небольшого количества измере­ний. В этом случае при нормальном законе распределе­ния для определения доверительного интервала нужно пользоваться коэффициентами Стьюдента /„, которые зависят от задаваемой доверительной вероятности Р и количества измерений п (табл. 1.3).

Таблица 1.3. Коэффициенты Стьюдента

	р
п
	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99	0,959
2	1,00	1,38	2,0	3,1	6,3	12,7	31,8	63,7	636,6
3	0,82	1,06	1,3	1,9	2,9	4,3	7,0	9,9	31,6
4	0,77	0,98	1,3	1,6	2,4	3,2	4,5	5,8	12,9
5	0,74	0,94	1,2	1,5	2,1	2,8	3,7	4,6	8,6
6	0,73	0,92	1,2	1,4	2,0	2,6	3,4	4,0	6,9
7	0,72	0,90	1,2	1,4	1,9	2,4	3,1	3,7	6,0
8	0,71	0,90	1,1	1,4	1,9	2,4	3,0	3,5	5,4
9	0,71	0,90	1,1	1,4	1,9	2,3	2,9	3,4	5,0
10	0,70	0,88	1,1	1,4	1,8	2,3	2,8	3,3	4,8
15	0,69	0,87	1,1	1,3	1,8	2,1	2,6	3,0	4,1
20	0,69	0,86	1,1	1,3	1,7	2,1	2,5	2,9	3,9
30	0,68	0,85	1,1	1,3	1,7	2,0	2,5	2,8	3,7

Для определения доверительного интервала среднюю квадратическую погрешность о_А надо умножить на ко­эффициент Стьюдента. Окончательный результат изме­рения можно записать так:

A = A_cp±t_na_A.

Пример. Искомое сопротивление было измерено 8 раз, при этом получены результаты: Ri= 116,2 Ом; «₂= 118,2 Ом; R₃= 118,5 Ом; #4=117,0 Ом; #₅=118,2 Ом; /?₆= 118,4 Ом; «7=117,8 Ом; «₈= = 118,1 Ом.

Наиболее вероятное среднее значение сопротивления

g =

116,2 -f 118,2 + 118,5 + 117,0+ 118,2-h 118,4 + 117,8+ 118,1

8 ⁼ = 117,8 Ом.

Остаточные погрешности отдельных измерений pi —Rep— =—1,6 Ом; р2=0,4 Ом; р₃=0,7 Ом, р₄ = —0,8 Ом; р₅=0,4 Ом; р₆= =0,6 Ом; р₇=0,0 Ом; р₈=0,3 Ом

^ = ]

Средняя квадратическая погрешность результата измерения

р2 + р] + ---+р!

ri {п— 1)

6)2 о + 0,72 + (— 0,8)² 4-0,42 -р

- 0,6² -f- 0,0² + 0,3² —¹ '— = 0,29 Ом.

Нужно определить интервал, в котором находится значение из­меряемого сопротивления, с доверительной вероятностью Р=0,99. По табл. 1.3 находим для Р=0,99 и п=8 коэффициент /«=3,5, то­гда результат равен: ^=117,8= 3,5X 0,29 0м=117,8±1,0 Ом.

Для определения вероятной погрешности результата измерения найдем из габл 1.3 зпачение коэффициента Стьюдента для довери­тельной вероятности Р=0,5 и п=8 Коэффициент <„=0,71, тогда ве­роятная погрешность результата измерения е.д=0,71-0,29=0,2 Ом.

Определим погрешность результата измерения при косвенных измерениях.

Допустим, что искомая величина А является извест­ной функцией полученных прямыми измерениями вспо­могательных величин В и С:

A = F(B,C). (1.2)

Требуется определить погрешность величины А, ес­ли известны погрешности величин В и С.

Прологарифмируем и продифференцируем соотноше­ние (1.2), положив В я С переменными. В результате найдем:

Ad С

где Fi(B, С) и F₂(B, С)—функции переменных В и С.

Заменив дифференциалы dA, dB и dC малыми при­ращениями, которые можно рассматривать как абсолют­ные погрешности, получим:

м = Г_1(В,С)^--\-Г,{В, С)^, (1.3)

или

⁶Л = ^Fl (^В> ^С) ⁶£ + ^F1 (^В> ^С) ⁶С>

где 6_Л=ДЛ/Л; 6в=ДВ/В; 6с=ДС/С — относительные погрешности величин А, В, С.

Уравнение (1.3) дает возможность определить погрешность искомой величины А, зная погрешности вели­чин В и С. Так как в большинстве случаев знак погреш­ностей бв и 6с неизвестен, то при определении наиболь­шей возможной погрешности всегда следует рассматри­вать неблагоприятный случай, при котором слагаемые Fi(B, С)6_В и F_Z(B, С)8с имеют одинаковые знаки.

Определим, например, погрешность измерения вели­чины Л, которая связана с величинами В и С, найден­ными прямыми измерениями, соотношением

Л=В" С^!п,

где п и т — показатели степени, которые могут быть целыми, дробными, положительными или отрицатель­ными.

Взяв логарифмы правой и левой частей уравнения, получим:

In Л = п In В + m \п С.

Продифференцировав написанное выражение, най­дем:

&А dB С

—- = п \- т -

Л В с

Заменив дифференциалы dA, dB и dC малыми при­ращениями, запишем:

ДЛ ДВ , ДС

— —п Ь т —,

А ВС'

или

8_л=п8_в + т6_Сг

где бл=ДЛ/Л; бв=ДВ/В; бс=ДС/С — относительные погрешности величин А, В, С.

Пример. Пусть п=—2, т=3, 6в=±0,5%, 6_С = ±0,2%. В этом случае наибольшая возможная относительная погрешность измере­ния величины Л составит:

&Атах =± (I л«в | + I |) =±(2-0,5 + 3-0,2) = = ±(1+0,6) =±1,6%.

Определим наибольшую возможную относительную погрешность величины Л, если она связана с величина­ми В, С и D зависимостью вида

A = B+C — D.

Прологарифмировав и продифференцировав данное выражение и заменив дифференциалы dA, йВ и dC ма­лыми приращениями, найдем:

б = — = ^Ай + ^АС — ^А~~ A B + C — D "

Если B + CtzD, то погрешность величины А может быть очень большой, несмотря на сравнительно малые погрешности величин В, С и D.