2. Задания 2 и 3 по теме «Неопределенный интеграл, определенный интеграл и его применение для вычисления площади фигуры» Краткие теоретические сведения
Понятие неопределенного интеграла
Функция F(x)
называется первообразной для функции
f(x)
на некотором промежутке Х, если для
любого элемента
выполняется
равенство F'(x) = f(x).
Если F(x) — одна из первообразных для функции f(x) на промежутке Х, то всякую другую первообразную Ф(х) на промежутке Х можно представить в виде Ф(х) = F(x) + с, где с — постоянная величина.
Неопределенным
интегралом от функции f(x)
называется множество всех ее первообразных,
т. е.
.
При этом f(x)
— подынтегральная функция, f(x)dx
— подынтегральное выражение,
знак
неопределенного интеграла, х —
переменная интегрирования.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Свойства неопределенного интеграла:
1. 
2. 
3. 
4. 
где
с — постоянная величина.
5. 
.
6. Если
=
F(x) + c и
— дифференцируемая функция, то
=
F(и) + c.
Таблица основных неопределенных интегралов:
1. 
2. 
3. 
4.
.
5. 
.
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
Интегрирование методом замены переменной и по частям
Метод замены переменной проводится по формуле
где
х =
—
некоторая дифференцируемая функция.
Если и = и(х), v = v(x) — некоторые дифференцируемые функции, то справедлива формула интегрирования по частям
Интегрирование простейших рациональных дробей
Интегрирование проводят в зависимости от типа простейшей рациональной дроби.
1. 
(А,
а
— постоянные действительные числа) —
простейшая рациональная дробь первого
типа.
Пример.
=
=
=
= =
=
.
2. 
(А, а, т — постоянные числа,
,
)
— простейшая рациональная дробь второго
типа.
Пример.
=
=
=
=
=
=
=
.
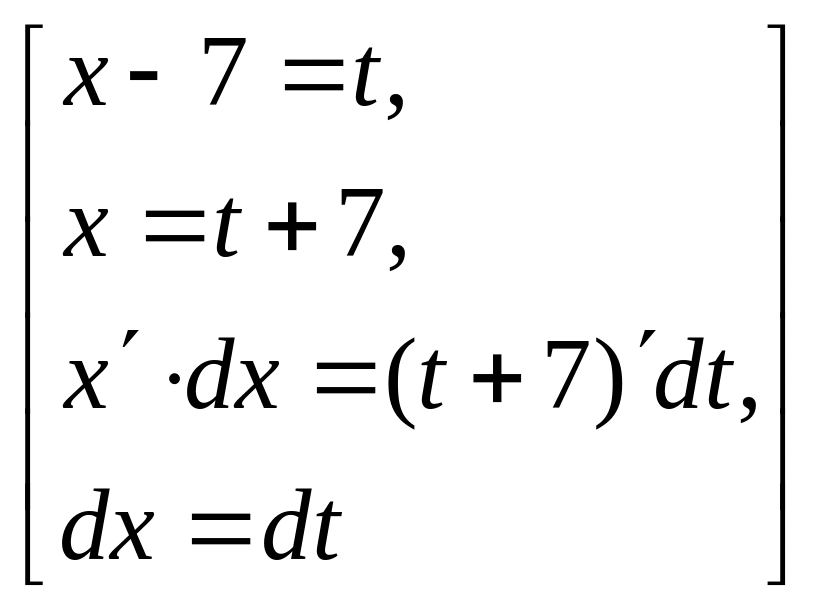3. 
(М, N, p, q — постоянные
числа, М, N, p, q
,
х2 + рх + q не
имеет действительных корней) — простейшая
рациональная дробь третьего типа.
Пример.
=
+
=
=
dx
+
=
dx
–
·
·
+ 5 · 
=
=
=
–
=
–
=
=d(x + 2)
= (x + 2)'dx = dx
=
–
=
·
·
–
arctg(x + 2) + c.
4. 
(М, N, р, q — постоянные
числа, М, N, р, q
,
,
;
х2 + рх + q не
имеет действительных корней) — простейшая
рациональная дробь четвертого типа.
Интеграл от этой дроби считается с помощью рекуррентных формул, позволяющих уменьшить число т до 1.
Интегрирование правильных и неправильных рациональных дробей
Рациональная дробь
(Qn(x), Qm(x)
— некоторые многочлены степеней n
и m соответственно) называется
правильной, если
,
и неправильной в противном случае
(если
).
Для интегрирования правильной дроби ее предварительно раскладывают на простейшие дроби. Для этого многочлен Qn(x) разлагают на неприводимые множители. Общий вид такого разложения следующий:
=
+
+
… +
+
+
… +
+
… +
+
+
+
+…+
,
где А1, А2, …, Аk, В1, В2, …, Вr , М1, М2, …, Мs , N1, N2, …, Ns — некоторые неопределенные действительные коэффициенты, которые следует еще определить.
Интегрирование неправильной рациональной дроби сводят к интегрированию правильной рациональной дроби выделением из первой целой части.
Интегрирование некоторых иррациональных функций
Если f(x)
=
,
то для ее интегрирования применяют
подстановку
,
где п = НОК (n1, …, nk).
Пример.
=
=
=
=
=
–
+
+
с =
=
–
+
+
с
=
–
·
+
+
+
с.
Определенный интеграл и его основные свойства
Пусть на отрезке
a,b
определена функция у = f(x).
Разобьем этот отрезок на п частей
точками
=
b. На каждом отрезке хi–1;
xi
возьмем произвольную точку
(i
= 1, 2,…, п) и составим сумму
,
где
.
Сумма
называется интегральной суммой функции
f(x)
на отрезке a,b,
а ее предел при
,
если он существует и конечен, называется
определенным интегралом от функции
у = f(x)
в пределах от а до b
и обозначается следующим образом:
.
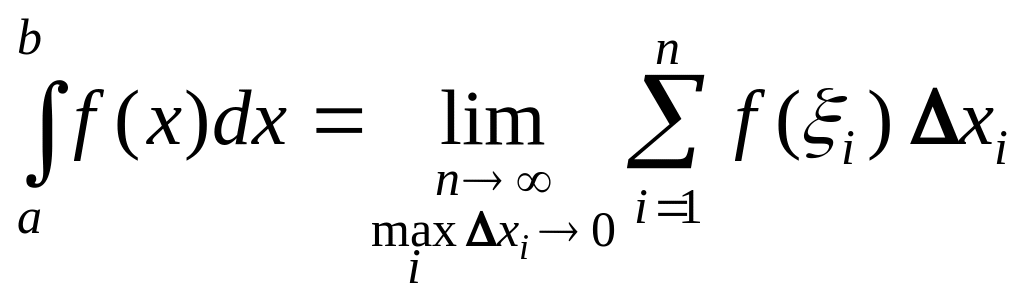В этом случае функция у = f(x) называется интегрируемой на отрезке a,b.
Среди многих экономических интерпретаций определенного интеграла отметим следующую:
равен объему
производства от момента времени t
при условии, что f(t)
— производительность труда в момент
времени t.
Определенный интеграл имеет следующие свойства:
1. 
.
2. 
=
+
–
.
3. 
.
Формула Ньютона-Лейбница и интегрирование по частям
Если функция у = f(x) непрерывна на отрезке a,b и F(x) — одна из первообразных для f(x), то справедлива формула Ньютона-Лейбница
.
Если и = и(х), v = v(x) — дифференцируемые функции на отрезке a,b, то
.
Замена переменной в определенном интеграле
Если
— функция, непрерывная вместе со своей
производной
на отрезке 
,
,
,
то
.
Вычисление площадей плоских фигур при помощи определенного интеграла
Площадь фигуры, ограниченной кривыми (рис. 18) у = f1(x), у = = f2(x) (f1(x) f2(x)) и прямыми х = а, х = b, находится по формуле
.
|
Рис. 18 |
