4.13. Формула Тейлора7

Пусть Р_n(х) — многочлен степени n. Запишем его в виде разложения по степеням разности х – , где R:

(4.13.1)

Равенство (13.1) должно выполняться для любых значений х: слева записан многочлен и справа, если раскрыть скобки и привести подобные члены, должен получаться он же. Коэффициенты мы считаем неизвестными. Оказывается, что их можно легко вычислить с помощью производных многочлена Р_n (х). Для этой цели сначала положим в (4.13.1) х = :

х =  = Р_n ( ).

Для нахождения продифференцируем равенство (4.13.1) и положим затем х = :

(4.13.2)

х =  = Р_n' ( ).

Для вычисления продифференцируем (4.13.2) и положим х = :

(4.13.3)

Далее поступаем аналогично:

следовательно,

(нетрудно видеть, что ).

Полученные формулы для коэффициентов можно обобщить следующим образом:

(4.13.4)

причем ,  0! = 1! = 1. Величины (4.13.4) называются коэффициентами Тейлора для многочлена в окрестности точки .

С помощью (4.13.1), (4.13.4) получаем следующее представление многочлена:

(4.13.5)

Выражение (4.13.5) называется формулой Тейлора для многочлена.

Пусть теперь — произвольная функция, дифференцируемая нужное количество раз. Для нее построим такой многочлен Тейлора , что

(4.13.6)

т. е. положим

(4.13.7)

Функция и многочлен будут близкими в окрестности точки и тем ближе, чем выше n. На рисунке схематически показаны графики нескольких многочленов для n = 0, 1, 2.

Многочлен дает довольно грубое приближение функции — он пересекает ее график. Функция y=P₁(x) выражает прямую, касающуюся кривой . Линии у=Р₂(х) и имеют равные радиусы кривизны при х = и т.д.

Условимся говорить, что кривые и имеют соприкосновение порядка n в точке , если ,

Тогда кривая и многочлен (4.13.6) в силу (4.13.7) имеют в точке соприкосновение порядка не ниже n.

Несмотря на близость функций f (x) и Р_n (х) они все же различаются:

f (x) – Р_n (х) = R_n (х) .

Величина R_n (х) выражает разницу между f (x) и Р_n (х) и может рассматриваться как погрешность при замене f (x) на Р_n (х).

Очевидно, что

f (x) = Р_n (х) + R_n (х) ,

или

(4.13.8)

Выражение (4.13.8) называется формулой Тейлора для функции f (x), R_n (х) называется остаточным членом формулы Тейлора, а величины

(4.13.9)

называются коэффициентами Тейлора для функции f (x).

Формулу Тейлора (4.13.8) можно записать также с помощью дифференциалов

(4.3.10)

Вопросы

1. В каком случае R_n (х) = 0?

2. Какие требования следует предъявить к функции f (x) с тем, чтобы для нее можно было записать формулу Тейлора?

4.14. Остаточный член формулы Тейлора в форме Лагранжа

Исходя из соображений, приведенных в предыдущем пункте, можно предположить, что R_n (х) с ростом n убывает. Однако пока неизвестно, как оценивать величину R_n (х). Для R_n (х) предложено несколько различных выражений, но чаще других используется выражение, найденное Лагранжем.

Будем искать R_n (х) в виде, сходном со следующим членом тейлоровского разложения:

(4.14.1)

где Q_n(x) — неизвестная функция.

Зафиксируем х и введем вспомогательную функцию

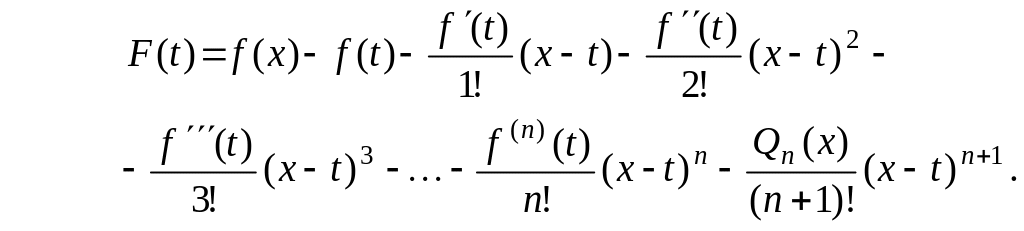
Пока не ясно, зачем потребовалось придумывать столь вычурное выражение. Однако это выясняется немедленно.

В самом деле,

F(x)=F( )=0;

Таким образом, F(х) — функция, удовлетворяющая условиям теоремы Ролля.

Согласно теореме Ролля существует точка ( , x), в которой F'() = 0, т.е.

(4.14.2)

(теперь ясно, сколь дальновидно была сконструирована функция F(t)).

Подставляя (4.14.2) в (4.14.1), получаем искомое выражение остаточного члена в форме Лагранжа:

(4.14.3)

Очевидно, что если при ( , x), то

. (4.14.4)

Выражение (4.14.4) иногда называют остаточным членом в форме Пеано⁸ .

Погрешность, возникающую при замене данной функции соответствующим ей многочленом Тейлора, оценивают с помощью формулы (4.14.3).