4.25. Понятие о задачах нелинейного и целочисленного программирования

Задача нелинейного программирования является непо­средственным обобщением задачи линейного программирования (см. (4.24.4) – (4.24.6)): найти глобальный экстремум функции

(4.25.1)

при ограничениях

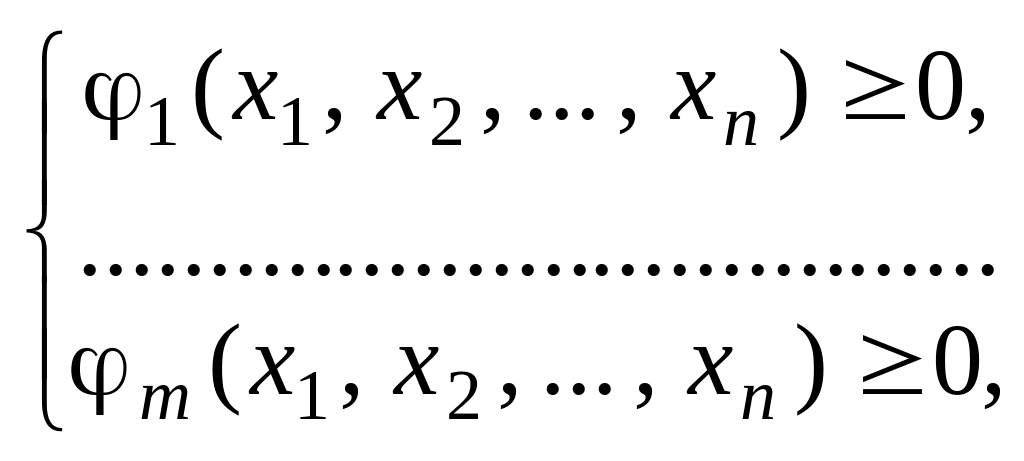(4.25.2)

(4.25.3)

Следует заметить, что здесь уже не выполняются отмеченные для случая задачи линейного программирования осо­бые свойства, и экстремум целевой функции может дости­гаться внутри области [A], определяемой ограничениями (4.25.2), (4.25.3). Общего эффективного алгоритма решения задачи (4.25.1) – (4.25.3) не существует, однако для важных част­ных случаев такие алгоритмы имеются (квадратичное про­граммирование, выпуклое программирование – см. цитированную книгу Т. Л. Кузина).

В некоторых слу­чаях переменные x₁, х₂, ... , x_п не могут принимать дробных значений (например, когда они выражают количества неделимых изделий). В этом случае задача линейного программирования (4.24.4) – (4.24.6) превращается в задачу целочисленного про­грам­мирования. Для решения такой задачи разработаны специальные алгоритмы. Заметим, что простое округление в задаче линейного программирования не всегда приво­дит к оптимальному решению соответствую-щей задачи целочисленного про­граммирования (см. рисунок).

4.26. Дифференциал и производная вектор-функции скалярного аргумента

Рассмотрим вектор-функцию одной переменной, отображающую R в :

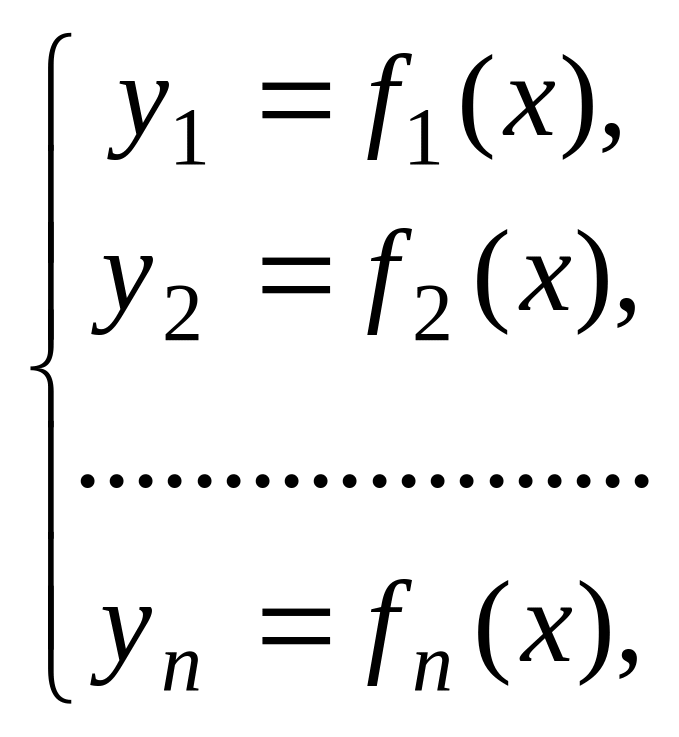
или короче

П онятие предела вектор-функции скалярного аргумента вводится обычным образом:

Нетрудно убедиться в том, что условие

равносильно существованию n «скалярных» пределов

(проверить самостоятельно).

Вектор-функция называется непрерывной в точке , если

Вектор-функция скалярного аргумента называется дифференцируемой,

если ее приращение можно представить в виде

(4.26.1)

где – линейная относительно х вектор-функция; ( х) – вектор-функция, для которой

. (4.26.2)

Очевидно, что

(4.26.3)

где

Умножим обе части равенства (4.26.1) на х^–1 и перейдем к пределу при х0. Тогда в силу (4.26.2), (4.26.3) получим

Этот предел называется производной вектор-функции. Поэтому, как и для любого отображения, имеем

(4.26.4)

Теперь дифференциал (4.26.3) можно записать в виде

.

Так как, в частности, при получается dх=х, то

(4.26.5)

Согласно (4.26.4) легко устанавливается правило для вы­числения координат производной вектор-функции скалярного аргумента:

Таким образом, для вычисления производной вектор-функции достаточно составить вектор из производ­ных всех ее координат.

Уже отмечалось, что при п = 2 вектор-функция скалярного аргумента выражает параметрическое уравнение плоской, а при n = 3 – пространственной кривой.

Из рисунка ясно, что при х0 вектор поворачивается и дает в пределе вектор , направленный по касательной к кривой.

В механике для описания движения точки используют вектор-функцию вида , где t – время, – радиус-вектор движущейся точки. При этом производная выражает вектор скорости точки. Действительно, производная направлена по касательной к траектории движения, а модуль производной

есть не что иное, как модуль скорости.

Аналогично можно найти ускорение движущейся точки

.

П р и м е р ы

1. Движение точки представляет собой суперпозицию двух ортогональных гармонических колебаний асost и bsint. Требуется найти наибольшее и наименьшее значения модуля скорости точки.

Полагая, что a > b > 0,  > 0, приходим к искомому результату:

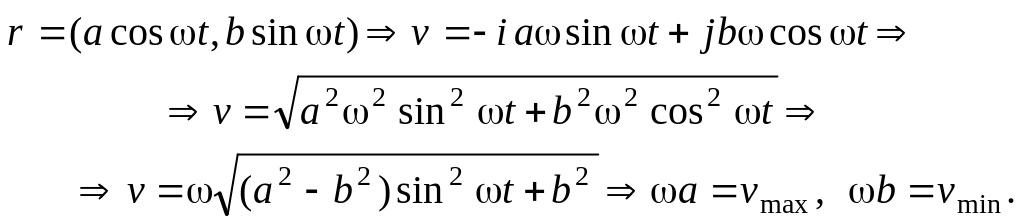
2. Показать, что кривые и пересекаются и определить угол между кривыми в точке их пересечения.

Установим вначале факт пересечения кривых:

Найдем производные вектор-функций:

Затем вычислим значения производных в точке пересечения кривых

.

Наконец, определяем косинус угла между этими векторами:

2. Вывести формулу для вычисления производной векторного произведения .

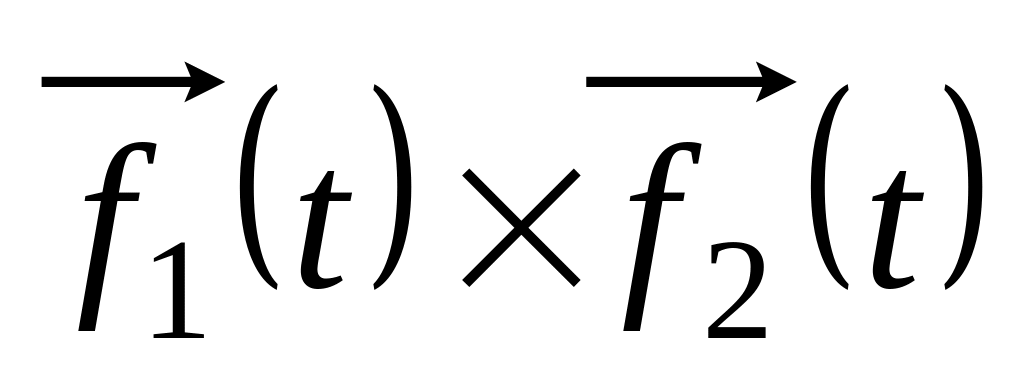Обозначив , имеем

откуда после умножения на t ^–1 и предельного перехода при t получаем искомую формулу